Лекция 4: Параллельные и сетевые технологии решения задач линейного программирования
Пример применения параллельной процедуры прямого перебора
Решим ту же задачу (2), подойдя формально, по правилу, пригодному для любой размерности пространства.
Исходная система уравнений действительных или потенциальных плоскостей — граней R имеет вид
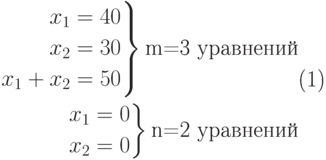 |
( 4.4) |
Т.к. C23+2=10, исследование десяти комбинаций (подсистем уравнений) по два уравнения из (9.4) выглядит следующим образом.
-
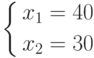 .
.Подставляем это уже готовое решение в третье ограничение задачи, x1+ x2 <= 50, и отвергаем его, т.к. ограничение не выполняется.
-
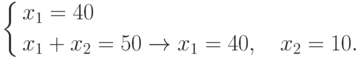 .
.Решение удовлетворяет третьему ограничению x2 <= 30.
Находим и запоминаем z(40, 10) = 130.
-
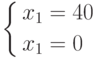 .
.Система не имеет решения.
-
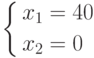 .
.Решение удовлетворяет ограничениям
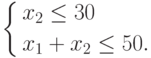 .
.Находим z(40, 0) = 80. Если мы решаем задачу не на параллельном компьютере, то сразу же видим, что новое значение z не превосходит уже найденное. Поэтому и это решение отвергаем.
-
 .
.Решение x1 = 20, x2 = 30 удовлетворяет и третьему "основному" ограничению задачи x1 <= 40. Находим z(20, 30) = 190. Запоминаем его вместе с решением, т.к. оно превосходит ранее полученное.
-
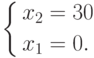 .
.Решение удовлетворяет всем ограничениям задачи. z(0, 30) = 150, что не превосходит уже найденное значение. Решение отвергаем.
-
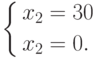 .
.Не имеет решения.
-
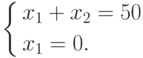 .
.Решение x1 = 0, x2 = 50 противоречит "основному" ограничению x2 <= 30. Отвергаем его.
-
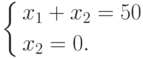 .
.Решение x1 = 50, x2 = 0 противоречит "основному" ограничению x1 <= 40. Отвергаем его.
-
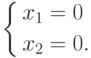 .
.Решение не противоречит "основным" ограничениям задачи. Однако z(0, 0) = 0, что не превосходит уже найденное значение. (Кстати, оно обеспечивает решение задачи z -> min.)
Итак, x1 = 20, x2 =30 обеспечивает zmax =190, т.е. является решением задачи ЛП.
Сложность алгоритма прямого перебора
Основным элементом решаемой задачи является решение системы n линейных уравнений. Сложность решения такой системы можно считать полиномиальной O(n3). Число решений определяется как Cnm+n. Чтобы найти зависимость сложности от основных параметров n и m, определим, во сколько раз увеличивается сложность при увеличении размерности n на единицу:
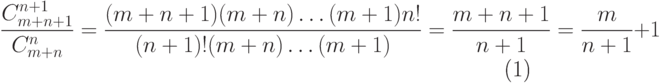 |
( 4.5) |
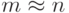 , то увеличение
размерности n на единицу при больших n примерно в
два раза
увеличивает сложность задачи, т.е. ее сложность определяется как O(2nn3). Это экспоненциальная сложность, практически сильно
ограничивающая размерность решаемых задач.
, то увеличение
размерности n на единицу при больших n примерно в
два раза
увеличивает сложность задачи, т.е. ее сложность определяется как O(2nn3). Это экспоненциальная сложность, практически сильно
ограничивающая размерность решаемых задач.Простота параллельного алгоритма прямого перебора делает его привлекательным для значений n порядка двух-трех десятков. Для большей размерности необходимо искать алгоритмы полиномиальной сложности.
