Структуры управления

Корректность

Оператор цикла в результате своего выполнения сохраняет свойство, заданное инвариантом, начиная с удовлетворения свойства, сохраняя свойство после каждой итерации, завершая работу с выполняемым свойством. Это сохранение свойства объясняет полученное им имя "инвариант", применимое здесь к инвариантам цикла (как к ранее инвариантам класса, которые подобным образом должны стать истинными в результате выполнения процедуры создания и оставаться истинными после каждого выполнения метода класса).

Как мы уже видели, цель цикла — в достижении определенного результата путем последовательных аппроксимаций. Шагами, направленными на достижение цели, являются инициализация и последовательное выполнение тела цикла. После каждого из этих шагов свойство устанавливает, что аппроксимация приближает финальный желаемый результат. Инвариант определяет аппроксимацию. В наших двух примерах инвариантами являются:

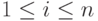• , как i-я аппроксимация, для , финального свойства
• "красная точка отображается в порядке следования станций, посещенных на линии до текущего момента", как аппроксимация заключительного свойства, что точка отображается на всех станциях линии.

Пусть Loop_invariant будет инвариантом. Когда выполнение цикла завершится, инвариант все еще будет выполняться по свойствам I1 и I2 принципа инварианта цикла. Кроме того, условие выхода из цикла Loop_exit также существует, так как в противном случае цикл никогда бы не завершился. Поэтому заключительным условием, истинным в момент завершения, является конъюнкция:

Loop_invariant and Loop_exit

Это условие и определяет результат выполнения цикла.

Корректность

Синтаксис подчеркивает эту связь — принцип постусловия цикла, — размещая предложения invariant и until друг за другом. Так что, если вы видите инвариант цикла и хотите знать, каков достигнут результат, просто посмотрите на два рядом идущих условия:

Рис. 7.7.

В примере с линией метро неформально условие выхода говорит: "все станции посещены". Конъюнкция этого условия с инвариантом говорит нам, что красная точка отображалась на всех станциях.

Принцип постусловия цикла является прямым следствием определения цикла как механизма аппроксимации. Цитируя предыдущее обсуждение, напомним, что идея состояла в выборе инварианта как некоторого обобщения цели:

• "достаточно слабого, чтобы его можно было применить к некоторому начальному подмножеству всего множества": в этом роль инициализации;
• "достаточно гибкого, чтобы позволять расширять множество, сохраняя его истинность": в этом роль тела цикла, выполняемого при истинности инварианта и ложности условия выхода из цикла. Тело цикла должно обеспечить расширение множества и сохранение инварианта;
• "достаточно сильного, чтобы из него следовала цель Post, когда он выполняется на всем множестве": это достигается на выходе, когда в соответствии с принципом постусловия цикла становится истинной конъюнкция условия выхода и инварианта.

Завершение цикла и проблема остановки

Согласно описанной схеме выполнения цикла тело цикла выполняется до тех пор, пока не будет выполнено условие выхода. Если цикл строится в соответствии с рассмотренной стратегией аппроксимации, то его выполнение завершится, так как рассматривается конечное множество данных, на каждом шаге происходит расширение подмножества хотя бы на один элемент, потому за конечное число шагов процесс обязательно завершится. Но синтаксис цикла допускает произвольную инициализацию, произвольное тело цикла и условие выхода, так что цикл может никогда не завершиться, как в этом примере:

from
  — "Любой оператор (возможно, пусто)" 
until
  0 /= 0
loop
  — "Любой оператор (возможно, пусто)"
end

В этом искусственном, но допустимом примере, условие цикла — которое, конечно, можно просто записать как False, — никогда не выполнится, так что цикл не может завершиться. Если запустить эту программу на компьютере, можно долго сидеть у экрана, где ничего не происходит, хотя компьютер работает. Осознав, что происходит что-то неладное, вы придете к решению, что нужно прервать выполнение (в EiffelStudio для этого есть специальная кнопка). Но у вас нет способа узнать — если вы пользователь программы и не имеете доступа к ее тексту, — "зациклилась" ли программа или просто идут долгие вычисления.

Если программа не завершается, то, хочу напомнить, это еще не является свидетельством ошибочного поведения. Некоторые программы проектируются специально так, чтобы они всегда работали, пока не будут явно остановлены. Прекрасным примером является операционная система (ОС), установленная на компьютере. Я был бы весьма разочарован, если бы при наборе этого текста произошло завершение работы ОС, которое бы означало, что система "рухнула" или я случайно нажал ногой кнопку выключения компьютера. Такая же ситуация существует с большинством "встроенных систем" (программ, выполняемых на различных устройствах): вы не захотите завершения программы мобильного телефона во время вашего разговора.

Но с другой стороны, обычные программы — в частности, большинство программ, обсуждаемых в этой книге, — устроены так, что, получив некоторый ввод, они вырабатывают результат за конечное число шагов.

Когда пишутся такие программы, можно непреднамеренно построить цикл, условие выхода из которого не будет выполняться, что приведет к тому, что вся программа не завершится. Чтобы избежать этого неприятного результата, лучший способ, позволяющий убедиться, что цикл завершится, состоит во введении для каждого цикла элемента, называемого вариантом цикла.

Определение: Вариант цикл

Если удается построить вариант, то тем самым доказывается завершаемость цикла за конечное число итераций, поскольку невозможно для неотрицательного целого значения уменьшаться бесконечно, оставаясь неотрицательным. Если мы знаем, что после инициализации вариант получил значение V, то после максимум V итераций цикл завершится, так как каждая итерация уменьшает вариант минимум на 1.

В этом доказательстве существенно, что вариант имеет целочисленный тип. Вещественный тип не годится, поскольку можно построить бесконечную уменьшающуюся последовательность, такую как 1, 1/2, 1/3, …, 1/n, … (это строго верно в математике; на компьютере, где бесконечности нет, множество закончилось бы, достигнув "машинного" нуля).

Если вы знаете вариант цикла, синтаксис позволяет вам указать его в предложении variant, следующем после тела цикла. Например, мы можем добавить спецификацию варианта цикла в наше вычисление максимума: from

Вариантом является выражение n — i. Он удовлетворяет требуемым условиям.

V1 Инициализация устанавливает i в 1. Предусловие цикла предполагает n ≥ 1. Так что вариант после инициализации неотрицателен.

V2 Тело цикла увеличивает i на единицу, соответственно уменьшая вариант.

V3 Если условие выхода не выполняется, то i будет меньше n (i < n, а не i <= n) и, следовательно, n — i, будучи уменьшенным на единицу, останется неотрицательным.

Из условия V3 следует, что недостаточно рассматривать отрицание условия выхода, которое говорит нам только, что i /= n: нам нужно быть уверенным, что i < n. Заметьте, для этого добавлены новые свойства в инвариант цикла: 1 <= i и i <= n. Они выполняются после инициализации цикла и сохраняются при выполнении очередной итерации. Поэтому, когда условие выхода не выполняется, i /= n, то с учетом инварианта i <= n фактически i < n.

Возможно, вы полагаете, глядя на этот пример, что много шума из ничего: и так понятно, что программа корректна и всегда завершится. Но на практике довольно часто встречаются программы, которые "зависают" по непонятным для пользователя причинам, и это означает, что в программе есть циклы, которые не завершаются. Возможно, что такая ошибка не обнаруживается на тестах, созданных разработчиком программы, поскольку тесты охватывают лишь малую часть возможных случаев и не всегда учитывают фантазию пользователя. Только благодаря выводу, проиллюстрированному выше, можно гарантировать — в вашей собственной программе — что цикл всегда завершится, вне зависимости от ввода.

Рассмотрение возможности незавершаемости программ приводит к введению важных понятий, изучаемых в отдельном курсе по теории вычислений.

Почувствуй теорию

Мы будем иметь возможность доказать утверждение о неразрешимости Проблемы Остановки сразу же после изучения подпрограмм в следующей лекции.

Почувствуй историю:

Неразрешимость Проблемы Остановки относится к серии отрицательных результатов, потрясавших одну область науки за другой, разрушая великие научные торжества, которые новое столетие поторопилось провозгласить.

• Математики, видя правильность теории множеств и основываясь на базисных методах логического вывода, смогли справиться с появлением видимых парадоксов, а затем, благодаря 30-летним усилиям Бертрана Рассела и Давида Гильберта по восстановлению основ математики, казалось, могли рассчитывать на успех. Но Курт Гёдель доказал, что в любой аксиоматической системе, достаточно мощной, чтобы описать обычную математику, всегда найдутся утверждения, которые нельзя ни доказать, ни опровергнуть. Теорема о неполноте является одним из наиболее поразительных примеров ограничений наших способностей к выводу.
• Примерно в то же время физикам пришлось принять принцип неопределенности Гейзенберга и другие результаты квантовой теории, ограничивающие наши способности наблюдения.

Результаты о неразрешимости, в частности, проблема остановки, являются компьютерными версиями таких, по-видимому, абсолютных ограничений.

Теоретическая неразрешимость Проблемы Остановки не должна оказать прямого воздействия на вашу практику программирования — за исключением эмоциональной травмы от осознания наших интеллектуальных ограничений, но я верю, что вы сумеете справиться с этим. Однако же программы, которые не завершаются, не просто теоретическая возможность — это реальная опасность. Чтобы избежать их неприятного появления, помните:

Почувствуй методологию

Анимация линии метро

В качестве простого примера цикла вернемся к задаче, в общих чертах рассмотренной в начале этой лекции, — анимации Линии 8 метро, устанавливая красную точку при посещении очередной станции. Мы можем использовать:

• из класса STATION запрос location, определяющий положение станции на карте. Результат запроса принадлежит типу POINT, представляющего точку в двумерном пространстве;
• команду show_spot из класса TOURISM, имеющую аргумент show_spot (p), где p типа POINT. Команда отображает красную точку в положении p;
• команду spot_time также из класса TOURISM, с предопределенным значением времени, в течение которого красная точка остается на каждой станции; сейчас оно имеет значение 0,5 секунды.

Задача цикла состоит в том, чтобы последовательно вызывать метод show_spot, передавая методу расположение каждой станции на линии.

Для последовательного получения станций мы можем (с помощью операций над переменными, изучаемыми в 9-й лекции) использовать запрос i_th, который дает нам i-й элемент линии при вызове some_line.i_th (i) для любого применимого i. Цикл должен выполнять

show_spot (Line8.i_th (i ).location)

для последовательных значений i, в пределах от 1 до LineS.count. Позвольте вместо использования этой возможности познакомить вас с типичной формой цикла, которая выполняет итерации над специальной структурой объектов, называемой списком. "Итерирование" структуры означает выполнение операции над каждым ее элементом или на некотором подмножестве элементов, заданном явным критерием. В данном примере операция состоит в вызове метода show_spot в точке расположения каждой выбранной станции.

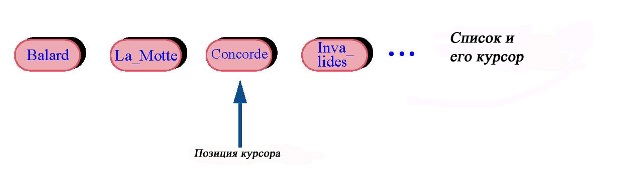
Классы, такие как LINE, вообще классы, описывающие упорядоченные списки объектов, поддерживают итерацию, позволяя передвигать курсор (специальную метку) к следующим элементам списка. Курсор не должен быть фактическим объектом, это абстрактное понятие, обозначающее в каждый конкретный момент позицию в списке.

Рис. 7.8. Список и его курсор

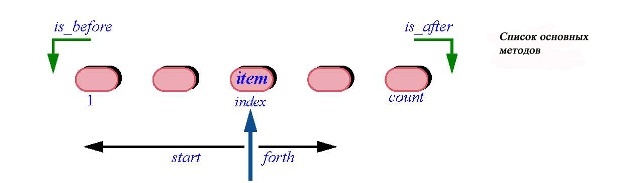
В показанном на рисунке состоянии курсор на третьей станции. Класс и другие классы, задающие списки, включают четыре ключевых метода — две команды и два запроса — для итерирования соответствующей структуры объектов:

• команду start, которая устанавливает курсор на первом элементе списка (в нашем примере элементом является станция метро);
• команду forth, которая передвигает курсор к следующему элементу;
• запрос item, возвращающий элемент списка, если он существует в позиции курсора;
• булевский запрос is_after, возвращающий True, если и только если курсор находится в позиции справа от последнего элемента (после списка). Для симметрии есть запрос is_before, хотя он нам пока не понадобится.

Рис. 7.9. Список основных методов

Полезен также запрос index, который, как показано, дает индекс текущей позиции курсора. Предполагается, что индекс позиции первого элемента равен 1 и равен count для последнего элемента.

Этого достаточно для построения общей схемы итерирования списка и ее применения в нашем случае:

from
Line8 .start 
invariant
— "Точка отображена для всех станций перед позицией курсора"
— "Другие утверждения, задающие инвариант (смотри ниже)" 
until
  Line8 .is_after
loop
  show_spot (Line8 .item .location) 
  Line8 .forth
variant
  Line8 .count - Line8 .index + 1
end

Эта схема, использующая start, forth, item и is_after для итерирования списка, столь часто встречается, что следует понимать все ее детали и быть в полной уверенности ее корректности. Неформально ее эффект ясен.

• Установить курсор на первый элемент списка, если он есть, вызвав start в разделе инициализации.
• На каждом шаге цикла в течение Spot_time секунд отображать точку на станции Line8.item в позиции курсора.
• После отображения точки на каждом шаге цикла передвинуть курсор на одну позицию, используя forth.
• Закончить цикл, когда курсор в позиции is_after, после последнего элемента.

Во избежание любых недоразумений (а я надеюсь, что предыдущее обсуждение не оставило им места) напомним - нет никакой связи между позицией станции на карте, ее местоположением и понятием позиции курсора:

• станция имеет географическое положение в городе, определяемое ее координатами;
• курсор существует только в нашем воображении и в нашей программе, но не во внешнем мире. Это внутренняя метка, позволяющая программе выполнять итерирование списка, запоминая от одного итерационного шага до другого, какой элемент был посещен последним.