Структуры управления

7.5. Циклы

Наша вторая структура управления — цикл — отражает одно из самых замечательных свойств компьютеров: их способность повторять операцию или варианты этой операции много раз, по человеческим меркам — очень много раз.

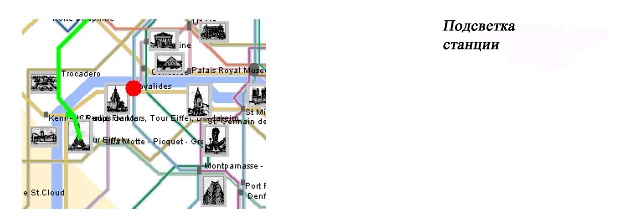
Типичным примером цикла является схема анимации, подсвечивающая линию метро и отображающая красную точку на каждой станции поочередно через каждые полсекунды. Система Show_line в поставке Traffic реализует этот сценарий. Вы можете выполнить ее, если желаете. Эффект выполнения одного из промежуточных шагов показан на рисунке:

увеличить изображение
Рис. 7.4. Подсветка станции

Этот эффект достигается благодаря циклу. Он использует show_spot (p) для отображения красной точки в точке p на экране через каждые полсекунды (значение, предопределенное для Spot_time). Для понимания деталей нам необходимы концепции, которые предстоит еще ввести по ходу обсуждения, так что пока просто посмотрите, как выглядит цикл.

Рис. 7.5. Тело цикла

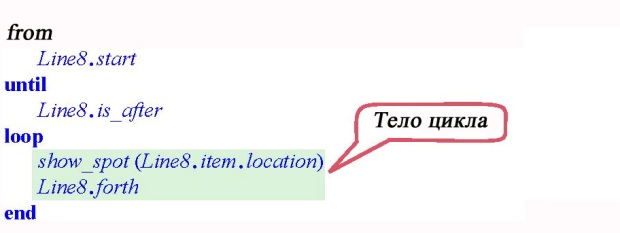
Цикл передвигает курсор (виртуальный маркер) к началу линии (start); затем, пока курсор не достиг последней позиции (is_after), он выполняет для каждой станции (item) следующие действия: отображает красное пятно в точке расположения станции — location, и передвигает курсор командой forth к следующей станции.

Каждое такое выполнение тела цикла называется итерацией цикла.

Рассмотрим ключевые составляющие цикла: инициализация (from), условие выхода (until) и повторно выполняемые действия (loop). Для получения полного понимания работы цикла следует предварительно проанализировать лежащие в его основе концепции.

Время программирования!

Цикл как аппроксимация

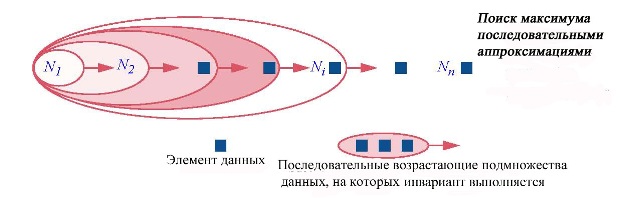
Как прием решения задач цикл является методом аппроксимации результата на последовательных, все расширяющихся подмножествах пространства задачи.

В примере с анимацией линии метро вся задача состоит в том, чтобы отобразить красную точку последовательно на каждой станции линии. Последовательными аппроксимациями являются: вначале точка не отображается ни на одной станции, затем отображается на первой станции, затем на второй, и так далее.

Вот еще один пример. Предположим, требуется узнать максимум множества из одного или нескольких значений . Следующая стратегия неформально описывает эту работу.

1. Положить max равным 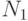. После этого справедливо, что max является максимумом множества, состоящего ровно из одного значения, .
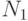2. Затем для каждого последовательного i = 2, 3,..., n выполнять следующее: если 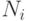больше чем текущее значении max, переопределить max, сделав его равным .

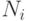Из этого следует, что на i-м шаге (где первый шаг соответствует случаю I1, а последующие шаги — случаю I2 для i = 2, i = 3 и т.д.) действует следующее свойство, называемое инвариантом цикла.

Инвариант цикла стратегии "максимум" на шаге i

max является максимумом из :

Этот инвариант для n-го шага, случай I2 для i = n, дает

что и является желаемым результатом.

Следующая картинка иллюстрирует стратегию цикла для этого случая.

Рис. 7.6. Поиск максимума последовательными аппроксимациями

Цикл вначале устанавливает инвариант "max является максимумом первых i значений" для тривиального случая: i = 1. Затем повторно расширяется множество данных, на котором выполняется инвариант.

В примере с анимацией линии метро инвариантом является утверждение "красная точка отображалась на всех уже посещенных станциях".

Понятие инварианта не стало новым, так как мы уже знакомы с инвариантами класса. Две формы инварианта являются связанными, так как обе описывают свойство, которое некоторые операции должны сохранять. Но роли их различны: инвариант класса применим ко всему классу и должен сопровождать выполнение методов класса. Инвариант цикла применим к одному определенному циклу и должен сопровождать каждую итерацию цикла.

Стратегия цикла

Хотя большинство циклов более сложные, чем простой пример вычисления максимума, он иллюстрирует общую форму цикла как стратегию решения задач.

Эта стратегия полезна, когда задача сводится к следующей постановке. Мы начинаем с некоторого начального свойства Pre, и нам требуется достичь выполнения некоторой цели Post, характеризующей множество данных DS. Это множество конечно, хотя и может быть очень большим.

Чтобы использовать цикл, нужно найти слабую (более общую) форму цели Post: свойство INV (s) — инвариант цикла, определенный на подмножествах s из DS со следующими свойствами.

L1. Можно найти начальное подмножество Init из DS, такое, что начальное условие Pre влечет INV (Init ); другими словами, инвариант выполняется на начальном подмножестве.

L2. INV (DS) влечет Post (из истинности инварианта на всем множестве следует истинность цели).

L3. Известен способ, позволяющий расширить подмножество s, для которого инвариант INV(s) выполняется, на большее подмножество (s’) из DS, сохраняя при этом истинность инварианта.

Пример с максимумом имеет все три составляющие: DS — это множество чисел ; предусловие Pre говорит, что DS имеет, по меньшей мере, один элемент; цель Post утверждает, что найден максимум этих чисел, а инвариант INV(s), где s — подмножество 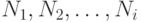, утверждает, что найден максимум на этом подмножестве. Тогда:

M1. Если Pre выполняется, (имеется хотя бы одно число), то нам известно начальное множество Init, такое, что INV (Init) выполняется. Для этого достаточно в качестве подмножества взять первый элемент .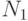

M2. INV (DS) — инвариант, применимый ко всему подмножеству — влечет истинность цели, а фактически совпадает с целью Post.

M3. Когда INV(s) удовлетворяется на 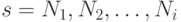, которое пока не совпадает со всем DS — другими словами, i < n, — то мы можем установить INV (s') для большего подмножестваs’ из DS: мы просто возьмем s' как 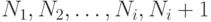, а в качестве нового максимума большее из двух чисел: старого максимума и 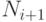. Заметьте: в общем случае нужно крайне тщательно проектировать инвариант, чтобы он позволял применить стратегию последовательной аппроксимации.

• INV должен быть достаточно слабым, чтобы его можно было применить к некоторому начальному подмножеству, обычно содержащему совсем немного элементов из всего множества.
• Он достаточно силен, чтобы из него следовала цель Post, когда он выполняется на всем множестве.
• Он достаточно гибкий, чтобы позволять расширять множество, сохраняя его истинность.

Начав с начального подмножества и повторяя расширения, мы придем к желаемому результату. Эта стратегия последовательной аппроксимации цели на прогрессивно растущих подмножествах может требовать большого числа итераций, но компьютеры быстры, и они не бастуют, требуя покончить с однообразной работой.

Эти наблюдения определяют, как работает цикл в качестве структуры управления. Его выполнение проходит следующие этапы.

X1. Устанавливается INV (Init), используя преимуществ L1. Это дает нам Init как первое подмножество s, на котором выполняется INV.

X2. До тех пор, пока s не совпадает со всем множеством DS, применяется прием L3 для установления INV на новом, расширенном s.

X3. Останавливаемся сразу же, когда s совпадает с DS. В этот момент INVвыполняется на DS, что, благодаря L2, свидетельствует о достижении цели Post.

Этот процесс гарантирует завершаемость, поскольку мы предполагаем, что DS является конечным множеством, s всегда остается подмножеством DS и на каждом шаге увеличивается по крайней мере на один элемент, так что гарантируется, что после конечного числа шагов s совпадет с DS. В некоторых случаях, однако, установление завершаемости не столь просто.

Оператор цикла: базисный синтаксис

Для выражения стратегии цикла в тексте программы будем использовать для нашего примера "максимума" следующую общую структуру:

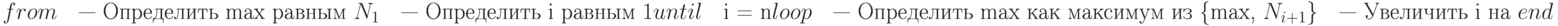
На данный момент все составляющие операторы являются псевдокодом. Пример демонстрирует три требуемые части конструкции цикла (дополненные позже двумя возможными частями).

• Предложение from вводит операторы инициализации (X1).
• Предложение loop вводит операторы, выполняемые на каждой последовательной итерации (X2).
• Предложение until вводит условие выхода — условие, при котором итерации завершаются (X3).

Эффект выполнения этой конструкции, задаваемой ключевыми словами(from, until, loop), определяется в соответствии с предыдущим обсуждением.

• Первым делом выполняются операторы предложения from (инициализация).
• Пока не выполняется условие выхода в предложении until, выполняются операторы предложения loop (тело цикла).

Более точно это означает, что после инициализации тело цикла может быть выполнено:

• ни разу, если условие выхода из цикла выполняется сразу же после инициализации;
• один раз, если выполнение тела цикла приводит к выполнению условия выхода;
• общая ситуация: i раз для некоторого i, если условие выхода будет ложным для всех j выполнений тела цикла 1 ≤ j < i и становится истинным после i-го выполнения.

Синтаксически предложения from и loop каждое содержат составной оператор. Как следствие, здесь можно использовать произвольное число операторов, в том числе и ноль. Это происходит, например, если цикл не нуждается в явной инициализации (в тех случаях, когда контекст, предшествующий циклу, обеспечивает истинность инварианта цикла); тогда предложение from будет пусто.

From
         <------- Здесь ничего
until
  — "Условие выхода"
loop
  — "Тело цикла"
end

В теле цикла должно быть некое продвижение в процессе аппроксимации (добавить хотя бы один новый элемент к подмножеству предыдущего обсуждения); в противном случае процесс никогда не завершится. Поэтому в реальных программах никогда не встречается цикл с пустым предложением loop.

Включение инварианта

Базисная форма цикла, как мы видели, не показывает инвариант цикла. А жаль, так как инвариант является основой для понимания того, что цикл делает. Поэтому рекомендуемая и возможная форма записи цикла включает предложение invariant. С данным предложением цикл выглядит так:

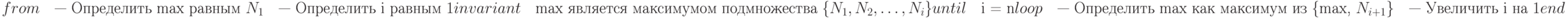
Инвариант в этом примере — все еще псевдокод, но тем не менее, он полезен, так как поставляет важную информацию о цикле.

Оператор цикла: корректность

Инвариант цикла имеет два важных характеристических свойства.