Решение уравнений

4.4. Задачи оптимизации

В программе MathCAD с успехом решаются задачи оптимизации. Задача оптимизации (линейного программирования) - определение значений аргументов функции, при которых функция имеет экстремальное (минимальное, максимальное) значение. Условия, налагаемые на аргументы функции - заданные ограничения. Используется методика решения системы уравнений помощью блока Given. При этом вместо функции Find используется функция Maximize(), если определяется максимум, и функция Minimize() , если определяется минимум оптимизируемой функции. Последовательность действий следующая:

• ввести оптимизируемую функцию,
• определить начальные значения аргументов,
• в блоке Given ввести уравнения (неравенства) ограничений,
• ввести функцию Maximize () (Minimaze() ),
• определить решение.

Задача решается в алгебраическом и матричном виде. В матричном виде начальное значение корней, ограничения задаются в виде матриц. Решение в обоих случаях получается в виде матрицы.

Пример 4.11

Найти максимум функции

при ограничениях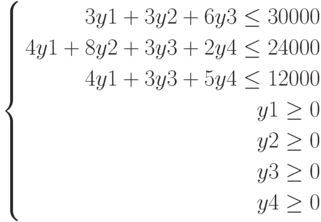

Листинги решения в алгебраическом и матричном виде.

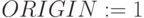
Оптимизируемая функция – поиск максимума,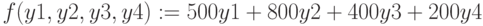

Начальные значения:

, , ,

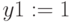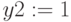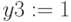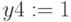
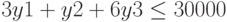
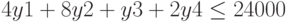
Ограничения:

, , ,

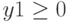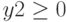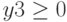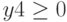
Решение:

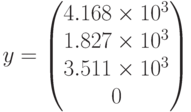
Максимальное значение функции: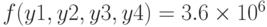

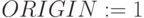
Матрица коэффициентов функции: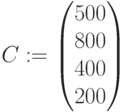

Матрица левых частей ограничений: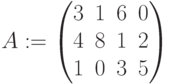

Матрица правых частей ограничений: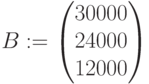

Начальные значения:

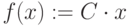
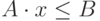
Решение:

Максимальное значение функции:

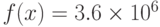
Основные итоги

В лекции представлены методы численного решения уравнений и систем уравнений с использованием функций MathCAD. Рассмотрены функция Root (), функция для поиска корней полинома polyroots(), вычислительные блоки Given .Find() и Given Minerr().. Описано численное решение систем линейных уравнений, а также способы аналитического решения : с помощью матриц, функции lsolve(), символьного оператора solve. Показано решение задач оптимизации.

Задания для самостоятельного выполнения

1. Построить графики функций. Решить уравнения с применением функции root()

   а) 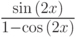для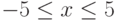

   б)

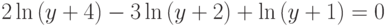
   в) 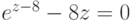(2 корня)
2. Решить с применением функции polyroots() следующие уравнения

   а)

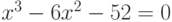
   б)
3. Решить системы уравнений с использованием блока Given Find(.)

   а) 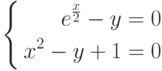найти 3 корня

   б) 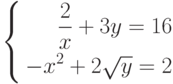найти 2 корня

   в)

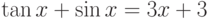
   г)

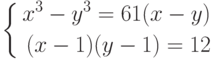
   д)
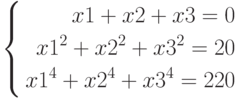
4. Решить систему уравнений тремя способами.

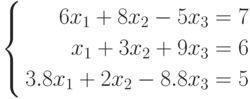
Ключевые термины

root() – функция для численного решения нелинейного уравнения с одним неизвестным. Возвращает с заданной точностью значение переменной, при котором функция равна нулю.

polyroot() - функция для численного поиска корней полинома. Возвращает вектор длиной n+1 всех корней полинома степени n.

Given Find() – вычислительный блок для численного решения нелинейных уравнений и систем уравнений.

Given Minerr() вычислительный блок для приближенного численного решения нелинейных уравнений и систем уравнений.

Maximize () – функция для поиска значений переменных функции, при которых функция имеет максимальное значение.

Minimaze() - , функция для поиска значений переменных функции, при которых функция имеет минимальное значение.

lsolve(A,B) - функция аналитического решения системы линейных уравнений, представленной в виде AX=B.