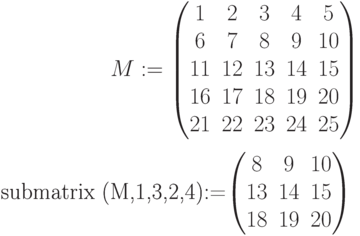Встроенные функции MathCAD

Часто используемые функции

augment(A,B) - Возвращает матрицу, сформированную путем размещения массива В справа от массива А. А и В должны иметь одинаковое число строк:

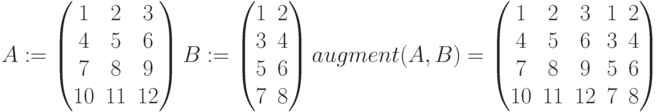
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:

cols(A) – число столбцов матрицы А.

csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:

eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:

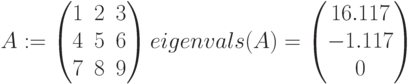
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.

floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:

identity(n) – создает единичную матрицу размером

length(v) – длина вектора v.

max(v) – максимальный по значению элемент вектора v.

min(v) – минимальный по значению элемент вектора v.

maximize(f,v) – возвращает вектор размерности n, который обеспечивает функции f максимальное значение. Функция f – функция n переменных; вектор v – вектор начальных приближений ответа;

minimize(f,v) - возвращает вектор размерности n, который обеспечивает функции f минимальное значение. Обращение аналогично функции Maximize.

mean(M) – среднее арифметическое элементов вектора или матрицы.

median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:

rbeta (m, s ₁, s₂)Возвращает вектор m случайных чисел, имеющих бэта-распределение. 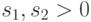есть параметры формы.

rbinom (m, n, p) Возвращает вектор m случайных чисел, имеющих биномиальное распределение. . n есть натуральное число.

rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, есть параметр формы.

rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. .

rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а есть параметр масштаба.

rnorm (m,l, s) Возвращает вектор m случайных чисел, имеющих нормальное распределение. .

rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. .

rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента..

runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. .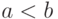

rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).

round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n<0, то y округляется до n знаков слева от десятичной точки.

rows(A) – число строк матрицы А.

rsort(B,n) – сортирует столбцы матрицы В таким образом, чтобы расположить элементы строки n в порядке возрастания:

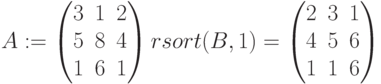
Нумерация строк по умолчанию начинается с нуля.

submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc: