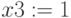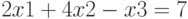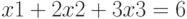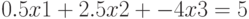Решение уравнений

4.3. Системы линейных уравнений

Рассмотрим задачу решения системы из n линейных уравнений. Пусть нам дана система уравнений:

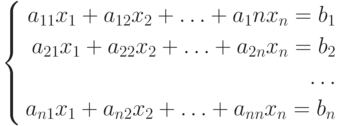
Решить систему – значит найти такие числа, при подстановке которых в данную систему получим все n верных равенств. Составим матрицы системы.

• Составляем матрицу A, состоящую из коэффициентов при переменных (размерность n x n).
• Составляем матрицу свободных членов B (размерность ( n x 1).
• Перепишем и исходную систему в матричном виде: .

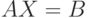Матричный способ

Система решается аналитически. Вектор решения можно получить из следующего выражения: 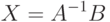. Можно сделать проверку подстановкой корней в уравнения.

Пример 4.6

Решить систему уравнений матричным способом. Сделать проверку.

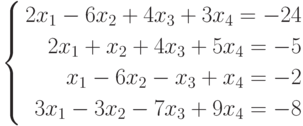
Ниже представлено решение через обратную матрицу. Найден определитель, чтобы убедиться в существовании решения.

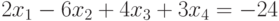
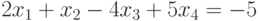
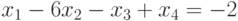
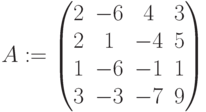
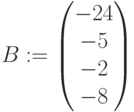
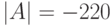
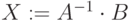
Проверка: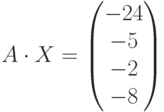

Использование функции lsolve()

В системе MathCAD введена встроенная функция lsolve (A,B), которая решает систему аналитически и возвращает вектор X для системы линейных уравнений 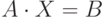при заданной матрице коэффициентов А и векторе свободных членов В.

Пример 4.7

Решить систему примера 4.6, используя функцию lsolve()

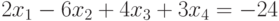
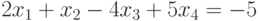
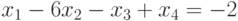
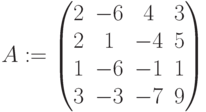
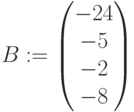
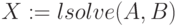
Символьное решение

Для решения применяем символьные преобразования. Преимуществом символьного решения является возможность решения уравнений в общем виде. Используем оператор Solve.

Пример 4.8

Пусть функции r (x,y) w(x,y) заданы системой уравнений. Найти r и w , решив систему.

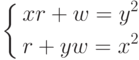
Записываем систему в виде матрицы, используя логическое равенство, решается система относительно r (x,y) w(x,y) ,они тоже записываются в виде матрицы.

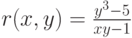
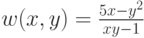
Пример 4.9

Решить аналитически систему уравнений:

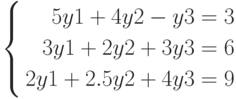
На листинге показано точное решение системы и решение с точностью до 3 значащих цифр. Операторы solve и float набираются последовательно .

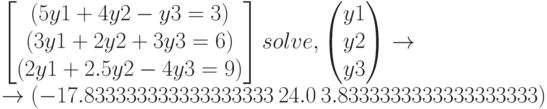
Иногда сложные уравнения символьно не решаются, поэтому приходится обращаться к численным методам.

Численное решение. Использование блока Given Find()

Решение в скалярной форме. В данном методе система уравнений вводится без использования матриц, в "натуральном" виде. Операция аналогична решению системы

Пример 4.10

Решить систему уравнений, используя блок Given Find():

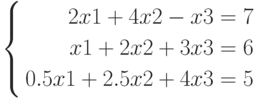
Предварительно указать начальные значения неизвестных. Это могут быть любые числа, входящие в область определения. (Часто за них принимают столбец свободных членов).

, ,
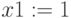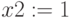