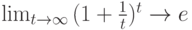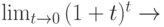НОУ ИНТУИТ | MATHCAD 14: Основные сервисы и технологии. Лекция 2: Символьные вычисления

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Уральский государственный экономический университет

Опубликован: 24.04.2013 | Доступ: свободный | Студентов: 2937 / 1132 | Длительность: 06:24:00

Темы: Математика, Программное обеспечение, Физика, Образование

Специальности: Математик, Физик

Теги: алгебра, анализ, вычисления, теория вероятностей, теория чисел

|

Вам нравится? Нравится 80 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2.2.Символьные операции с оператором символьного вывода

Мощное и удобное средство символьных операций - оператор символьного вывода. Используя этот оператор, можно дифференцировать, интегрировать в символьном виде и производить другие операции. Этот способ более нагляден, так как позволяет записывать выражения в традиционной математической форме и сохранять символьные вычисления в документах MathCAD. Следует иметь в виду, что оператор символьного вывода учитывает все предыдущее содержимое документа и выдает результат с его учетом. Не всякое выражение поддается аналитическим преобразованиям. В случае, если задача не имеет аналитического решения, либо она оказывается слишком сложной для символьного процессора, то в качестве результата выводится само выражение.

Оператор и символьные операции можно вызвать из панели инструментов Symbolic (иконка палитры имеет вид ) или Evaluation (Рис.2.6 а,б).

Рис. 2.6. Палитра символьных операций а) Symbolic, б) Evaluation

Выполнение символьной операции

Ввести выражение. Обязательно выделить его с помощью синего уголка (клавиша "пробел"), синий уголок справа.
Щелкнуть оператор символьного вывода.
Щелкнуть за пределами.
Проделать операции.

Символьные операции с ключевыми словами

До определённой степени можно управлять способом символьных вычислений. Для всестороннего контроля над символьными преобразованиями нужно использовать ключевые слова (keywords) панели Symbolic. Ключевые слова символьных преобразований представлены в таблице 2.1

Выполнение символьной операции с ключевым словом:

Ввести выражение. Обязательно выделить его с помощью синего уголка.
Щелкнуть соответствующую операцию – ключевое слово на палитре Symbolic.
Если надо произвести две операции, щелкнуть другую операцию (ключевое слово).
Щелкнуть за пределами.

Команды панели Symbolic

Таблица 2.1.
Команда меню	Назначение
Float, n	Выполнить вычисление, результат представить форме числа с плавающей точкой с точностью до n значащих цифр.
rectangular	Выполнить вычисление с представлением результата в комплексной форме
assume	Выполнить вычисление с предположениями
simplify	Упростить выражение
expand	Разложить выражение по степеням
factor	Разложить на множители
collect	Группировка по степеням переменной
coeffc	Найти коэффициенты полинома
solve	Решить уравнение (систему уравнений) относительно переменной
substitute	Замена переменной
differentiate	Дифференцировать все выражение относительно выделенной переменной
Integrate	Интегрировать выражение относительно выделенной переменной
parFrac	Разложить на элементарные дроби
series	Разложить в ряд Тейлора
fourier	Преобразование Фурье
invfourier	Обратное преобразование Фурье
laplace	Преобразование Лапласа
invlaplace	Обратное преобразование Лапласа
ztranns	Z-преобразование
invztranns	Обратное Z-преобразование
combine	Упростить выражение для экспоненциальной или логарифмической функции

Дифференцирование и интегрирование

Для дифференцирования ввести функцию под знак 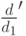$\frac{d}{d_1}'$ используя панель Calculus. Обязательно выделить его с помощью синего уголка (клавиша "пробел"), синий уголок справа.
Для интегрирования ввести функцию под знак 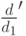$\frac{d}{d_1}'$ . Также выделить его с помощью синего уголка (клавиша "пробел"), синий уголок справа.
Щелкнуть оператор символьного вывода, используя панель Symbolic или Evaluation.
Щелкнуть за пределами.

Примеры символьного дифференцирования и интегрирования (вычисления тройного интеграла и определенного интеграла с параметрами а,b) показаны ниже. Аналогичным образом в символьном виде можно вычислить производные любого порядка, суммы, произведения.

Не все интегралы, тем более двойные и тройные, MathCAD может вычислить в символьном виде. Если MathCAD не может совершить операцию, он выводит первоначальное выражение.

$\frac{d}{dx}{[\frac{1}{\sin{(x)^2}(1-\cos{(x)})}]}\to\frac{-2}{\sin{(x)^3}(1-\cos{(x)})}\cdot \cos{(x)}-\frac{1}{\sin{(x)}(1-\cos{(x)})^2}$

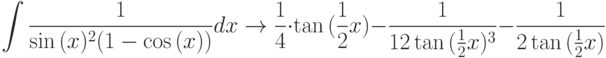
$\int{\frac{1}{\sin{(x)^2}(1-\cos{(x)})}}dx\to\frac{1}{4}\cdot \tan{(\frac{1}{2}x)}-\frac{1}{12\tan{(\frac{1}{2}x)^3}}-\frac{1}{2\tan{(\frac{1}{2}x)}}$

Вычисление пределов

Ввести функцию под знак $\lim_{t\to\ 0}$ используя панель Calculus. Обязательно выделить его с помощью синего уголка (клавиша "пробел"), синий уголок справа.
Щелкнуть оператор символьного вывода, используя панель Symbolic или Evaluation.
Щелкнуть за пределами.
Проделать операции, перечисленные ниже.

Замечательные пределы

$\lim_{t \to 0} \frac{\sin{(t)}}{t} \to 1$
$\lim_{t \to \infty} {(1+\frac{1}{t})^t} \to e$
$\lim_{t \to 0} {(1+t)^t} \to$

Преобразование выражений

Упрощение выражений. Для выполнения операции преобразования необходимо выбрать соответствующее ключевое слово Simplify (Упрощение), Factor (разложение на множители) или Expand (расширение выражений) на панели Символика. Пример команд Simplify, Expand, Factor приведен ниже.

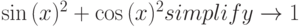
$\sin{(x)^2}+\cos{(x)^2} simplify \to 1$

$\frac{a^2-b^2}{(a+b)(a-b)} simplify \to 1$

$\frac{-5}{x}+\frac{5}{x-1}-\frac{5}{(x-1)^2}+\frac{6}{(x-1)^3}-\frac{4}{(x-1)^4} simplify \to \frac{(x^2-5)}{[x(x-1)^4]}$

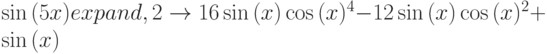
$\sin{(5x)} expand,2 \to 16\sin{(x)}\cos{(x)^4}-12\sin{(x)}\cos{(x)^2}+\sin{(x)}$

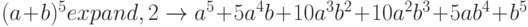
$(a+b)^5 expand,2 \to a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5$

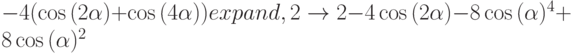
$-4(\cos{(2\alpha)}+\cos{(4\alpha)}) expand,2 \to 2-4\cos{(2\alpha)}-8\cos{(\alpha)^4}+8\cos{(\alpha)^2}$

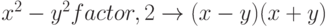
$x^2-y^2 factor,2 \to (x-y)(x+y)$

$[(a)^2-2ab+b^2] factor,2 \to (a-b)^2$

$\sum_n{x-n} factor,2 \to n(x-1)$

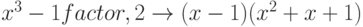
$x^3-1 factor,2 \to (x-1)(x^2+x+1)$

Разложение по степеням переменной. Команда Collect разлагает выражение по степеням указанной в этой команде переменной, если такое представление возможно. Пример использования команды Collect приведен ниже.

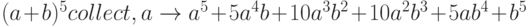
$(a+b)^5 collect,a \to a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5$

$(x-a)(x-b)(x-c) collect,x \to x^3+(-a-b-c)x^2+[ab-(-a-b)c]x-abc$

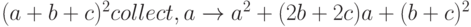
$(a+b+c)^2 collect,a \to a^2+(2b+2c)a+(b+c)^2$

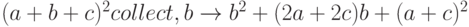
$(a+b+c)^2 collect,b \to b^2+(2a+2c)b+(a+c)^2$

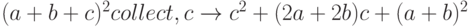
$(a+b+c)^2 collect,c \to c^2+(2a+2b)c+(a+b)^2$

Подстановка значений переменных в выражение и вычисление этого выражения. Используется слово Substitute. Пример использования команды Substitute приведен ниже.

$ax^2+bx+c subsctitute,x=5 \to 25a+5b+c$

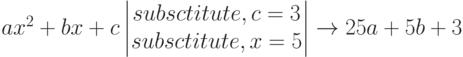
$ax^2+bx+c \begin{vmatrix} subsctitute,c=3 \\ subsctitute,x=5 \end{vmatrix} \to 25a+5b+3$

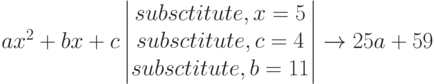
$ax^2+bx+c \begin{vmatrix} subsctitute,x=5 \\ subsctitute,c=4 \\ subsctitute,b=11 \end{vmatrix} \to 25a+59$

$ax^2+bx+c \begin{vmatrix} subsctitute,x=5 \\ subsctitute,c=3 \\ subsctitute,b=4 \\ subsctitute,a=3 \end{vmatrix} \to 98$

Решение уравнений

Ключевое слово Solve позволяет решать уравнения и системы линейных и нелинейных уравнений. При решении уравнений с нулевой правой частью надо ввести выражение, ключевое слово Solve, переменную, относительно которой решается уравнение. Пример решения приведен ниже.

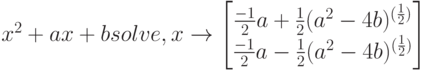
$x^2+ax+b solve,x \to \begin{bmatrix} \frac{-1}{2}a+\frac{1}{2}(a^2-4b)^{(\frac{1}{2})} \\ \frac{-1}{2}a-\frac{1}{2}(a^2-4b)^{(\frac{1}{2})} \end{bmatrix}$

$e^x-a solve,x \to \ln{(a)}$

Если уравнения имеют правую часть, используется логическое равенство с панели Boolean. Система уравнений и переменные, относительно которых система решается, вводятся как элементы матрицы (см. ниже).

$\left(\begin{array}{c} x+y=2\\ 2x-y=1 \end{array}\right) solve, \left(\begin{array}{c} x \\ y \end{array}\right) \to (1,1)$

При решении уравнений с определенной точностью вводится ключевое слово float (см. ниже).

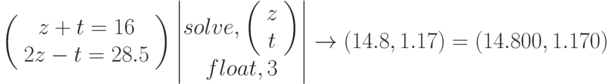
$\left(\begin{array}{c} z+t=16\\ 2z-t=28.5 \end{array}\right) \begin{vmatrix} solve, \left(\begin{array}{c} z \\ t \end{array}\right) \\ float,3 \end{vmatrix} \to (14.8, 1.17)=(14.800, 1.170)$

Основные итоги

В лекции представлены символьные вычисления в различных вариантах: с помощью команд меню, оператора символьного вывода, ключевых слов символьного процессора. На примерах показано дифференцирование и интегрирование математических выражений, вычисление пределов, решение уравнений, различные преобразования алгебраических выражений.

Задания для самостоятельного выполнения

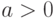
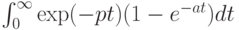
Найти интеграл для и $\int_0^\infty\exp(-pt)(1-e^{-at})dt$
Найти выражение, подставив и
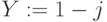
Решить уравнение
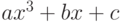
- в общем виде
- для
- численное решение до 4 знака
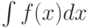
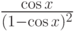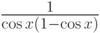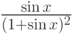Вычислить неопределенный интеграл $\int f(x)dx$ $\frac{\cos{x}}{(1-\cos{x})^2}$ , $\frac{\cos{x}}{(1+\cos{x}+\sin{x})^2}$ , $\frac{1}{\cos{x}(1-\cos{x})}$ , $\frac{\sin{x}}{(1+\sin{x})^2}$ .
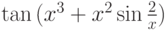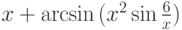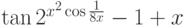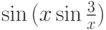Найти производную функции : $\tan{(x^3+x^2\sin{\frac{2}{x}})}$ , $x+\arcsin{(x^2\sin{\frac{6}{x}})}$ , $\arctan{x\cos{\frac{1}{5x}}}$ , $\tan{2^{x^2\cos{\frac{1}{8x}}}-1+x}$ , $\sin{(x\sin{\frac{3}{x}})}$ .
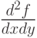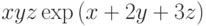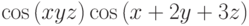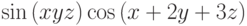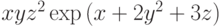Найти частные производные $\frac{d^2f}{dxdy}$ : $xyz\exp{(x+2y+3z)}$ , $\cos{(xyz)}\cos{(x+2y+3z)}$ , $\sin{(xyz)}\cos{(x+2y+3z)}$ , $\sqrt{x^2+2xyz+3z^3}$ , $(x^2-y^3+z)\sin{(x+2y+3z)}$ , $xyz^2\exp{(x+2y^2+3z)}$ .