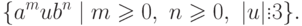|
Упражнение 2.1.25 |
Синтаксические моноиды
Основная цель данной лекции - доказать еще один критерий автоматности формального языка. Этот критерий можно сформулировать в терминах классов эквивалентности слов по взаимозаменяемости (однако формальные определения будут даны без использования понятия класса эквивалентности). Слова x и y считаются взаимозаменяемыми (относительно языка L ), если при замене в любом слове из языка L подслова, совпадающего с x, на y снова получится слово из языка L и наоборот. В разделе 6.3 фактически доказывается, что язык L является автоматным тогда и только тогда, когда соответствующее отношение взаимозаменяемости разбивает множество всех слов рассматриваемого алфавита на конечное число классов эквивалентности.
Но сначала мы докажем аналогичный результат для отношения взаимозаменяемости не подслов, а префиксов (раздел 6.1). Соответствующие классы эквивалентности слов позволяют построить минимальный детерминированный конечный автомат для заданного языка. Известен и другой метод нахождения минимального детерминированного конечного автомата (раздел 6.2), но этот метод можно применять только тогда, когда уже имеется какой-нибудь детерминированный конечный автомат, распознающий данный язык. В конце лекции доказывается, что классы эквивалентности по взаимозаменяемости относительно автоматного языка сами являются автоматными языками.
6.1. Множества правых контекстов
Определение 6.1.1.
Пусть  и
и  .
Тогда множество правых контекстов
слова y относительно языка L
определяется следующим образом:
.
Тогда множество правых контекстов
слова y относительно языка L
определяется следующим образом:

Пример 6.1.2.
Пусть 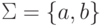 и
и  .
Тогда
.
Тогда
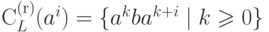
- если
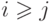 ,
то
,
то 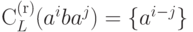 ;
; - если
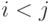 ,
то
,
то 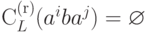 ;
; - если
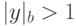 ,
то
,
то 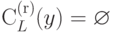 .
.
Определение 6.1.3.
Для любого состояния p
полного детерминированного конечного автомата  и любого слова w
обозначим через
и любого слова w
обозначим через  такое состояние q,
что существует путь из p в q с меткой w
(в силу полноты и детерминированности такое состояние
существует и единственно).
такое состояние q,
что существует путь из p в q с меткой w
(в силу полноты и детерминированности такое состояние
существует и единственно).
Лемма 6.1.4. Если язык L
распознается полным детерминированным конечным автоматом  ,
то
,
то

Доказательство. Пусть I = {s}. Введем обозначение
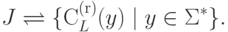
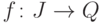 ,
положив f(A)
равным
,
положив f(A)
равным 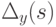 ,
где y -
некоторое слово,
для которого выполнено условие
,
где y -
некоторое слово,
для которого выполнено условие 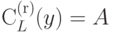 (если существует несколько таких слов y,
то можно использовать, например, первое среди них
в лексикографическом порядке).
(если существует несколько таких слов y,
то можно использовать, например, первое среди них
в лексикографическом порядке).Заметим, что
для любых слов u и v,
если  ,
то
,
то 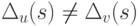 .
Следовательно, функция f
является инъективной.
Но тогда
.
Следовательно, функция f
является инъективной.
Но тогда 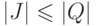 .
.
Пример 6.1.5.
Рассмотрим язык L,
порождаемый полным детерминированным конечным автоматом  из примера 2.6.4.
Тогда
из примера 2.6.4.
Тогда
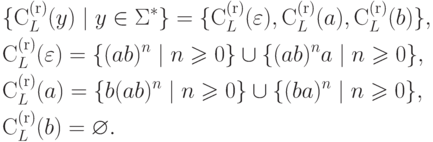
Лемма 6.1.6. Если  и множество
и множество 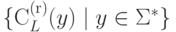 конечно, то язык L является автоматным.
конечно, то язык L является автоматным.
Доказательство.
Язык L
распознается полным детерминированным конечным автоматом  ,
где
,
где
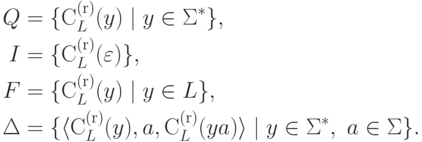
Пример 6.1.7.
Пусть 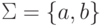 .
Рассмотрим автоматный язык L = a+b*.
Обозначим
.
Рассмотрим автоматный язык L = a+b*.
Обозначим

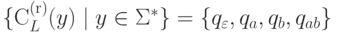 .
Язык L
распознается полным детерминированным конечным автоматом
.
Язык L
распознается полным детерминированным конечным автоматом  ,
где
,
где 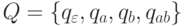 ,
, 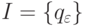 ,
, 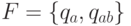 ,
,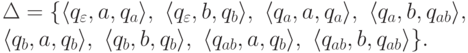
![\objectwidth={7.5mm} \objectheight={7.5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{q_\varepsilon}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" ^{a}
\ar "2,3" _{b}
& *=[o][F=]{q_a}
\rloop{0,1} ^{a}
\ar "1,3" ^{b}
& *=[o][F=]{q_{ab}}
\ar "2,3" ^{a}
\rloop{0,1} ^{b}
\\
%
&
& *=[o][F-]{q_b}
\rloop{1,0} ^{a}
\rloop{0,-1} ^{b}
}](/sites/default/files/tex_cache/27ef2e8e106fe21793369a485ba274ce.png)
Теорема 6.1.8. Язык  является автоматным
тогда и только тогда, когда
множество
является автоматным
тогда и только тогда, когда
множество 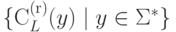 конечно.
конечно.
Доказательство. Необходимость доказана в лемме 6.1.4, достаточность - в лемме 6.1.6.
Замечание 6.1.9. В силу леммы 6.1.4 полный детерминированный конечный автомат, построенный в доказательстве леммы 6.1.6, является минимальным (по количеству состояний) среди всех полных детерминированных конечных автоматов, распознающих заданный язык. Можно доказать, что любой минимальный полный детерминированный конечный автомат, распознающий заданный язык, изоморфен этому автомату.
Упражнение 6.1.10. Пусть 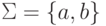 и
и

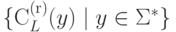 ?
?Упражнение 6.1.11. Найти минимальный полный детерминированный конечный автомат для языка {ab,abb}*.
Упражнение 6.1.12. Найти минимальный полный детерминированный конечный автомат для языка
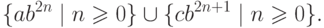
Упражнение 6.1.13. Найти минимальный полный детерминированный конечный автомат для языка
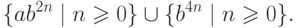
Упражнение 6.1.14. Найти минимальный полный детерминированный конечный автомат для языка