|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2.? |
Комбинаторные задачи с ограничениями
Задачи с ограничением на порядок
До сих пор мы рассматривали задачи, в которых на порядок элементов в комбинациях не накладывалось никаких ограничений или дополнительных условий. Либо (как в сочетаниях) порядок вообще не учитывался . Рассмотрим задачи с ограничением.
Задача 1. Укротитель хищных зверей хочет вывести на арену 5 львов и 4 тигра, при этом нельзя , чтобы два тигра шли друг за другом. Сколькими способами он может расположить зверей?
Обозначим львов буквой Л. Для тигров имеется 6 мест.
_____Л1_____Л2_____Л3____Л4_____Л5______
Львов можно расположить 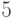 ! Способами, то есть 120. На шести местах для тигров их можно расположить
! Способами, то есть 120. На шести местах для тигров их можно расположить 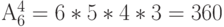 способами.
способами.
Общее число способов 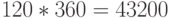 .
.
Для задачи в общем виде, если имеется:  тигров и
тигров и  львов.
львов.
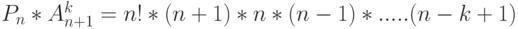 , но так как
, но так как 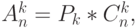 то
то
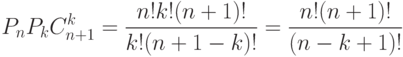
Это возможно лишь при условии , что 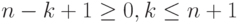
Задача 2. Строится лестница из точки  в точку
в точку 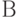 . Расстояние
. Расстояние 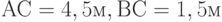 . Высота ступеньки 0,3м , ширина - 0,5м или кратное 0,5 (
рис.
8.1). Сколькими способами можно построить лестницу ?
. Высота ступеньки 0,3м , ширина - 0,5м или кратное 0,5 (
рис.
8.1). Сколькими способами можно построить лестницу ?
Из условия видно, что лестница должна иметь 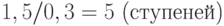 , при этом имеется 10 мест , где можно устроить ступеньку:
, при этом имеется 10 мест , где можно устроить ступеньку: 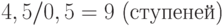 и одна крайняя.
и одна крайняя.
Следовательно, надо выбрать 5 мест для ступеньки из 10: 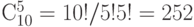 способами.
способами.
Варианты построения показаны на рис. 8.2.
В общем случае: если  ступенек, то лестницу можно построить
ступенек, то лестницу можно построить 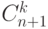 способами.
способами.
Эта задача похожа на предыдущую; укротитель не может ставить двух тигров, а строитель - делать ступеньки удвоенной высоты. Но есть существенное различие: все звери разные, а ступеньки одинаковые, поэтому выбор у строителя меньше.
Обобщением задачи о лестнице (лестницу зашифровать 1 и 0..... ) может быть следующее: сколькими способами можно расставить  нулей и
нулей и  единиц , чтобы две единицы не стояли рядом.
единиц , чтобы две единицы не стояли рядом.
Это можно сделать 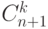 способами.
способами.
Ограничения на порядок выбора
Задача 1. На книжной полке стоят 12 книг. Сколькими способами можно выбрать 5 из них так, чтобы никакие две из них не стояли рядом.
Зашифруем выбор 0 и 1: каждой оставленной книге поставим в соответствие 0, каждой выбранной - 1. Таким образом, имеем 5 единиц и 7 нулей и задача сводится к предыдущей.

В общем виде: Если стоит  книг, а выбирается
книг, а выбирается  книг, не стоящих рядом, то это можно сделать
книг, не стоящих рядом, то это можно сделать
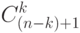
Задача 2. За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует с соседом . Надо выбрать 5 рыцарей (например в экспедицию ,чтобы освободить заколдованную принцессу), причем так, чтобы среди них не было враждующих. ( рис. 8.3) Сколькими способами это можно сделать?
Отличие от предыдущей задачи состоит в том, что рыцари сидят не в ряд, а по кругу. Но ее легко свести к случаю, когда рыцари сидят в ряд. Для этого возьмем рыцаря, например сэра Ланселота, и разомкнем круг. Все выбираемые комбинации распадаются на два класса: в одном участвует сэр Ланселот, в другом - нет. Подсчитаем сколько комбинаций входит в каждый класс.
-
Если сэр Ланселот отправился в поход , то его соседи справа и слева не должны участвовать. Остаются 9 рыцарей из которых надо выбрать 4. Надо проследить, чтобы среди выбранных не было врагов, то есть чтобы никакие двое не сидели рядом. Цепь разорвана следовательно:

-
Так как сэр Ланселот не участвует в экспедиции, то его можно исключить, остается 11 рыцарей, из которых выбирается 5.
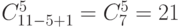 . По правилу суммы всего
. По правилу суммы всего 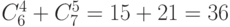 .
.
В общем случае, если по кругу расположены  элементов, а надо выбрать
элементов, а надо выбрать  так , чтобы в их число не попали два соседа , то это можно сделать
так , чтобы в их число не попали два соседа , то это можно сделать 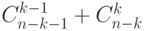 способами.
способами.
Это доказывается точно так же , как и выше . Все комбинации элементов разбиваются на два класса в зависимости от одного из них (сэра Ланселота). В первом варианте будет 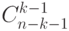 комбинаций , а во втором
комбинаций , а во втором 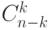 . Легко проверяется , что
. Легко проверяется , что 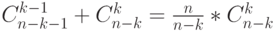
Доказательство:
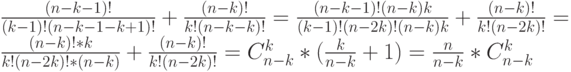 , ч. т. д.
, ч. т. д.




