Алгоритмы: структурированные программы
Что такое алгоритм?
Первоначальной целью теории алгоритмов является классификация всех задач на
алгоритмически разрешимые и неразрешимые, т.е. на те, для которых
существуют решающие их алгоритмы, и те, для которых таких алгоритмов нет.
Неформально под алгоритмом 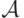 можно понимать выраженный
в некотором языке набор правил (предписание, рецепт, способ),
позволяющий применить к исходным (входным) данным x из некоторого
множества допустимых данных X последовательность дискретных действий
(операций, команд), приводящую к определенному результату - выходным данным
можно понимать выраженный
в некотором языке набор правил (предписание, рецепт, способ),
позволяющий применить к исходным (входным) данным x из некоторого
множества допустимых данных X последовательность дискретных действий
(операций, команд), приводящую к определенному результату - выходным данным  из некоторого множества Y.
В этом случае говорят, что алгоритм
из некоторого множества Y.
В этом случае говорят, что алгоритм 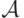 вычисляет функцию
вычисляет функцию  типа X -> Y.
Это нестрогое определение вполне подходит в тех
случаях, когда для некоторой функции нам предъявляется "объект",
называемый алгоритмом ее вычисления (например, алгоритм Эвклида
для вычисления наибольшего общего делителя двух целых чисел),
и можно легко проверить, позволяет ли он действительно вычислить требуемую
функцию. Однако оно совершенно не годится для доказательства того, что
для заданной функции никакого алгоритма нет.
типа X -> Y.
Это нестрогое определение вполне подходит в тех
случаях, когда для некоторой функции нам предъявляется "объект",
называемый алгоритмом ее вычисления (например, алгоритм Эвклида
для вычисления наибольшего общего делителя двух целых чисел),
и можно легко проверить, позволяет ли он действительно вычислить требуемую
функцию. Однако оно совершенно не годится для доказательства того, что
для заданной функции никакого алгоритма нет.
Начиная с тридцатых годов ХХ века, был предпринят ряд исследований для
формализации понятия алгоритма. Перечислим некоторые из предложенных
разными авторами в разное время формальных
моделей: машины Тьюринга-Поста, частично-рекурсивные функции (Гедель, Клини),  -исчисление (Черч, Клини), итеративные автоматы Неймана,
нормальные алгорифмы Маркова,
счетчиковые автоматы Минского, автоматы на графах Колмогорова-Барздиня и др.
Заложенные в них идеи в значительной степени повлияли затем на архитектуру и
языки программирования реальных компьютеров (например, на базе
-исчисление (Черч, Клини), итеративные автоматы Неймана,
нормальные алгорифмы Маркова,
счетчиковые автоматы Минского, автоматы на графах Колмогорова-Барздиня и др.
Заложенные в них идеи в значительной степени повлияли затем на архитектуру и
языки программирования реальных компьютеров (например, на базе  -исчисления
построен широко применяемый в задачах искусственного интеллекта язык ЛИСП,
а из нормальных алгорифмов Маркова произошел хорошо подходящий для
текстовой обработки язык РЕФАЛ). Каждый из многочисленных языков
программирования также
задает некоторую формальную модель алгоритмов. Мы вначале рассмотрим один из
простейших таких языков - простые структурированные программы.
А затем сравним их с двумя
другими моделями алгоритмов: описаниями частично рекурсивных функций и машинами Тьюринга.
-исчисления
построен широко применяемый в задачах искусственного интеллекта язык ЛИСП,
а из нормальных алгорифмов Маркова произошел хорошо подходящий для
текстовой обработки язык РЕФАЛ). Каждый из многочисленных языков
программирования также
задает некоторую формальную модель алгоритмов. Мы вначале рассмотрим один из
простейших таких языков - простые структурированные программы.
А затем сравним их с двумя
другими моделями алгоритмов: описаниями частично рекурсивных функций и машинами Тьюринга.
Хотя алгоритмы в разных прикладных областях имеют дело с дискретными объектами различных видов: целыми и рациональными числами, строками, формулами, разного рода выражениями, графами, матрицами, таблицами, точечными изображениями и др., мы в этой части курса будем рассматривать только задачи вычисления функций от натуральных аргументов, принимающих натуральные значения. Такие функции часто называют арифметическими. Дело в том, что для любого естественного множества дискретных объектов (в частности, для всех перечисленных выше) имеется простое кодирование его элементов целыми числами. Поэтому задачи вычисления функций на этих множествах превращаются в задачи вычисления арифметических функций.
Напомним, что через N обозначается
множество натуральных чисел, т.е. N={0,1,2,...}.
Для частичной n - местной арифметической функции f: Nn -> N через 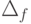 обозначим область ее определения. Чтобы указать, что f не определена
на некотором наборе чисел a1,..., an будем писать
обозначим область ее определения. Чтобы указать, что f не определена
на некотором наборе чисел a1,..., an будем писать 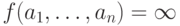 ,
а если f на этом наборе определена, то будем писать
,
а если f на этом наборе определена, то будем писать 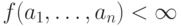 .
Таким образом,
.
Таким образом, 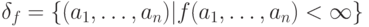 .
.
Структурированные программы
В этом разделе рассмотрим в качестве средства описания алгоритмов структурированные программы. Они вычисляют функции, используя минимальные средства: элементарные присваивания, условные операторы и циклы.
Определим вначале синтаксис структурированных программ. Зафиксируем для этого некоторое счетное множество имен переменных Var, которые будут использоваться в программах. Как обычно, будем считать, что оно включает имена x, x1,x2,..., y, y1,..., z,z1,... и т.п. В последующих определениях x, y, z - это произвольные переменные из Var.
Определение 7.1. Оператор присваивания. Присваивание - это выражение одного из следующих трех видов:
- x := x+1
- x := 0
- x := y.
Определение 7.2. Условия. Условие - это выражение одного из двух видов:
а) x = y или б) x < y.
Структурированные программы определяются индуктивно.
Определение 7.3. Структурированные программы.
- Каждое присваивание - это структурированная программа.
- Если
 и
и 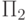 - структурированные программы, то и
- структурированные программы, то и 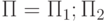 - это структурированная программа.
- это структурированная программа. -
Если
 и
и 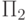 - структурированные программы, а
- структурированные программы, а  - это условие, то
- это условие, то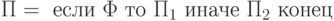
-
Если
 - структурированная программа, а
- структурированная программа, а  - это условие, то
- это условие, то
- Других структурированных программ нет.
Конструкция в п. (б) называется последовательным применением или композицией программ  и
и 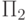 , конструкция в п. (в)
называется условным оператором ; конструкция в п.
(г) - это оператор цикла,
, конструкция в п. (в)
называется условным оператором ; конструкция в п.
(г) - это оператор цикла,  - условие цикла, а
- условие цикла, а  - тело цикла.
- тело цикла.
С помощью структурированных программ (далее называемых просто программами)
вычисляются (частичные) функции от натуральных аргументов, принимающие натуральные
значения. С каждой программой  свяжем естественным образом
множество входящих в нее переменных
свяжем естественным образом
множество входящих в нее переменных 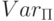 (определите это множество индукцией по построению программы).
В процессе работы программа изменяет значения этих переменных. Операционная семантика задает правила такого изменения.
(определите это множество индукцией по построению программы).
В процессе работы программа изменяет значения этих переменных. Операционная семантика задает правила такого изменения.
Определение 7.4. Состояние - это отображение  из множества переменных Var во множество N.
Для
из множества переменных Var во множество N.
Для 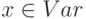 через
через 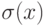 обозначим значение переменной x в состоянии
обозначим значение переменной x в состоянии 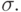 Через S обозначим множество всех состояний.
Через S обозначим множество всех состояний.
Разумеется, при рассмотрении конкретной программы  нас будут интересовать значения переменных из
нас будут интересовать значения переменных из 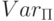 .
.
Определение 7.5. Операционная семантика программы  - это отбражение (вообще говоря, частичное) типа S -> S, которое программа
- это отбражение (вообще говоря, частичное) типа S -> S, которое программа  индуцирует на множестве всех состояний. Через
индуцирует на множестве всех состояний. Через  обозначим состояние - результат применения программы
обозначим состояние - результат применения программы  к состоянию
к состоянию  .
Оно определяется индукцией по построению программы.
.
Оно определяется индукцией по построению программы.
-
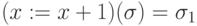 , где
, где 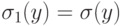 при
при 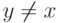 , и
, и 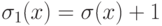 .
. -
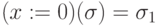 , где
, где 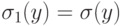 при
при 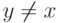 , и
, и 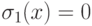 .
. -
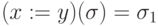 , где
, где 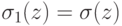 при
при  , и
, и 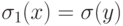
- Пусть
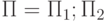 . Тогда
. Тогда 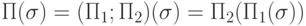 , при этом, если
, при этом, если 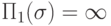 или
или 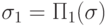 и
и 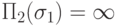 , то и
, то и 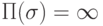 .
. -
Пусть
 если x = y то
если x = y то  иначе
иначе 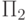 конец. Тогда
конец. Тогда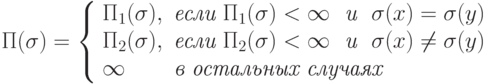
-
Пусть
 если x < y то
если x < y то  иначе
иначе 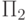 конец. Тогда
конец. Тогда
- Пусть
 пока x = y делай
пока x = y делай  все. Тогда при
все. Тогда при 
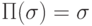 , а при
, а при  - это первое такое состояние
- это первое такое состояние 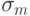 в последовательности состояний
в последовательности состояний 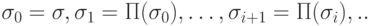 ., что при i <= m все состояния
., что при i <= m все состояния 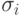 определены, при i <m имеет место
определены, при i <m имеет место  , и
, и 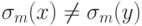 .
. - Семантику для цикла с условием x < y определите самостоятельно (см. задачу 7.1).
Пусть  - программа,
- программа, 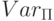 - множество ее переменных. Выделим среди эти переменных некоторое подмножество входных переменных x1,..., xn и одну результирующую (выходную) переменную y (она может быть одной из входных). Переменные из
- множество ее переменных. Выделим среди эти переменных некоторое подмножество входных переменных x1,..., xn и одну результирующую (выходную) переменную y (она может быть одной из входных). Переменные из 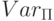 , не являющиеся входными,
будем называть вспомогательными.
, не являющиеся входными,
будем называть вспомогательными.
