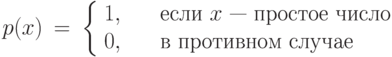Алгоритмы: структурированные программы
Определение 7.6.
Программа  с входными переменными x1,..., xn и результирующей переменной y вычисляет частичную функцию F: n -> ,
если для любого набора значений аргументов
с входными переменными x1,..., xn и результирующей переменной y вычисляет частичную функцию F: n -> ,
если для любого набора значений аргументов 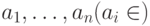 ,
она переводит начальное состояние
,
она переводит начальное состояние 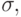 в котором
в котором 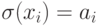 при 1<= i<= n и
при 1<= i<= n и 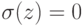 при
при  ,
в состояние
,
в состояние 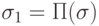 тогда и только тогда, когда
тогда и только тогда, когда 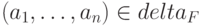 и
и 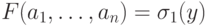 .
.
Функцию, вычисляемую программой  с входными переменными x1,..., xn в (результирующей) переменной y, обозначим
с входными переменными x1,..., xn в (результирующей) переменной y, обозначим 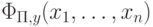 .
.
Арифметическая функция F(x1, ..., xn) программно вычислима, если
она вычислима некоторой программой  в некоторой переменной y
при некотором разбиении переменных
в некоторой переменной y
при некотором разбиении переменных 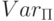 на входные: x1,..., xn
и вспомогательные.
на входные: x1,..., xn
и вспомогательные.
Заметим, что в нашем языке нет понятия процедуры (подпрограммы).
Для сокращения записи мы будем иногда использовать имя одной
ранее написанной программы внутри текста другой: 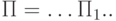 . Такая запись будет означать текстовую (in-line) подстановку текста (кода) программы
. Такая запись будет означать текстовую (in-line) подстановку текста (кода) программы  в соответствующее место программы
в соответствующее место программы  Подчеркнем, что при этом переменные
Подчеркнем, что при этом переменные  не переименовываются и программист сам должен заботиться о правильной инициализации переменных из
не переименовываются и программист сам должен заботиться о правильной инициализации переменных из 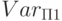 .
Например, если
.
Например, если  использует отдельно написанную программу
использует отдельно написанную программу 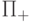 из приведенного ниже примера 7.3 для сложения переменных a и b и получения результата в t, то "безопасный" и корректный способ
сделать это может выглядеть так:
из приведенного ниже примера 7.3 для сложения переменных a и b и получения результата в t, то "безопасный" и корректный способ
сделать это может выглядеть так:
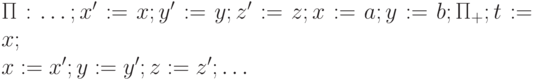
т.е. вначале сохраняются текущие значения переменных x,y,z,
используемых в 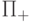 , затем входным переменным x и y присваиваются
нужные значения a и b и вызывается
, затем входным переменным x и y присваиваются
нужные значения a и b и вызывается 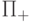 , ее результат передается в t,
затем восстанавливаются значения x,y,z.
, ее результат передается в t,
затем восстанавливаются значения x,y,z.
Рассмотрим несколько примеров программ.
Пример 7.1.
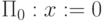
Ясно, что  тождественно равна 0.
тождественно равна 0.
Пример 7.2.
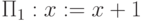
А здесь  для любого x.
для любого x.
Пример 7.3.
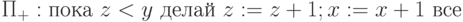
Зафиксируем входные переменные x, y и выходную переменную x
( z - рабочая переменная ). Легко показать, что 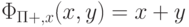 .
.
Действительно, при y=0 тело цикла не выполняется и выход равен x=x+0. При y >= 1 тело цикла выполняется y раз и при каждом его выполнении x увеличивается на 1.
Пример 7.4.
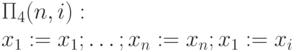
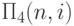 вычисляет в x1 функцию
выбора i-го аргумента:
вычисляет в x1 функцию
выбора i-го аргумента: 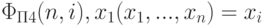 .
.
Пример 7.5.
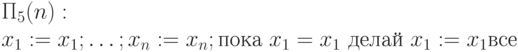
Нетрудно понять, что 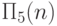 вычисляет нигде не определенную
функцию от n переменных:
вычисляет нигде не определенную
функцию от n переменных: 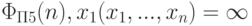 .
.
Задачи
Задача 7.1. Определите (по аналогии с п. (ж)) определения 7.5 семантику для программ вида
 пока x < y делай
пока x < y делай  все.
все.
Задача 7.2.Построить структурированные программы, вычисляющие в z следующие функции, и доказать их корректность:
- f{x}(x,y)= x*y;
- ffact(x)= x!;
-
f-1(x)= x
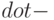 1, где 0
1, где 0 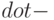 1 = 0 и (x+1)
1 = 0 и (x+1) 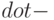 1 = x ;
1 = x ; -
f-(x,y)= x
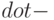 y, где x
y, где x 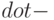 y = x-y, если x >= y и x
y = x-y, если x >= y и x 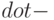 y=0, если x < y ;
y=0, если x < y ; - fsqr(x)= [sqrt x];
- fexp(x)= 2x;
- flog(x)= [log2x];
- f/(x,y)= [x/y].
Задача 7.3.
Пусть  - структурированная программа и
- структурированная программа и 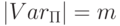 . Из определений
следует, что при различной фиксации входных переменных и выходной переменной
программа может вычислять различные функции.
. Из определений
следует, что при различной фиксации входных переменных и выходной переменной
программа может вычислять различные функции.
- Каково максимальное число функций от n <= m переменных, которое может вычислять
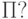 Сколько всего разных функций может вычислить
Сколько всего разных функций может вычислить 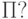
- Постройте программу
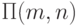 , которая вычисляет максимальное число различных функций от n <= m переменных.
, которая вычисляет максимальное число различных функций от n <= m переменных. - Постройте программу
 с
с 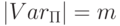 , которая для каждого n <= m вычисляет максимальное число различных функций от n переменных.
, которая для каждого n <= m вычисляет максимальное число различных функций от n переменных.
Задача 7.4.Построить структурированные программы, вычисляющие в z следующие функции:
Задача 7.5.
Пусть структурированная программа  вычисляет в переменной y некоторую всюду определенную взаимно однозначную функцию f(x), область значений которой
совпадает с множеством всех натуральных чисел N. Пусть
вычисляет в переменной y некоторую всюду определенную взаимно однозначную функцию f(x), область значений которой
совпадает с множеством всех натуральных чисел N. Пусть 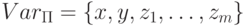 .
Постройте структурированную программу, которая вычисляет
обратную функцию f-1(x) = { z | f(z)=x}.
.
Постройте структурированную программу, которая вычисляет
обратную функцию f-1(x) = { z | f(z)=x}.
Задача 7.6. Пусть F(x) задана соотношениями F(0)=1, F(1)=1, F(x+2)= F(x)+F(x+1) (элементы последовательности F(x) называются числами Фибоначчи). Постройте структурированную программу, которая вычисляет функцию F(x).

![\begin{array}{lll}
f_1(x, y)& =& \left \{\begin{array}{ll}
x^2y^3, & \text{ если $x < y$ } \\
\text{}
[ (x+y)/2 ] , & \text{ в противном случае}
\end{array} \right. \\
\end{array}](/sites/default/files/tex_cache/c8976ac887a50feabaad4a9a1eb5f161.png)
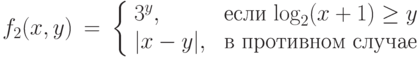
![\begin{array}{lll}
f_3(x, y) &=& \left \{\begin{array}{ll}
[x*y/2], & \text{ если $\log_2 x \leq y+2$ }\\
x^{[y/2], & \mbox{ в противном случае}
\end{array} \right. \\
\end{array}](/sites/default/files/tex_cache/bc78d4a5d9e2bcf001c67f67cbdbc2e1.png)