Конечные автоматы: преобразователи и распознаватели
Пример 4.4. Рассмотрим язык L, состоящий из всех слов в алфавите 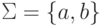 ,
которые начинаются на aa и содержат нечетное число символов b.
,
которые начинаются на aa и содержат нечетное число символов b.
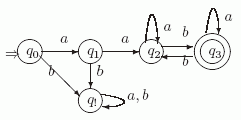
Для выделения слов, начинающихся на aa, создадим начальное состояние q0, которое первый символ a будет переводить в состояние q1, а второй символ a будет переводить q1 в состояние q2. Ясно, что все слова, которые начинаются на ab, ba, bb, сами не входят в язык L и все их продолжения также ошибочны. Заведем для них "ошибочное" состояние q!. Остальные слова естественно разбиваются на два класса: те, в которых четное число символов b, и те, в которых число таких символов нечетно (они и принадлежат L ).
Так как после получения aa число b четно, то для представления слов первого
класса будем использовать состояние q2, а для представления слов второго - создадим состояние q3, которое и будет заключительным. В результате получаем автомат, диаграмма которого
представлена на рис. 4.2. (Мы отмечаем на рисунках диаграмм начальное состояние стрелкой 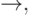 а заключительные состояния - двумя окружностями).
а заключительные состояния - двумя окружностями).
Проверим работу этого автомата, например, на входном слове w=aaababa. При его чтении порождается следующая последовательность конфигураций:
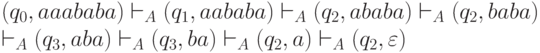
Заключительное состояние этого вычисления q2 не является заключительным.
Следовательно, 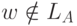 . Если же мы рассмотрим в качестве входа слово w1= w b= aaababab, то, продолжив на один шаг приведенное выше вычисление,
получим, что
. Если же мы рассмотрим в качестве входа слово w1= w b= aaababab, то, продолжив на один шаг приведенное выше вычисление,
получим, что  . Следовательно,
. Следовательно, 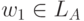 .
.
Мы проверили, что на двух входах автомат A работает верно. Как установить, что он построен корректно, т.е. верно работает на всех входных словах и распознает L? Типичная схема доказательства правильности конечного автомата такова:
- определить (описать) для каждого состояния
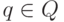 язык L(q), который состоит из слов, переводящих начальное состояние q0 в q ;
язык L(q), который состоит из слов, переводящих начальное состояние q0 в q ; - доказать, что это определение правильное, используя индукцию по длине входного слова ;
- показать, что
 .
.
Применим эту схему к доказательству правильности, построенного выше автомата A. Языки, связанные с состояниями этого автомата, фактически, уже были определены при его построении. Уточним их:

Правильность определения языков L(q0), L(q1) и L(q!) следует непосредственно из определения A. Самое короткое слово, переводящее q0 в q2 - aa, и оно принадлежит L(q2). Аналогично, самое короткое слово, переводящее q0 в q3 - aab, и оно принадлежит L(q3). Предположим теперь, что для каждого слова w длины <= n выполнено условие (*):
w переводит начальное состояние q0 в  .
.
Покажем, что оно будет выполнено и для всех слов длины n +1.
Пусть |w|=n+1. Тогда 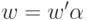 , где
, где 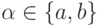 .
Так как |w'|=n, то для w' выполнено условие (*).
Поэтому, если w' переводит q0 в q2, то это слово
начинается с aa и содержит четное число b. При
.
Так как |w'|=n, то для w' выполнено условие (*).
Поэтому, если w' переводит q0 в q2, то это слово
начинается с aa и содержит четное число b. При 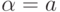 слово w переводит q0 в q2 и также начинается с aa и содержит четное число b,
а при
слово w переводит q0 в q2 и также начинается с aa и содержит четное число b,
а при 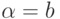 слово w переводит q0 в q3,
начинается с aa и содержит нечетное число b, т.е. принадлежит L.
слово w переводит q0 в q3,
начинается с aa и содержит нечетное число b, т.е. принадлежит L.
Аналогично, если w' переводит q0 в q3, то это слово
начинается с aa и содержит нечетное число b. При 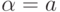 слово w также переводит q0 в q3 и также начинается с aa и содержит нечетное число b,
а при
слово w также переводит q0 в q3 и также начинается с aa и содержит нечетное число b,
а при 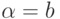 w переводит q0 в q2, оно
начинается с aa и содержит четное число b.
Обратно, если
w переводит q0 в q2, оно
начинается с aa и содержит четное число b.
Обратно, если 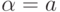 , то слово w переводит q0 в
, то слово w переводит q0 в 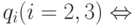 w' переводит q0 в qi\ (i=2,3) и условие (*) выполнено, так как четность числа
букв b в w и в w' одинакова. Если же
w' переводит q0 в qi\ (i=2,3) и условие (*) выполнено, так как четность числа
букв b в w и в w' одинакова. Если же 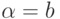 , то из определения автомата A
следует, что слово w переводит q0 в
, то из определения автомата A
следует, что слово w переводит q0 в 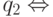 w' переводит q0 в q3 и w переводит q0 в
w' переводит q0 в q3 и w переводит q0 в 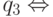 w' переводит q0 в q2.
Так как четность числа букв b в w и в w' разная, то и в этом случае условие (*) выполнено. Для завершения доказательства осталось заметить,
что единственным заключительным состоянием автомата A является q3 и поэтому LA = L(q3) = L.
w' переводит q0 в q2.
Так как четность числа букв b в w и в w' разная, то и в этом случае условие (*) выполнено. Для завершения доказательства осталось заметить,
что единственным заключительным состоянием автомата A является q3 и поэтому LA = L(q3) = L.