|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
Цель лекции: Основной целью лекции является применение полученные знания о разработке и отладке параллельных программ в реализации численных алгоритмов для работы с матрицами.
![]() Видеозапись лекции - (объем - 707 МБ).
Видеозапись лекции - (объем - 707 МБ).
Прямые методы решения СЛАУ
Методы решения систем линейных алгебраических уравнений (СЛАУ) относятся к численным методам алгебры. При формальном подходе решение подобных задач не встречает затруднений: решение системы можно найти, раскрыв определители в формуле Крамера.
Однако при непосредственном раскрытии определителей решение системы с n неизвестными требует 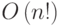 арифметических операций; уже при n порядка 20 такое число операций недоступно для современных компьютеров.
При сколько-нибудь больших n применение методов с таким порядком числа операций будет невозможно и в обозримом будущем. Другой причиной, по которой этот классический способ неприменим даже при малых n, является сильное влияние на окончательный результат округлений при вычислениях.
арифметических операций; уже при n порядка 20 такое число операций недоступно для современных компьютеров.
При сколько-нибудь больших n применение методов с таким порядком числа операций будет невозможно и в обозримом будущем. Другой причиной, по которой этот классический способ неприменим даже при малых n, является сильное влияние на окончательный результат округлений при вычислениях.
Методы решения алгебраических задач можно разделить на точные и итерационные. Классы задач, для решения которых обычно применяют методы этих групп, можно условно назвать соответственно классами задач со средним и большим числом неизвестных. Изменение объема и структуры памяти вычислительных систем, увеличение их быстродействия и развитие численных методов приводят к смещению границ применения методов в сторону систем более высоких порядков.
Например, в 80-х годах прошлого века точные методы применялись для решения систем до порядка 104, итерационные – до порядка 107, в 90-х – до порядков 105 и 108 соответственно. Современные суперкомпьютеры способны использовать точные методы при решении еще больших систем.
Мы будем рассматривать систему из n линейных алгебраических уравнений вида
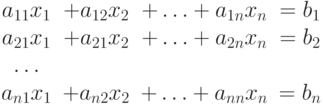 |
( 7.1) |
В матричном виде система может быть представлена как
 |
( 7.2) |
где 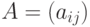 есть вещественная матрица размера
есть вещественная матрица размера  ; b и x - вектора из n элементов.
; b и x - вектора из n элементов.
Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b мы будем считать нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.
Метод исключения Гаусса
В первую очередь рассмотрим алгоритмыы, предназначенные для решения системы
 |
( 7.3) |
с произвольной квадратной матрицей А. Основой для всех них служит широко известный метод последовательного исключения неизвестных, или же метод Гаусса.
Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решение рассматриваемой системы (такие преобразования носят наименование эквивалентных). К числу таких преобразований относятся:
- умножение любого из уравнений на ненулевую константу,
- перестановка уравнений,
- прибавление к уравнению любого другого уравнения системы.
Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе, который называется прямой ход, исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду. При выполнении обратного хода (второй этап алгоритма) осуществляется определение значений неизвестных.
Последовательный алгоритм
Прямой ход состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений.
На итерации i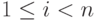 , метода производится исключение неизвестной i для всех уравнений с номерами k, больших i(т.е.
, метода производится исключение неизвестной i для всех уравнений с номерами k, больших i(т.е.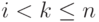 ) Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу
) Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу 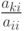 с тем, чтобы результирующий коэффициент при неизвестной
с тем, чтобы результирующий коэффициент при неизвестной 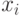 в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:
в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:
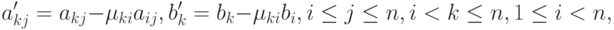 |
( 7.4) |
где 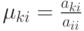 - множители Гаусса.
- множители Гаусса.
В итоге приходим к системе 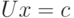 с верхней треугольной матрицей
с верхней треугольной матрицей
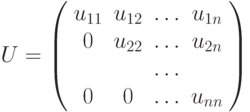
При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Как можно заметить, выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент

Избежать подобной проблемы можно, если при выполнении каждой очередной итерации прямого хода метода Гаусса определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.е.
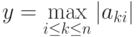
и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).
Обратный ход алгоритма состоит в следующем. После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной
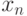
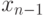
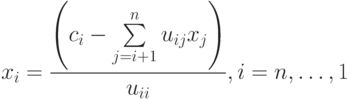
Оценим трудоемкость метода Гаусса. При выполнении прямого хода число операций составит
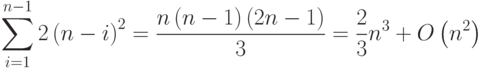
Для выполнения обратного хода потребуется
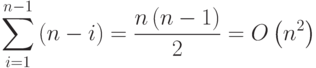
Таким образом, общее время выполнения метода Гаусса при больших n можно оценить как
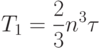
где  время выполнения одной операции.
время выполнения одной операции.
Параллельный алгоритм
При внимательном рассмотрении метода Гаусса можно заметить, что все вычисления сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Как результат, в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять тогда все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b. Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами.
Для выполнения прямого хода метода Гаусса необходимо осуществить 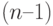 итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду. Выполнение итерации i,
итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду. Выполнение итерации i,  , прямого хода метода Гаусса включает ряд последовательных действий. Прежде всего, в самом начале итерации необходимо выбрать ведущую строку, которая при использовании метода главных элементов определяется поиском строки с наибольшим по абсолютной величине значением среди элементов столбца i, соответствующего исключаемой переменной
, прямого хода метода Гаусса включает ряд последовательных действий. Прежде всего, в самом начале итерации необходимо выбрать ведущую строку, которая при использовании метода главных элементов определяется поиском строки с наибольшим по абсолютной величине значением среди элементов столбца i, соответствующего исключаемой переменной  . Зная ведущую строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной
. Зная ведущую строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной  .
.
При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i,  , определяет значение своей переменной
, определяет значение своей переменной  , это значение должно быть использовано всеми подзадачам с номерами k,
, это значение должно быть использовано всеми подзадачам с номерами k,  : подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.
: подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.
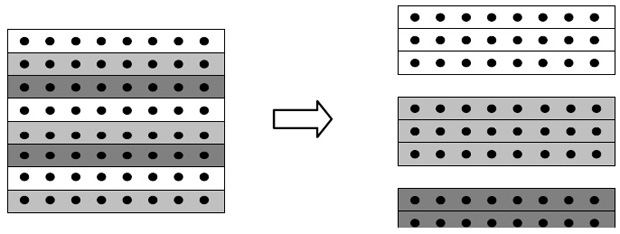
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью. Однако размер матрицы, описывающей систему линейных уравнений, является существенно большим, чем число потоков в программе (т.е., ), и базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько строк матрицы. При этом применение последовательной схемы разделения данных для параллельного решения систем линейных уравнений приведет к неравномерной вычислительной нагрузке между потоками: по мере исключения (на прямом ходе) или определения (на обратном ходе) неизвестных в методе Гаусса для большей части потоков все необходимые вычисления будут завершены и они окажутся простаивающими. Возможное решение проблемы балансировки вычислений может состоять в использовании ленточной циклической схемы для распределения данных между укрупненными подзадачами. В этом случае матрица A делится на наборы (полосы) строк вида
(см. рис. 7.1).
), и базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько строк матрицы. При этом применение последовательной схемы разделения данных для параллельного решения систем линейных уравнений приведет к неравномерной вычислительной нагрузке между потоками: по мере исключения (на прямом ходе) или определения (на обратном ходе) неизвестных в методе Гаусса для большей части потоков все необходимые вычисления будут завершены и они окажутся простаивающими. Возможное решение проблемы балансировки вычислений может состоять в использовании ленточной циклической схемы для распределения данных между укрупненными подзадачами. В этом случае матрица A делится на наборы (полосы) строк вида
(см. рис. 7.1).
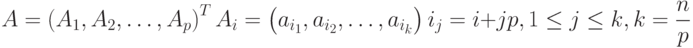
Сопоставив схему разделения данных и порядок выполнения вычислений в методе Гаусса, можно отметить, что использование циклического способа формирования полос позволяет обеспечить лучшую балансировку вычислительной нагрузки между подзадачами.
Итак, проведя анализ последовательного варианта алгоритма Гаусса, можно заключить, что распараллеливание возможно для следующих вычислительных процедур:
- поиск ведущей строки,
- вычитание ведущей строки из всех строк, подлежащих обработке,
- выполнение обратного хода.
Оценим трудоемкость рассмотренного параллельного варианта метода Гаусса. Пусть n есть порядок решаемой системы линейных уравнений, а p,  , обозначает число потоков. При разработке параллельного алгоритма все вычислительные операции, выполняемые алгоритмом Гаусса, были распределены между потоками параллельной программы. Следовательно, время, необходимое для выполнения вычислений на этапе прямого хода, можно оценить как
, обозначает число потоков. При разработке параллельного алгоритма все вычислительные операции, выполняемые алгоритмом Гаусса, были распределены между потоками параллельной программы. Следовательно, время, необходимое для выполнения вычислений на этапе прямого хода, можно оценить как
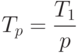
Подставив выражение  получим, что время выполнения вычислений для параллельного варианта метода Гаусса описывается выражением:
получим, что время выполнения вычислений для параллельного варианта метода Гаусса описывается выражением:
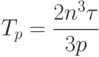
Теперь можно оценить величину накладных расходов, обусловленных организацией и закрытием параллельных секций. Пусть  – время, необходимое на организацию и закрытие параллельной секции. Параллельная секция создается при каждом выборе ведущей строки, при выполнении вычитания ведущей строки из остальных строк линейной системы, подлежащих обработке, а также при выполнении каждой итерации обратного хода метода Гаусса. Таким образом, общее число параллельных секций составляет
– время, необходимое на организацию и закрытие параллельной секции. Параллельная секция создается при каждом выборе ведущей строки, при выполнении вычитания ведущей строки из остальных строк линейной системы, подлежащих обработке, а также при выполнении каждой итерации обратного хода метода Гаусса. Таким образом, общее число параллельных секций составляет  .
.
Сводя воедино все полученные оценки можно заключить, что время выполнения параллельного метода Гаусса описывается соотношением
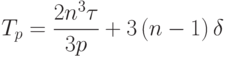 |
( 7.5) |
Связь метода Гаусса и LU-разложения
LU-разложение - представление матрицы A в виде
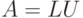 |
( 7.6) |
где L - нижняя треугольная матрица с диагональными элементами, равными единице, а U - верхняя треугольная матрица с ненулевыми диагональными элементами. LU-разложение также называют LU-факторизацией. Известно [4], что LU-разложение существует и единственно, если главные миноры матрицы A отличны от нуля.
Алгоритм LU-разложения тесно связан с методом исключения Гаусса. В самом деле, пусть мы решаем систему уравнений вида (7.2). Непосредственно проверяется, что преобразования k-го шага метода Гаусса равносильны домножению системы (7.2) слева на матрицу
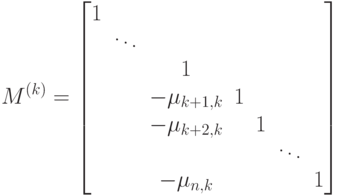
где 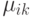 - множители Гаусса из (7.4). Как было рассмотрено в п. 7.1.1, прямой ход метода Гаусса преобразует исходную систему уравнений к виду
- множители Гаусса из (7.4). Как было рассмотрено в п. 7.1.1, прямой ход метода Гаусса преобразует исходную систему уравнений к виду
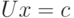
с верхней треугольной матрицей U. Зная матрицы 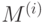 , можно записать матрицу U и вектор c как
, можно записать матрицу U и вектор c как
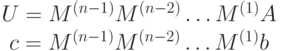
Обозначим 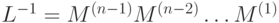 Можно непосредственно проверить, что
Можно непосредственно проверить, что
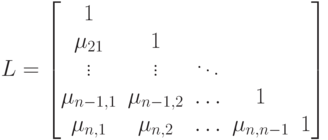
Отсюда получаем 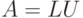 .
.
Таким образом, матрицу L можно получить как нижнюю треугольную матрицу коэффициентов Гаусса, а матрицу U - как верхнюю треугольную матрицу, получаемую в результате работы метода Гаусса. При этом очевидно, что трудоемкость получения LU-факторизации будет такой же-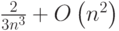 .
.
Рассмотренный нами алгоритм LU-факторизации реализован с помощью исключения по столбцу. Следует отметить, что можно сформулировать аналогичный алгоритм, основанный на исключении по строке. В самом деле, основная идея алгоритма с помощью исключения по столбцу заключается в том, что на i-й итерации ведущая строка с подходящими множителями вычитается из строк, лежащих ниже, чтобы занулить все элементы матрицы, расположенные в i-м столбце ниже диагонали. Между тем возможно и другое: на каждой i-й итерации можно вычитать из i-й строки все строки, расположенные выше, умноженные на подходящие коэффициенты, так, чтобы занулить все элементы i-й строки левее диагонали. При этом элементы матрицы L ниже главной диагонали и элементы матрицы U на главной диагонали и выше нее можно вычислять на месте матрицы А. Как и в случае исключения по столбцу, приведенная схема требует проведения 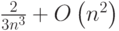 операций
операций
Рассмотрим теперь еще один способ LU-факторизаци, называемый компактной схемой. Пусть матрица 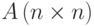 допускает LU-разложение (7.6), где
допускает LU-разложение (7.6), где
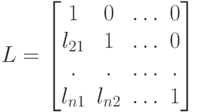

т.е.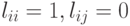 при
при 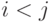 а
а 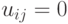 при
при  . Из соотношения (7.6) следует, что
. Из соотношения (7.6) следует, что
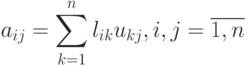
Преобразуем эту сумму двумя способами:
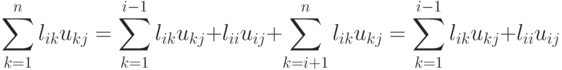
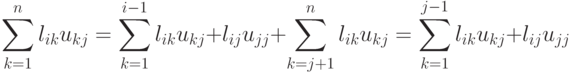
Отсюда находим
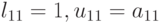
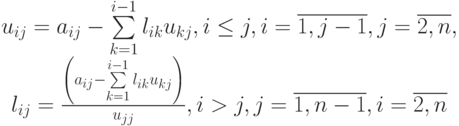
Оценка числа операций данного алгоритма LUфакторизаци также составляет
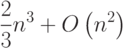
Если разложение (7.6) получено, то решение системы (7.2) сводится к последовательному решению двух систем уравнений с треугольными матрицами (обратный ход)
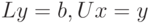 |
( 7.7) |
Обратный ход требует 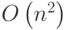 операций.
операций.
Как следует из приведенных оценок, вычислительная сложность метода исключения Гаусса и метода LU-разложения одинакова. Однако если необходимо решить несколько систем с одинаковыми матрицами коэффициентов, но различными векторами свободных членов (правая часть СЛАУ), то метод LU-разложения окажется предпочтительным, так как в этом случае нет необходимости производить разложение матрицы коэффициентов многократно. Достаточно лишь сохранить полученные треугольные матрицы в памяти и, подставляя различные вектора свободных членов, получать решения методами прямой и обратной подстановки. Это позволит значительно сократить объем вычислений по сравнению с методом Гаусса.