| Россия, Магнитогорск |
Особенности вычислительных процедур
Цель лекции: Показать различия вычислительных процедур в классической математике и их реализации на компьютере. Подготовить слушателя к различным особенностям научного программирования.
Вычисления сопровождают человечество с незапамятных времен. И уже в древности человечество стало использовать уравнения. Сейчас в математике используются огромное количество уравнений всех видов. Если посмотреть работы, например, по дифференциальным уравнениям, то можно заметить, что огромная часть работ посвящена доказательствам теорем существования, единственности, гладкости и качественным вопросам поведения решений. При этом вопрос о собственно нахождении решений часто вообще не возникает. А между прочим, уравнения создаются именно для нахождения решений. Ни сколько не умаляя важность теоретического исследования уравнений и свойств их решений, мы обратим внимание на нахождение решения.
Сразу возникает вопрос: а что значит решить уравнение? Что должно являться решением уравнения? Для простейшего линейного уравнения с рациональными коэффициентами - решение есть рациональное число, которое может быть представлено дробью с целыми числами и для нахождения которого необходимо выполнить конечное число операций сложения и умножения целых чисел. А если вспомнить, что умножение есть многократное суммирование, то единственные операции, которые мы должны выполнять - это сложение целых чисел. Сложение целых чисел является конструктивной операцией. Сложить два целых числа может и ребенок и даже механическое устройство. И что самое главное - решение представимо в конечном виде.
Однако уже в древности люди столкнулись с тем, что некоторые очень простые, и взятые из практики, задачи нельзя решить в конечном виде. Примером тому простейшее квадратное уравнение:
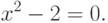 |
( 4.1) |
В тоже время любой (уже не любой, но хороший) школьник знает, что уравнение 4.1 имеет два решения:
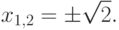
Однако еще Пифагор знал, что длина диагонали квадрата не
соизмерима со стороной, т.е. число 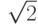 не является
рациональным и не может быть записана в конечном виде. Но так ли
это? Что значить "быть выраженным в конечном виде"? Для нас это
эквивалентно конструктивности объекта. Мы будем предполагать, что
целые числа, операция сложения целых чисел, а также процедура
сравнения двух целых чисел являются конструктивными. Далее
конструктивный объект - это такой объект, который с любой
наперед заданной точностью можно выразить с помощью конечного
числа операций сложения (вычитания) целых чисел.
не является
рациональным и не может быть записана в конечном виде. Но так ли
это? Что значить "быть выраженным в конечном виде"? Для нас это
эквивалентно конструктивности объекта. Мы будем предполагать, что
целые числа, операция сложения целых чисел, а также процедура
сравнения двух целых чисел являются конструктивными. Далее
конструктивный объект - это такой объект, который с любой
наперед заданной точностью можно выразить с помощью конечного
числа операций сложения (вычитания) целых чисел.
Мы подошли к центральному понятию вычислительных процедур - понятию алгоритма. Понятие алгоритма, как последовательность определенных действий, позволяющая за конечное время придти к заданному результату, является не формальным, поэтому в теории алгоритмов используются так называемые уточнения понятия алгоритма. Среди наиболее известных уточнений алгоритма упомянем: частично рекурсивные функции, машины Тьюринга, нормальные алгорифмы Маркова, структурированные программы и др. Смысл уточнения понятия алгоритма состоит в том, чтобы выделить класс задач, которые могут быть решены с помощью идеальных вычислительных машин. Мы будем смотреть на понятие алгоритма с практической точки зрения. Все алгоритмы, которые мы будем рассматривать будут реализованы в виде программ на языке C#. Однако нужно помнить при реализации алгоритмов на языках программирования, что наличие в этих языках переменных типа double отнюдь не означает, что наши программы могут работать с вещественными числами, поскольку тип double может представлять только конечный набор рациональных чисел.
Возвращаясь к числу 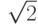 , покажем как записать это число в
конечном виде. Для этого приведем код на языке C#, который
вычисляет значение
, покажем как записать это число в
конечном виде. Для этого приведем код на языке C#, который
вычисляет значение 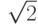 с любой наперед заданной точностью.
с любой наперед заданной точностью.
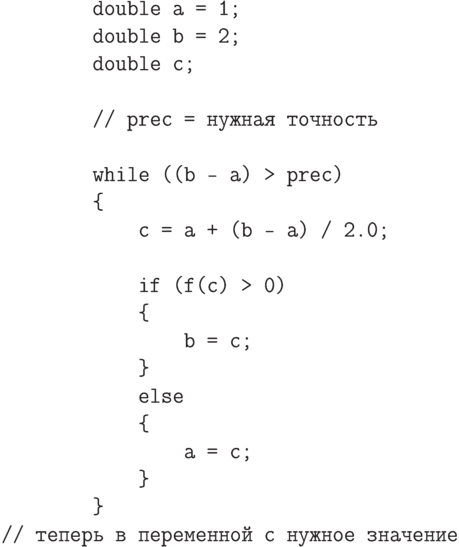
В математике долгое время найти решение означало выписать "аналитически" решение: число или функцию. Однако с возрастающими потребностями инженерных вычислений все большее значения стали приобретать расчеты "вплоть до числа". В этой ситуации, во-первых, для большинства задач не существовало "аналитически выражаемого" решения, а, во-вторых, зачастую нахождение аналитического решения и последующее вычисление конкретных чисел представляло собой не более легкую задачу, чем вычисления приближенного решения.
Однако, если не брать во внимание мифическую разностную машину Ч.Бебиджа, то вычисления производились в ручную (с использованием подручных логарифмических линеек и арифмометров). Следовательно, численные методы разрабатывались как можно более удобно для ручных расчетов. Появление программируемых вычислительных машин кардинально изменило отношение к вычислительным процедурам. С одной стороны открылись огромные возможности численных экспериментов, а с другой перед вычислительной математикой возникли новые проблемы, связанные с машинной точностью.
Проведем небольшой вычислительный эксперимент, который
продемонстрирует существование машинного  . Машинным
. Машинным  называется такое положительное число
называется такое положительное число  , для которого
на рассматриваемой машине является верным утверждение:
, для которого
на рассматриваемой машине является верным утверждение:
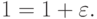
Разумеется, с точки зрения математики существование машинного  является невозможным. Но дело в том, что при реализации на
компьютере банальные арифметические операции не совпадают с
настоящими арифметическими операциями. Это связано с конечностью
представления чисел на компьютере. Приведем код для вычисления
машинного
является невозможным. Но дело в том, что при реализации на
компьютере банальные арифметические операции не совпадают с
настоящими арифметическими операциями. Это связано с конечностью
представления чисел на компьютере. Приведем код для вычисления
машинного  .
.

На моем компьютере машинное 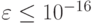 . Наличие машинного
. Наличие машинного  не означает, что невозможно использовать числа меньшие по
модулю. Согласно документации .NET число с типом double может быть
порядка от
не означает, что невозможно использовать числа меньшие по
модулю. Согласно документации .NET число с типом double может быть
порядка от 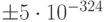 до
до 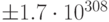 . Но при
выполнении машинных расчетов нужно учитывать машинную арифметику.
. Но при
выполнении машинных расчетов нужно учитывать машинную арифметику.
Чтобы продемонстрировать отличие машиной арифметики рассмотрим следующий пример. Вычислим две величины:
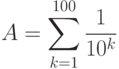
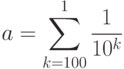
![\begin{verbatim}
class TEps {
double[] ak;
public TEps()
{
ak = new double[101];
ak[0] = 1.0;
for (int k = 1; k <= 100; k++)
{
ak[k] = ak[k - 1] / 1.1;
}
}
public double A()
{
double res = 0;
for (int k = 1; k <= 100; k++)
{
res += ak[k];
}
return res;
}
public double a()
{
double res = 0;
for (int k = 100; k >= 1; k--)
{
res += ak[k];
}
return res;
}
}
\end{verbatim}](/sites/default/files/tex_cache/13ff3796ee096b659679c9306a51f587.png)
Если мы вычислим разницу между величинами A и a, то получим:
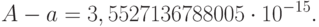
При вычислении сумм всегда нужно суммировать с наименьших по модулю чисел (почему?).
Следующая важная особенность вычислительных процедур - это вычислительная неустойчивость. Как мы уже видели, помимо
погрешностей численных методов в расчетах всегда возникают ошибки
округления. Эти ошибки могут накапливаться в ходе расчетов и
сделать результат вычислений совершенно неверным. Вычислительная
неустойчивость также является препятствием для повышения точности
расчетов. Продемонстрируем это на примере вычисления производной
функции 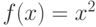 . Мы будем вычислять эту функцию в разных точках
с различным приращением аргумента по естественной формуле:
. Мы будем вычислять эту функцию в разных точках
с различным приращением аргумента по естественной формуле:
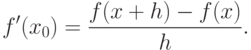 |
( 4.2) |
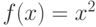 является более чем дифференцируемой в любой
точке, поэтому (теоретически) чем меньше приращение
является более чем дифференцируемой в любой
точке, поэтому (теоретически) чем меньше приращение  тем с
большой точностью мы должны приближаться к значению производной:
тем с
большой точностью мы должны приближаться к значению производной:  .
.А теперь посмотрим как это выглядит на практике. Реализуем эту процедуру:


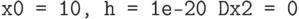
 , поэтому в реальности нашего
приращения попросту не было. Теперь будем осторожнее:
, поэтому в реальности нашего
приращения попросту не было. Теперь будем осторожнее: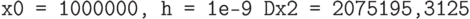
 :
: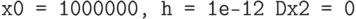

Теперь рассмотрим вопрос об эффективности вычислительных процедур.
Математика не знает оценочных категорий, такие слова "много",
"сложно", "долго" не имеют математического смысла. Однако
когда мы начинаем реализацию вычислительных процедур на реальных
компьютерах, а не на машине Тьюринга, то вопросы эффективности
вычислительных процедуры могут стать принципиальными. Например, с
точки зрения "чистой математики" разложить любое целое число на
простые сомножители не представляет собой никаких проблем -
любое число может быть единственным образом разложено на простые
сомножители, и можно указать алгоритм для этого разложения. Однако
это знание не позволит выполнить такое разложение для больших
чисел. Другой пример представляют собой задачи целочисленного
линейного программирования, в которых необходимо найти минимум
линейной функции на заданном компактном множестве в 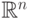 с
целочисленными координатами. Поскольку компактное множество
конечно, то количество точек, на которых необходимо найти минимум,
конечно. Следовательно, можно утверждать существования такого
минимума и с помощью перебора найти точки, на которых этот минимум
достигается. Однако для решения этой задачи разрабатывают
многочисленные методы решения задачи линейного программирования,
пригодные для проведения реальных расчетов. В дискретной
математике изучается большое количество "конечных" задач,
которые теоретическим имеют тривиальное решение путем перебора.
Однако реальность требует разрабатывать оптимальные методы для
решения этих задач.
с
целочисленными координатами. Поскольку компактное множество
конечно, то количество точек, на которых необходимо найти минимум,
конечно. Следовательно, можно утверждать существования такого
минимума и с помощью перебора найти точки, на которых этот минимум
достигается. Однако для решения этой задачи разрабатывают
многочисленные методы решения задачи линейного программирования,
пригодные для проведения реальных расчетов. В дискретной
математике изучается большое количество "конечных" задач,
которые теоретическим имеют тривиальное решение путем перебора.
Однако реальность требует разрабатывать оптимальные методы для
решения этих задач.
Ключевые термины
Алгоритм - последовательность определенных действий, позволяющая за конечное время придти к заданному результату.
Вычислительная неустойчивость - неустойчивость при работе вычислительной процедуры в следствии машинной арифметики.
Конструктивная операция - операция, которая может быть выполнена механически в конечное время и при использовании конечного алфавита.
Машинное  - такое максимальное положительное число
- такое максимальное положительное число  , для
которого на рассматриваемой машине является верным утверждение
, для
которого на рассматриваемой машине является верным утверждение 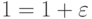 .
.
Краткие итоги: На простых, но естественных примерах показаны особенности вычислительных процедур при их реализации на компьютере. Показаны простейшие методы разработки вычислительных процедур, позволяющие избежать вычислительной неустойчивости.
