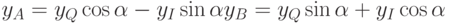НОУ ИНТУИТ | Высокоскоростные сети связи. Лекция 4: Цифровая модуляция

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.05.2012 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 50 студентам

| Поделиться |

Поддержать программу

Реализация демодулятора

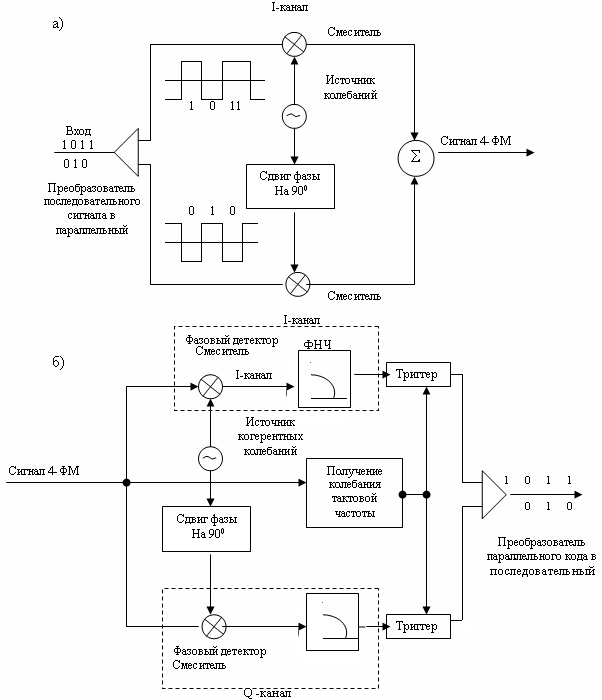
Структура модулятора и демодулятора для 4-ФМ приведена на рис. 4.6 Основной элемент модулятора ФМ – смеситель.

Основными элементами модулятора ФМ являются смеситель и фильтр низкой частоты (ФНЧ).

Рис. 4.6. Структура 4-ФМ модулятора – демодулятора а) – модулятора, б – демодуляторы

Комбинацию смесителя и фильтра низкой частоты (ФНЧ) называют фазовым детектором (ФД). Функции ФД математически выражаются в виде:

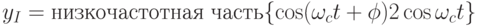$y_I=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\cos\omega_ct\}$

( 4.3)

Для дальнейшего изложения напомним формулы тригонометрических преобразований

$\sin\alpha\sin\beta=\frac 1 2 \left[\cos(\alpha-\beta)-\cos(\alpha+\beta)\right]\\ \cos\alpha\cos\beta=\frac 1 2 \left[\cos(\alpha-\beta)+\cos(\alpha+\beta)\right]\\ \sin\alpha\cos\beta=\frac 1 2 \left[\sin(\alpha-\beta)-\sin(\alpha+\beta)\right]\\ \sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\\ \cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\\ y_I=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\cos\omega_ct\}$

Применяя формулу $\cos\alpha\cos\beta=\frac 1 2 \left[\cos(\alpha-\beta)+\cos(\alpha+\beta)\right]$

Получим $y_I=\text{низкочастотная часть}\{\cos\phi+\cos(2\omega_ct+\phi)\}$

Применяя формулу $\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta$

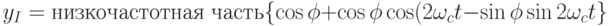
Получим $y_I=\text{низкочастотная часть}\{\cos\phi+\cos\phi\cos(2\omega_ct-\sin\phi\sin2\omega_ct\}$

Отделяя с помощью низкочастотного фильтра, составляющие с удвоенной частотой 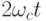$2\omega_ct$ получаем значение:

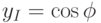
$y_I=\cos\phi$

С помощью тригонометрических преобразований можем получить выходной сигнал Q –канала

$y_Q=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\sin\omega_ct\}=-\sin\phi\\y_Q=-\sin\phi$

Полученные функции могут быть использованы для получения исходного сигнала. Сигнал может быть получен после того, как будет определено значение аргумента $\phi$ .

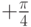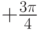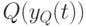В качестве первого примера рассмотрим детектирование сигналов с модуляцией 4 –ФМ, представленных в табл.4.1. Рассмотрение табл.4.1 показывает, что из двух битов данных первый бит, равен при положительном значении фазы сдвига ( $+\frac{\pi}{4}$ и $+\frac{3\pi}{4}$ ), т.е. первый бит полностью определяется отрицательным знаком $\sin\phi$ , т.е. значением сигнала на выходе Q (y_Q(t)) .Значение второго бита равно при фазе сдвига $\pm\frac{\pi}{4}$ , т.е. 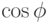полностью определяется положительным знаком, $\cos\phi$ , т.е. выходным сигналом на выходе 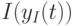I (y_I(t)) . Основной способ реализации демодулятора для 4-ФМ сигналов показан на рис.4.6 . Система 4-ФМ приведена, как основа для описания других способов реализации.

Следует отметить, что в системе 4-ФМ имеются два раздельных потока данных. Модулятор разделяет входящий поток данных таким образом, чтобы биты поочередно отсылались то к синфазному I-модулятору, то к инверсному Q-модулятору. На выходе соответствующего ФД эти биты возникают опять поочередно и вставляются в один поток битов. Таким образом можно говорить о наличии двух независимых двоичных каналов ФМ с ортогональными несущими 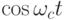$\cos\omega_ct$ и $\sin\omega_ct$ .

Эти каналы называются обычно I и Q каналами. Способ создания таких двух независимых каналов в пределах одной полосы иногда называют квадратурным мультиплексированием.

До тех пор пока в демодуляторе соблюдается ортогональность между несущими в модуляторе и эталонными колебаниями (в приемнике когерентность поддерживается в обоих каналах), каналы I и Q не взаимодействуют между собой. В противном случае малейшие отклонения от ортогональности приводят к взаимным помехам в квадратурных каналах. Взаимные помехи могут быть вызваны несбалансированными фазовыми искажениями в канале передачи.

На первый взгляд может показаться, что при квадратурном мультиплексировании пропускная способность при заданной полосе возрастает в два раза. Но нужно помнить, что сигнал в ФМ сигнал в квадратурном канале представляет собой сигнал с двумя боковыми полосами. Значит, полоса канала без квадратурного сигнала меньше, она составляет 50% полосы системы с одной боковой полосой. При использовании квадратурных каналов работа с одной боковой полосой становится невозможным, так как процесс разделения боковых приводит к нарушению ортогональности двух сигналов. В сущности, квадратурное мультиплексирование только компенсирует потерю пропускной способности, связанную с передачей спектра с двумя боковыми полосами. Демодуляция в системах с большим числом уровней усложнена тем, что использование только двух опорных колебаний не обеспечивает простое детектирование всех битов данных. Существует два основных метода, применяемых для детектирования данных.

Первый состоит в использовании большого числа опорных колебаний в приемнике и измерении фазы принятого сигнала по отношению каждого из дополнительных опорных колебаний. При втором методе используются только два опорных колебания и соответствующие им ФД, а все дополнительные измерения реализуются как линейная комбинация двух ФД.

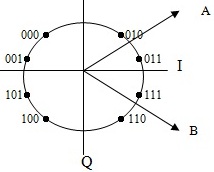
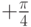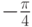В качестве примера первого метода рассмотрим систему с 8-ФМ ( таблица 4.2 и рис. 4.7). Оптимальное детектирование в такой системе может быть достигнуто при наличии двух дополнительных выходных сигналов с ФД с фазами $+\frac{\pi}{4}$ и $-\frac{\pi}{4}$ .Эти два опорных колебания обозначены на рис.4.7 как A и B

Рис. 4.7. Опорные колебания для детектирования сигналов с 8-ФМ

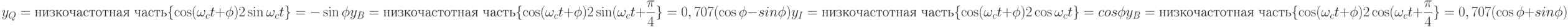$y_Q=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\sin\omega_ct\}=-\sin\phi\\ y_B=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\sin(\omega_ct+\frac{\pi}{4}\}=0,707(\cos\phi-sin\phi)\\ y_I=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\cos\omega_ct\}=cos\phi\\ y_B=\text{низкочастотная часть}\{\cos(\omega_ct+\phi)2\cos(\omega_ct+\frac{\pi}{4}\}=0,707(\cos\phi+sin\phi)\\$

( 4.4)

Для поиска двоичного решения эти выражения рассчитаны и представлены в таблице 4.3

Таблица 4.3. Выходной сигнал фазового детектора 8-ФМ
Данные	Фаза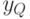
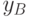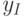011	$\frac{\pi}{8}$	-0,383	0,383	0,924	0,924
010	$\frac{3\pi}{8}$	-0,924	0,383	0,383	0,924
000	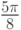$\frac{5\pi}{8}$	-0,924	-0,924	-0,383	0,383
001	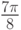$\frac{7\pi}{8}$	-0,383	-0,924	-0,924	-0,383
101	$-\frac{7\pi}{8}$	0,383	-0,383	-0,924	-0,924
100	$-\frac{5\pi}{8}$	0,924	0,383	-0,383	-0,924
110	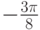$-\frac{3\pi}{8}$	0,924	0,924	0,383	-0,383
111	$-\frac{\pi}{8}$	0,383	0,924	0,924	0,383

Значения в табл. 4.3 показывают, что:

при положительном значении 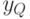первый бит данных всегда равен ,
при положительном значении 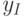второй бит равен ,
третий бит равен если все три значения 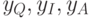имеют один и тот же знак.

Логически можно записать

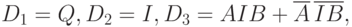
$D_1=Q,D_2=I,D_3=AIB+\overline{A}\,\overline{IB},$

где

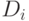- i–тый бит данных;
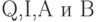$\text{Q,I,A и B}$ – логические переменные, представляющие собой положительные сигналы от 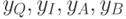соответственно.

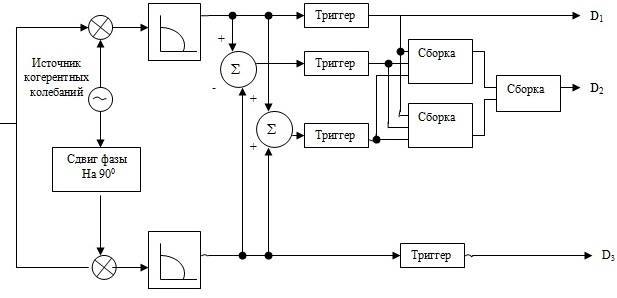
Другой метод детектирования сигналов с 8 ФМ, при котором не требуются дополнительные опорные колебания и ФД, следует из формул (4.2). Дополнительные измерения могут быть определены в виде:

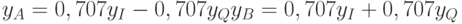$y_A=0,707y_I-0,707y_Q\\ y_B=0,707y_I+0,707y_Q\\$

( 4.5)

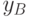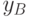Другими словами, величины y_A и y_B могут определяться в виде линейных комбинаций измерений фазы в квадратурных каналах y_A и y_B , не требуя дополнительных ФД. Соответствующие модулятор и демодулятор показаны на рис. 4.8 .

Рис. 4.8. Демодулятор, использующий всего два опорных колебания

Линейные комбинации (4.3) представляют вращение базисных векторов в квадратурных канала на угол $\frac{\pi}{4}$ . Изменяя угол вращения можно легко найти линейные комбинации в других случаях фазовой модуляции. Следовательно, все демодуляторы, в состав которых входят ФД, могут быть реализованы с помощью двух ФД и комбинаций, в которых вращение происходит на произвольный угол $\alpha$ ,имеют вид: