НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 16: Алгоритмически разрешимые проблемы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: свободно | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать программу

15.4. Проблема пустоты языка

Теорема 15.4.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, верно ли, что $L(G) = \varnothing$ .

Доказательство. Удалим из G все бесполезные символы, кроме начального символа (как в доказательстве теоремы 8.1.3). Если полученная грамматика содержит хотя бы одно правило, то $L(G) \neq \varnothing$ .

Упражнение 15.4.2. Является ли непустым язык, порождаемый грамматикой

$\begin{align*} S \; & {\to} \; a a C M , & K \; & {\to} \; b T , \\ S \; & {\to} \; a a a K F , & K \; & {\to} \; a T , \\ M \; & {\to} \; a M b , & T \; & {\to} \; b K a , \\ M \; & {\to} \; b M a , & T \; & {\to} \; a b ? \\ M \; & {\to} \; \varepsilon , \\ C \; & {\to} \; a C a , \\ C \; & {\to} \; b C b , \end{align*}$

15.5. Проблема бесконечности языка

Теорема 15.5.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, является ли бесконечным язык L(G).

Пример 15.5.2. Рассмотрим контекстно-свободную грамматику G из примера 8.1.4. Чтобы выяснить, является ли язык L(G) бесконечным, удалим сначала все бесполезные символы. Затем устраним все $\varepsilon$ -правила. Так как $W \overstar{\Rightarrow} Z$ и $Z \overstar{\Rightarrow} W$ , то можно всюду заменить W на Z. Получится грамматика

$\begin{align*} S \; & {\to} \; V Z , & Z \; & {\to} \; aab , \\ T \; & {\to} \; aa , & Z \; & {\to} \; b , \\ T \; & {\to} \; bb , \\ V \; & {\to} \; a T b , \\ V \; & {\to} \; b T a , \end{align*}$

эквивалентная исходной грамматике G. Очевидно, что эта грамматика не содержит "рекурсивных" нетерминальных символов. Следовательно, язык L(G) является конечным.

Упражнение 15.5.3. Является ли бесконечным язык, порождаемый грамматикой

$\begin{align*} S \; & {\to} \; a F , & S \; & {\to} \; a a C M , & C \; & {\to} \; a C a , \\ F \; & {\to} \; J , & S \; & {\to} \; a a a K F , & C \; & {\to} \; b C b , \\ F \; & {\to} \; a , & M \; & {\to} \; a M b , & K \; & {\to} \; b T , \\ J \; & {\to} \; F , & M \; & {\to} \; b M a , & K \; & {\to} \; a T , \\ J \; & {\to} \; b , & M \; & {\to} \; \varepsilon , & T \; & {\to} \; b K a , \\ & & & & T \; & {\to} \; a b ? \end{align*}$

15.6. Проблема эквивалентности конечных автоматов

Теорема 15.6.1. Существует алгоритм, позволяющий по произвольным двум праволинейным грамматикам G₁ и G₂ узнать, верно ли, что $L(G_1) \subseteq L(G_2)$ .

Теорема 15.6.2. Существует алгоритм, позволяющий по произвольным двум праволинейным грамматикам G₁ и G₂ узнать, верно ли, что L(G₁) = L(G₂).

Упражнение 15.6.3. Эквивалентны ли грамматика

$\begin{align*} S \; & {\to} \; aab S , \\ S \; & {\to} \; aaba \end{align*}$

и грамматика

$\begin{align*} S \; & {\to} \; a T , \\ U \; & {\to} \; ba T , \\ T \; & {\to} \; a U , \\ T \; & {\to} \; aba ? \end{align*}$

15.7*. Проблема эквивалентности детерминированных МП-автоматов

Теорема 15.7.1. Существует алгоритм, позволяющий по произвольным двум детерминированным МП-автоматам M₁ и M₂ узнать, верно ли, что L(M₁) = L(M₂).

Эту теорему доказал Жеро Сенизерг (Geraud Senizergues) в 1997 году. Упрощенное доказательство приводится в [Sti].

Упражнение 15.7.2. Эквивалентны ли два изображенных ниже МП-автомата над алфавитом $\{ a , b , \eos \}$ ?

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{a,\varepsilon:A} \rloop{0,-1} ^{b,AA:\varepsilon} \ar "1,2" ^{\boldsymbol{\$},\varepsilon:\varepsilon} & *=[o][F=]{2} } \qquad \objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{aa,\varepsilon:B} \rloop{0,-1} ^{b,B:\varepsilon} \ar "1,2" ^{\boldsymbol{\$},\varepsilon:\varepsilon} & *=[o][F=]{2} }$

Упражнение 15.7.3. Эквивалентны ли два изображенных ниже МП-автомата над алфавитом $\{ a , b , \eos \}$ ?

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{a,\varepsilon:A} \ar "1,2" ^{b,\varepsilon:\varepsilon} & *=[o][F-]{2} \rloop{0,1} ^{b,AA:\varepsilon} \ar "1,3" ^{\boldsymbol{\$},\varepsilon:\varepsilon} & *=[o][F=]{3} } \qquad \objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \rloop{0,1} ^{aa,\varepsilon:B} \ar "1,2" ^{b,\varepsilon:\varepsilon} & *=[o][F-]{2} \rloop{0,1} ^{b,B:\varepsilon} \ar "1,3" ^{\boldsymbol{\$},\varepsilon:\varepsilon} & *=[o][F=]{3} }$

15.8*. Классы P и NP

Определение 15.8.1. Пусть машина Тьюринга M допускает язык L. Говорят, что язык L распознается за полиномиальное время на машине M, если существует такой многочлен p, что любое слово 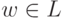$w \in L$ принимается машиной M не более чем за p(|w|) тактов.

Определение 15.8.2. Через P обозначается класс тех языков, которые распознаются за полиномиальное время на некоторой детерминированной машине Тьюринга.

Определение 15.8.3. Через NP обозначается класс тех формальных языков, которые распознаются за полиномиальное время на некоторой (в общем случае недетерминированной) машине Тьюринга.

Замечание 15.8.4. Очевидно, что $\mathrm{P} \subseteq \mathrm{NP}$ . Неизвестно, совпадают ли классы P и NP.

Теорема 15.8.5. Все языки из класса NP являются разрешимыми.

Определение 15.8.6. Всюду определенная функция f из 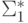$\Sigma_1^*$ в $\Sigma_2^*$ называется вычислимой за полиномиальное время, если ее вычисляет некоторая детерминированная машина Тьюринга M (если $\Sigma_1 \neq \Sigma_2$ , то данная функция f рассматривается как частичная функция из $(\Sigma_1 \cup \Sigma_2)^*$ в $(\Sigma_1 \cup \Sigma_2)^*$ ) и существует такой многочлен p, что для любого слова $w \in \Sigma_1^*$ машина M вычисляет значение f(w) не более чем за p(|w|) тактов.

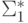Определение 15.8.7. Язык $L_1 \subseteq \Sigma_1^*$ полиномиально сводится (is polynomial time reducible) к языку $L_2 \subseteq \Sigma_2^*$ , если существует такая вычислимая за полиномиальное время всюду определенная функция f из $\Sigma_1^*$ в $\Sigma_2^*$ , что для любого слова $w \in \Sigma_1^*$ условие $f ( w ) \in L_2$ равносильно условию $w \in L_1$ .

Определение 15.8.8. Формальный язык L называется NP- сложным (NP-hard}, если каждый язык из класса NP полиномиально сводится к языку L.

Определение 15.8.9. Формальный язык называется NP- полным (NP-complete), если он принадлежит классу NP и является NP -сложным.

Определение 15.8.10. Алгоритмическая проблема, относящаяся к некоторой задаче распознавания, называется NP- полной, если множество кодов индивидуальных задач с ответом "да" является NP-полным языком.

Теорема 15.8.11 (теорема Кука-Левина). Проблема выполнимости булевых формул в конъюнктивной нормальной форме N- полна.

Доказательство можно найти, например, в [Сэв, с. 325-328] или [ГэрДжо, с. 57-63].

Упражнение 15.8.12. Существует ли такой язык $L \subseteq \Sigma^*$ из класса P, что язык $\Sigma^* \sminus L$ не принадлежит классу P?

Упражнение 15.8.13. Существуют ли такие языки L₁ и L₂ из класса P, что язык $L_1 \cup L_2$ не принадлежит классу P?

Упражнение 15.8.14. Существуют ли такие языки L₁ и L₂ из класса NP, что язык $L_1 \cup L_2$ не принадлежит классу NP?

Дальше >>

Математическая теория формальных языков

Математическая теория формальных языков