| Россия, Республика Хакасия, г. Абакан |
Нейросетевая модель целераспределения для вычислительной системы архитектуры data flow
Просеребрив на небе след,
Ракета вышла на ракету.
Мы этот миг сквозь толщи лет
Передадим как эстафету.
Г.В. Кисунько, Генеральный конструктор
первой в мире системы ПРО,
"Мы слышим первыми всегда"
Задача целераспределения
С начала 80-х годов прошлого века перспективные исследования в области вычислительной техники во многом определялись концепцией "японского вызова". В рамках этой концепции были обоснованы два положения:
- должны быть созданы нейросетевые методы вычислений часто решаемых оптимизационных задач высокой сложности;
- вычислительная система (ВС) должна объединять десятки тысяч микропроцессоров, взаимодействующих по технологии data flow.
Первое положение должно было обеспечить рост эквивалентной производительности ВС за счёт реализации более простых алгоритмов решения нейросетевых и нейроподобных задач.
Второе положение должно было обеспечить параллельное решение этих задач с минимальными накладными расходами в высокопараллельной ВС, способной, в том числе, воспроизводить структуру нейронной сети. В этом случае реальная производительность нейрокомпьютера эквивалентна той производительности, что требуется для решения конкретной задачи численными методами.
Одной из центральных задач, решаемых в начале боевого цикла системы обороны, является задача целераспределения, к оперативному решению которой предъявляются наиболее высокие требования [29]. В классической постановке это транспортная задача линейного программирования с рядом дополнительных условий и ограничений. Такая задача высокой сложности требует применения методов искусственного интеллекта.
Пусть территориально распределённая система обороны включает станции обнаружения и несколько стрельбовых комплексов, обладающих зонами поражения. Станции обнаружения с помощью своих вычислительных средств, используя, например, метод наименьших квадратов при обработке группы обнаруженных точек, формируют полиномы целей, как функции времени t, для расчёта их текущих координат и параметров движения. Обычно это – полиномы четвёртой степени вида
x = a01 + a11t + a21t2 + a31t3 + a41t4 y = a02 + a12t + a22t2 + a32t3 + a42t4 z = a03 + a13t + a23t2 + a33t3 + a43t4.
Представленные полиномы могут описывать центр групповой цели. По результатам дальнейших наблюдений эти полиномы уточняются.
Таким образом, данные полиномы описывают модель движущейся цели, пересекающей зоны поражения и в разной степени достижимой средствами перехвата стрельбовых комплексов с учётом их готовности.
Эффективность системы целераспределения характеризуется:
- минимальным предотвращённым ущербом;
- временем готовности стрельбового комплекса к выполнению новой задачи;
- временем подготовки пуска перехватчика с момента выдачи целеуказания при предпочтительности дальнего перехвата;
- коэффициентом загрузки стрельбового комплекса по групповой цели;
- параметрами взаимного пространственного расположения цели и перехватчика в момент выдачи главной команды и пр.
Известны попытки решения задачи целераспределения в статическом режиме для отражения единичной или групповой цели. Однако следует ориентироваться на динамический характер отражения многих целей массированного налёта в течение относительно длительных боевых действий, при которых необходимо учитывать ущерб, нанесённый прорвавшимися целями.
Тогда задача целераспределения превращается в трудно формализуемую логико-комбинаторную оптимизационную задачу, оперативное решение которой основано на переборе и анализе большого количества связок вида "если – то". Здесь и целесообразно использовать аппарат логических нейронных сетей, имитирующий ассоциативное мышление человека на основе накопленного опыта и обучения. Решение задачи, во многом воспроизводящее артиллерийские приёмы накопления опыта пристрелки и переноса огня, строится на основе экспертных оценок, на базе натурных экспериментов и результатов моделирования. По результатам таких исследований создаётся база знаний (БЗ), отображающая связи между возможными ситуациями и принимаемыми по ним решениями. При формировании этих связей (при обучении нейронной сети) учитываются требования эффективности решений. Ситуации задаются возбуждением рецепторов. Возбуждение нейронов, реализующих пороговую функцию активации, указывает на рекомендуемое назначение стрельбового комплекса. При не числовом характере вывода решение принимается по наиболее "возбудившемуся" нейрону, что и свойственно задаче целераспределения.
Наполнение базы знаний возможно по принципу очевидной целесообразности при оценке взаимного расположения объектов и возможных характеристик налёта. Сложные случаи требуют создания комплексной имитационной модели с применением средств анимации и компьютерной графики. Модель должна обеспечить возможность имитации различных сценариев действий противника для формирования различных вариантов налёта. Она должна отображать различные способы противодействия не только в поиске успешных, но и оптимальных в смысле предъявляемых выше требований. При этом модель должна адекватно воспроизводить физические законы движения управляемых объектов и целей. Задачей моделирования является покрытие факторного пространства отношениями вида "если – то" ("параметры удара – выбор средства отражения") для решения задачи целераспределения в рамках более общей задачи управления боевыми действиями.
Логическая нейронная сеть для решения задачи целераспределения
Пусть на основе моделирования построены М опорных траекторий, равномерно или с учётом опасных направлений покрывающих обороняемую территорию. Выбраны оптимальные варианты их "обслуживания" основными стрельбовыми комплексами (СК) и их дублёрами - на случай низкой готовности или выхода из строя основных средств.
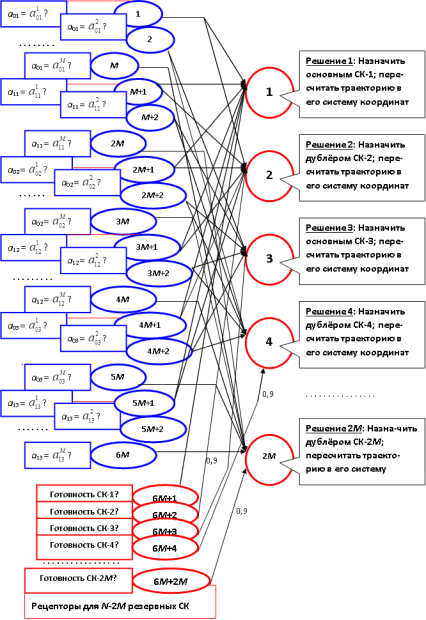
Составим примерную, легко развиваемую логическую нейронную сеть (рис. 14.1), позволяющую принять решение о назначении главного СК и его дублёра по значениям коэффициентов полиномов цели. Рассматривая возможности целераспределения на принципиальном уровне, допустим, что двух коэффициентов в уравнениях каждой координаты движения достаточно для представления о характере цели. То есть, по этим коэффициентам можно с достаточной точностью определить опорную траекторию, на которую в большой степени "похожа" анализируемая траектория, подлежащая "обслуживанию".
Кроме того, для лучшего понимания принципа назначения СК для поражения цели, на рис. 14.1 отражён ряд допущений.
- Предполагается, что значения коэффициентов a011, a012, ..., a01M по координате x для М опорных траекторий образуют возрастающую последовательность, и за каждым из них закрепляется рецептор. В действительности, этот порядок следования может быть нарушен. Если же для двух или более из М траекторий эти коэффициенты равны, то их значение представляет лишь один рецептор.
- Значения коэффициентов a111, a112, ..., a11M по координате x для всех опорных траекторий тоже образуют возрастающую последовательность отличных друг от друга значений. В ней повторяется тот же порядок представления М траекторий, что и в последовательности a011, ..., a01M. В действительности, возрастающая последовательность этих коэффициентов в общем случае отображает другой порядок представления траекторий, а одинаковые значения коэффициентов определяют другое количество рецепторов, закреплённых за вторым коэффициентом в уравнении по координате x.
- То же касается последовательности коэффициентов a021, a022, ..., a02M и последовательности a121, a122, ..., a12Mпо координате y, а также последовательности a031, a032, ..., a03M и последовательности a131, a132, ..., a13M по координате z. То есть, в общем случае коэффициенты одной опорной траектории оказываются независимо рассредоточены по возрастающим последовательностям, а общее количество рецепторов, закреплённых за значениями коэффициентов, лишь не превышает значение 6М. Однако связи с нейронами должны строго соответствовать принадлежности коэффициентов опорным траекториям, и из одного рецептора могут исходить более одной связи.
- Порядок нумерации стрельбовых комплексов и их оптимальное закрепление за опорными траекториями выбран так, чтобы, как и в пунктах 1 – 3, не в ущерб общности примера упростить индексацию, обеспечить наглядность и не запутать читателя нагромождением "правильных" абстрактных выкладок.
- Стрельбовых комплексов, с учётом назначения основных и дублёров, хватает для "обслуживания" М опорных траекторий и близких к ним реальных траекторий, т.е.
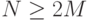 .
. -
В данном примере предполагается назначение основного и дублирующего СК для поражения одной цели. Однако в действительности на особенно опасном направлении может быть предусмотрено закрепление за опорными траекториями более одного СК – дублёра. Тогда по числу назначаемых средств поражения формируется и количество нейронов, закрепляемых за соответствующими опорными траекториями, а количество нейронов в логической нейронной сети может превышать значение 2М. Веса связей от дублирующих СК образуют убывающую последовательность, указывающую на приоритет дублёров. Так повышается вероятность назначения СК – дублёра только в том случае, когда основной СК и СК – дублёры более высокого приоритета обладают более низкой готовностью: временно заняты, исчерпали боекомплект или поражены. Функция активации нейрона имеет вид:
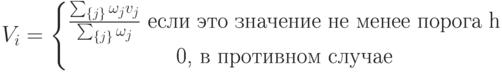
Здесь Vi – величина возбуждения i-го нейрона; {j}- множество связей i-го нейрона с рецепторами;
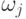 – вес j-й связи нейрона, vj – величина возбуждения j-го рецептора. Порог h выбирается экспериментально так, чтобы не "погасить" возбуждение нейронов, обусловленное СК-дублёрами при допустимом значении их готовности.
– вес j-й связи нейрона, vj – величина возбуждения j-го рецептора. Порог h выбирается экспериментально так, чтобы не "погасить" возбуждение нейронов, обусловленное СК-дублёрами при допустимом значении их готовности.
Обращение к логической нейронной сети для обработки каждой новой траектории производится отдельно, т.е. множество новых траекторий обрабатывается последовательно в цикле.
Если значение коэффициента а01 совпадает с одним из значений этого коэффициента, за которым закреплён рецептор, значение возбуждения этого рецептора полагается равным единице. Если значение а01 не совпадает ни с одним значением, за которым закреплён рецептор, находятся значения a01i и a01i+1, за которыми существуют закреплённые рецепторы и для которых выполняется условие: a01i< а01 < a01i+1. Значение возбуждения рецептора i полагается равным (a01i ( а01)/( a01i+1 ( a01i). Значение возбуждения рецептора i+1 дополняет найденное значение до единицы.
Аналогично "возбуждаются" один или два рецептора по значению коэффициента а11. Таким же образом "возбуждаются" рецепторы по уравнениям координат y и z.
Оценки готовности стрельбовых комплексов формируются на основе функционального контроля и системы управления боевыми действиями.
По сформированным значениям возбуждения рецепторов с помощью функции активации рассчитываются значения возбуждения всех нейронов. Максимально "возбудившийся" нейрон указывает на принимаемое решение. Оценка готовности используемого СК корректируется.
Если возбуждение ни одного нейрона не превысило порог, следует сделать вывод об ожидании освободившегося СК с высокой готовностью или об оперативном подключении других средств противодействия. Снижение порога не приведёт к какому-либо пересмотру действий по "обработке" данной цели.
Обратим внимание на важный элемент самообучения, реализуемый в ходе боевых действий. Траектории некоторых поражённых целей можно включать в опорные, тем самым развивая БЗ и её логическую нейронную сеть. (Это подобно тому, как в артиллерии команда "Стой! Записать..." в дальнейшем служит эффективному применению тактики переноса огня взамен трудоёмкой подготовки данных по новым целям.)
Наглядное изображение логической нейронной сети служит отражению смысла задачи, но не предоставляет формальных механизмов для компьютерной реализации. Метод вычислений основан на применении матрицы связей, соответствующей этой сети. Матрица связей и некоторая сопутствующая информация, ускоряющая расчёт, представлена в табл. 1.
При построении матрицы связей для каждого нейрона целесообразно формировать список индексов ненулевых весов связей с рецепторами. Это необходимо для ускоренного выполнения операции скалярного произведения разреженных (нулями) векторов, как основной трудоёмкой операции счёта значения функции активации. Как видно из рис. 14.1 и из табл. 14.1, в каждом скалярном произведении участвуют всего лишь семь элементов вектора веса каждого нейрона, какими бы большими ни были значения M и N.
Решение задачи целераспределения на ВС архитектуры data flow
В [14] содержится достаточно примеров программирования на ВС, управляемой потоком данных по технологии data flow. Однако каждая новая область применения порождает и новые рекомендации по системе команд.
Отметим, что каждый разработчик параллельных вычислительных систем утверждает, что он реализовал архитектуру data flow. Дело в том, что какими бы приёмами не осуществлялось распараллеливание вычислений, оно всегда основано на оценке готовности данных для программных модулей, процедур, инструкций и пр., распределяемых между исполнительными устройствами. Распределение, как правило, выполняется принудительно с помощью диспетчеров ОС или аппаратными средствами, приводящими к серьёзным накладным расходам производительности. Рассматриваемый здесь "чистый" принцип data flow отличается тем, что данные, являющиеся операндами в некоторой операции, по мере готовности поступают непосредственно в текст инструкции для выполнения этой операции. Операции, для которых в текст соответствующей инструкции поступили все необходимые данные, готовы к выполнению и могут быть "подхвачены" свободными ресурсами.
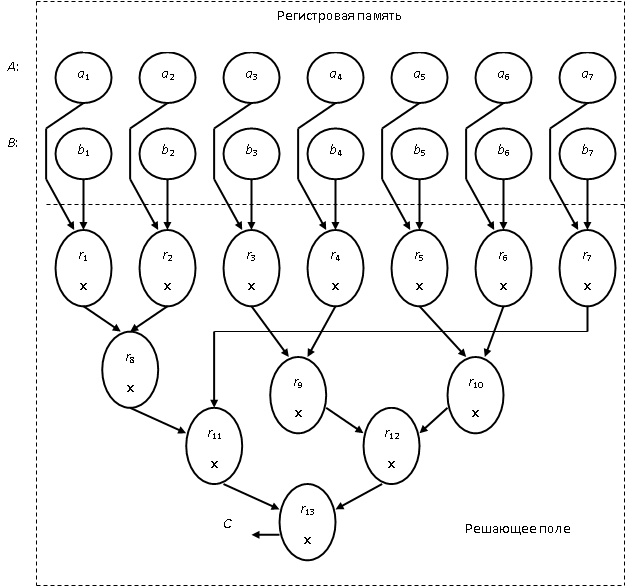
Составим план загрузки множества R = {r1, …, r2m-2} виртуальных вычислителей решающего поля ВС для счёта значения скалярного произведения двух векторов A = {a1, a2, …, am} и B = {b1, b2, …, bm} способом "пирамиды". Этот способ обеспечивает максимальные возможности распараллеливания таких связных процессов, как "свёртка массивов" или преобразование вида "вектор – скаляр". Для определённости положим m = 7 (рис. 14.2). В овалах указаны виртуальные адреса вычислителей и выполняемые ими операции.
Для счёта по данной схеме динамически формируются заявки к памяти, а также занимаются и частично заполняются инструкциями очередные свободные регистры в буферах физических вычислителей. Так создаётся схема коммутации вычислителей для выполнения данного алгоритма (рис. 14.3). Для краткости изложения предположим, что виртуальные адреса вычислителей на рис. 14.2 автоматически переведены в физические с сохранением их значения. Место временного хранения результата в регистре не показано.
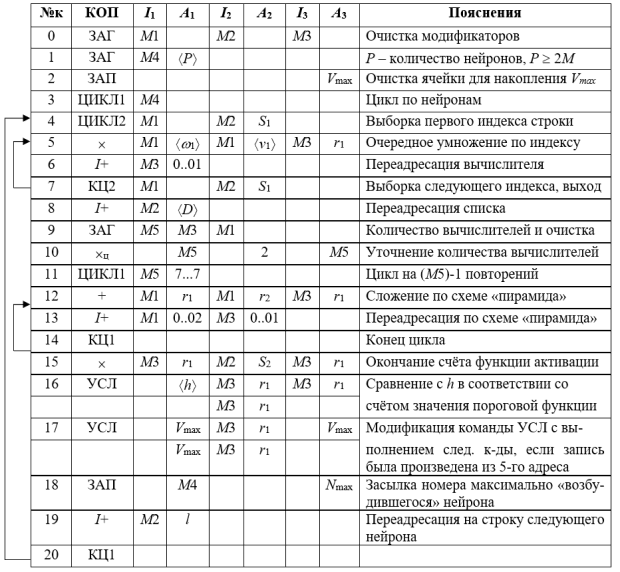
Представим программу нахождения решения о назначении СК для поражения цели с помощью логической нейронной сети. Фактически это программа стандартной процедуры НЕЙРОКОМПЬЮТЕР для ВС архитектуры data flow (рис. 14.4).
Поясним применение некоторых команд.
Команда ЦИКЛ1 выполняет простейший цикл типа арифметической прогрессии.
Команда ЦИКЛ2 соответствует конструкции, применяющей список индексов и даже выражений для их расчёта в полном описании ALGOL-60 Бэкуса – Бауэра [30]. В соответствии с этим обобщением предполагается непосредственно использовать список индексов элементов одного из двух векторов, отличных от нуля, для сокращения времени счёта их скалярного произведения. Первый индекс из списка выбирается при выполнении команды ЦИКЛ2. Остальные индексы формируются по команде КЦ2 (Конец Цикла 2). Предполагается, что список оканчивается либо пустым словом, либо специальным символом, выбор которого служит сигналом выхода из цикла. Это следует учитывать при формировании табл. 1, где размеры всех её позиций должны быть фиксированными в соответствии с целью применения. Это упрощает переадресацию. Более того, условия оперативного применения процедуры НЕЙРОКОМПЬЮТЕР требуют использования сверхоперативной, т.е. регистровой памяти.
Дважды применяемая команда УСЛ реализует конструкцию "if – then – else" [14] в двух модификациях. По команде 16 сравнение с порогом h позволяет окончательно сформировать значение пороговой функции активации, т.е. получить значение возбуждения нейрона: если  , с помощью пятого адреса подтверждается рассчитанное значение, в противном случае значение этой функции равно нулю.
, с помощью пятого адреса подтверждается рассчитанное значение, в противном случае значение этой функции равно нулю.
В команде 17 используется модификация, при которой также по третьему адресу направляются данные пятого адреса, если значение по первому адресу меньше значения по второму адресу. В противном случае по третьему адресу отправляются данные четвёртого адреса. Кроме того, если пересылка была произведена с пятого адреса, выполняется следующая команда 18. Такое выполнение команд 17 и 18 позволило зафиксировать новое значение максимально "возбудившегося" нейрона, а при выполнении следующей команды - получить значение параметра цикла, т. е. номер этого нейрона. Если пересылка была произведена с четвёртого адреса, следующая команда пропускается.
Краткие итоги
- На основе аппарата логических нейронных сетей построен "быстрый" алгоритм целераспределения. Логическая нейронная сеть интерпретирует базу знаний, в которой отражено соответствие между наиболее опасными опорными траекториями движения целей, "покрывающими" обороняемый район, и средствами их эффективного поражения.
- Назначение средств поражения для вновь обнаруженной траектории цели производится по принципу ассоциативных вычислений, по наибольшей похожести данной траектории на одну из опорных. Множество опорных траекторий и принимаемые по ним оптимальные решения выбираются на основе очевидных соображений по размещению объектов и средств, а также по результатам моделирования боевых действий.
- Траектории поражённых целей могут включаться в состав опорных, развивающих самообучающуюся базу знаний. В возможности самообучения заключается преимущество такого метода искусственного интеллекта, как аппарат логических нейронных сетей.
- Вычислительные системы, управляемые потоком данных (data flow) определяют высокий коэффициент полезной загрузки оборудования при решении задачи целераспределения нейросетевым методом.
- Представленная программа нейрокомпьютера на базе логической нейронной сети соответствует универсальной процедуре, которая может быть включена в состав общего программного обеспечения вычислительной системы архитектуры data flow.
Вопросы:
- В чём заключается метод опорных траекторий решения задачи целераспределения по нейросетевой технологии?
- Как проявляется возможность самообучения при применении нейросетевого метода целераспределения?
- Охарактеризуйте возможность достижения высокой эквивалентной производительности вычислительных средств при нейросетевом методе решения задачи целераспределения.
- В чём проявилась дальновидность разработчиков алгоритмического языка ALGOL-60 при счёте функции активации нейрона?
- Как, на ваш взгляд, с помощью трансформации и развития базы знаний может осуществляться эффективное сопротивление деградации системы в боевых условиях?