| Россия, Абакан, ХГУ им. Н. Ф. Катанова |
Развиваемая логическая нейронная сеть для распознавания объектов временного ряда по заданному набору признаков
Структурированная, не однослойная логическая нейронная сеть
Маша готова к компромиссу. Её представления об идеальном мужчине расширяются. В качестве желанного жениха она готова рассмотреть не менее шикарный вариант {блондин, рост от 180 до 190 см, нос "картошечкой", шляпа отсутствует}.
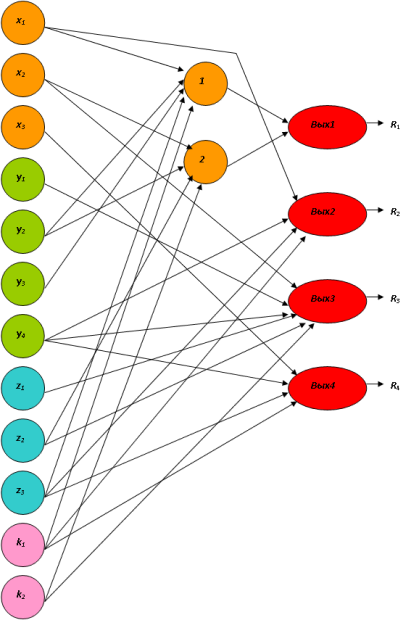
Казалось бы, достаточно дополнить нейронную сеть на рис. 9.1 связями, ведущими из рецепторов, соответствующих указанным параметрам, к нейрону Вых1, указывающему на решение R1. Однако это не так. При попытке ограничиться одним слоем, необходимо проверить, не поглотило ли множество рецепторов, участвующих в нахождении планируемого решения, некоторое его подмножество, инициирующее совсем другое решение. Следовательно, может случиться, что для некоторых ситуаций возможно неоднозначное решение.
В данном случае, при выбранном множестве решений, такая опасность пока отсутствует. Однако при расширении системы принятия решений, то есть при формировании новых решений по некоторым, пока не рассмотренным ситуациям, возможна неоднозначность рекомендуемых решений. Например, Маша скоро захочет сформировать новое решение R5 на основе логического выражения
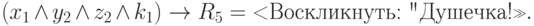
Легко видеть, что при непосредственном связывании рецепторов с нейронами выходного слоя в однослойной сети задание (единицами) указанной ситуации приведёт к активизации двух решений – R1 и R5.
Известны два способа ликвидации неоднозначности решений.
Первый способ заключается в строгом воспроизведении структуры нового логического выражения, определяющего решение R1:
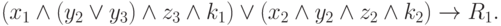 |
( 9.2) |
Наличие скобок указывает на структуризацию формируемой сети (рис. 9.2); она становится не однослойной.
В [7] показано, как, подбирая веса связей и значения порогов, добиваться высокой достоверности решений структурированной логической нейронной сети. Этот путь настолько сложен, что не рекомендуется на страницах данной книги. Тем более, что на основе фактов математической логики любая структурированная логическая нейронная сеть легко, ещё на уровне логического описания системы принятия решений, сводится к однослойной, не допускающей неоднозначных решений.
Преобразование структурированной нейросети в однослойную, допускающую неограниченное развитие
Второй способ ликвидации неоднозначности принимаемых решений называется размножением решений. Он заключается в том, что каждая конъюнкция в выражении вида (9.2) приводит к возбуждению одного нейрона выходного слоя. То есть, каждый нейрон, выполняющий роль конъюнктора, инициирует одно и то же решение, которое закреплено за разными нейронами.
В этом случае можно записать два логических выражения, обусловливающих решение R1: заданное первоначально и новое
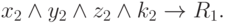
Появившаяся интерпретация того же решения вводит в искушение развития системы принятия решений. Например, первое вхождение R1 в описание системы может быть дополнено разъяснением:
R11 = <Сладко помечтать о возможном счастье с высоким брюнетом>.
Второе вхождение R1 может привести к аналогичному изменению:
R12 = <Сладко помечтать о возможном счастье с симпатичным блондином средней упитанности>.
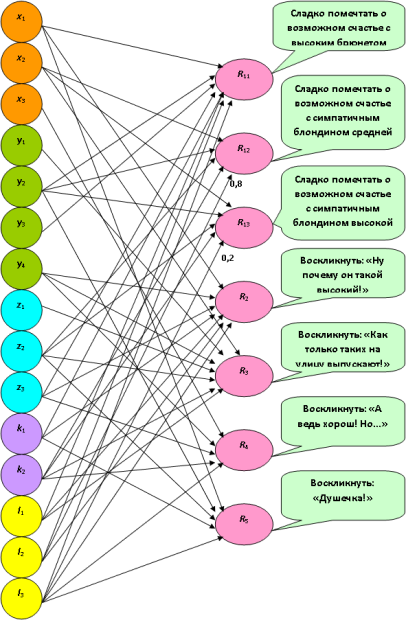
Таким образом, принимаемые решения в действительности отличаются одно от другого, а нейронная сеть остаётся однослойной (рис. 9.3). Это облегчает её обработку и исключает неоднозначность решений.
увеличить изображение
Рис. 9.3. Развитие однослойной логической нейронной сети с функцией активации (9.1)
И тут Машу впервые посещает мысль о действенности такого важного свойства – признака мужчины, как упитанность (на рис. 9.3 отражено решение R13 для признака высокой упитанности; веса, равные единице, не отмечены).
Создавая исчерпывающее множество событий, Маша полагает, что упитанность бывает низкой, средней и высокой.
Следовательно, необходимо рецепторный слой дополнить тремя рецепторами l1, l2 и l3. Влияние нового фактора на принятие решений неодинаково. Так, ситуация <высокий брюнет с длинным носом, да ещё и в шляпе>, приводящая к решению R11, подавляет фактор упитанности, исключает какую-либо зависимость от неё. Поэтому к решению R11 должны вести связи от всех рецепторов, ведающих упитанностью.
Ситуация, приводящая к решению R12, как говорилось ранее, напрямую учитывает фактор упитанности, но не так что уж полностью. Впервые введя веса и подумав, Маша решает учитывать среднюю упитанность с весом 0,8, а высокую – с весом 0,2. Решение R2 она не ставит в зависимость от упитанности. Поэтому, как и к решению R11, к решению R2 должны вести связи от рецепторов l1, l2 и l3. Решение R3 зависит от низкой упитанности с весом единица. Вес высокой упитанности при принятии решений R4 и R5 также принимается равным единице.
Введение в рассмотрение весов связей требует корректировки используемой функции активации (9.1).
Целесообразно выбрать следующую функцию активации на основе оценки средней величины сигнала, поступившей на i-й выход:

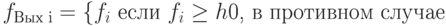 |
( 9.3) |
увеличить изображение
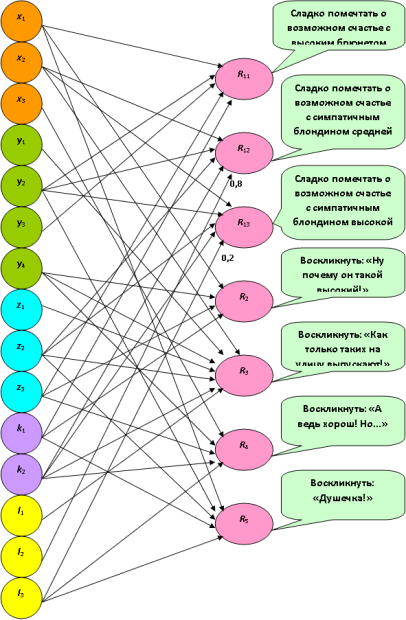
Рис. 9.4. Развитие однослойной логической нейронной сети с функцией активации (9.3)
Применение данной функции активации упрощает формирование связей между рецепторами и нейронами (рис. 9.4): связи устанавливаются лишь те, от которых решение действительно зависит. Например, решение R11 не зависит от упитанности – этих связей нет на рис. 9.4.