| Россия, Абакан, ХГУ им. Н. Ф. Катанова |
Силлогистика Аристотеля
Силлогизмы
Силлогизмы у Аристотеля – это выводы второго ранга, т.е. выводы, которые можно сделать на основании двух посылок. В этих посылках фигурируют три класса сущностей S, P и M. По многовековой традиции их называют меньший, больший и средний термин.
Каждая посылка и заключение представляют собой базовые высказывания силлогистики.
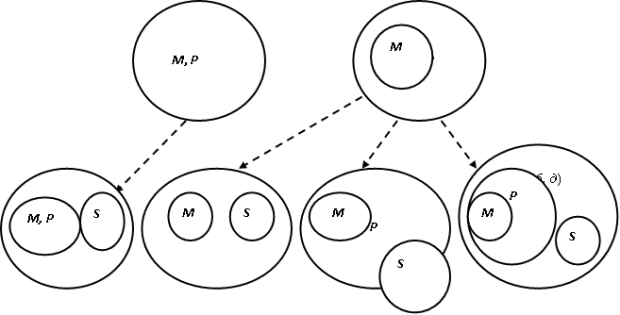
В соответствии с тем, как используются S, P и M в высказываниях, в силлогистике выделяют четыре фигуры (рис. 2.2), пронумерованные на рисунке.
Каков смысл этих фигур?
Возьмём первую фигуру. Для того чтобы породить с её помощью конкретные типы силлогизма (они называются модусами), надо выбрать из четырёх символов A, E, I, O по одному для первой и второй посылок и для заключения. Количество комбинаций расстановки четырёх символов по трём позициям равно 43 = 64. При четырёх фигурах это даёт 256 различных модусов. Проиллюстрируем несколько возможных модусов для первой фигуры.
Рассмотрим комбинацию AAA. Ей соответствует следующий модус силлогизма:
Всякий М есть Р
Всякий S есть М
_______________
Всякий S есть Р
Попробуем проверить правильность этого силлогизма. А именно, если его посылки истинные, то всегда ли будет истинным заключение? Для этого используем жергоновы отношения в табл.1. Первая посылка, как это следует из таблицы, даёт две возможности соотношений М и Р. Эти возможности показаны в верхнем ярусе на рис. 2.3. Поскольку вторая посылка тоже истинна, то на нижнем ярусе того же рисунка показаны области, в которых одновременно выполняются требования к истинности обеих посылок.
Таких возможных областей три, как это видно из рисунка. Для всех трёх областей между S и Р имеются жергоновы отношения такого типа, который обеспечивает истинность заключения силлогизма. Это значит, что при истинности его посылок результат вывода, т.е. переход к заключению, всегда возможен, и заключение будет истинным.
Рассмотрим другой пример, приняв модус первой фигуры EIO
Всякий М не есть Р
Всякий S есть М
_______________
Всякий S не есть Р.
Для первой посылки есть одна возможная область истинности, показанная на верхнем ярусе рис. 2.4. При добавлении второй посылки с учётом требований к её истинности можно получить четыре варианта, показанные на втором ярусе рисунка.
Все четыре полученные области являются областями истинности для базового высказывания, соответствующего заключению в этом силлогизме. Следовательно, истинность его посылок всегда обеспечивает истинность заключения.
Рассмотрим, наконец, ещё один пример, взяв модус AEE первой фигуры на рис. 2.2.
Всякий М есть Р
Всякий S не есть М
_______________
Всякий S не есть Р.
Соответствующая графическая интерпретация дана на рис. 2.5.
Для первой посылки возможны две области истинности в жергоновых отношениях, показанные на верхнем ярусе рисунка. Добавление второй посылки, показанное на нижнем ярусе рисунка, при первой возможности для первой посылки однозначно, а для второй возможности приводит к трём различным возможностям расположения трёх классов сущностей. А именно, два средних случая на нижнем ярусе приводят к ложности заключения. Следовательно, силлогизм АЕЕ не является правильным. Из истинности его посылок не всегда следует истинность его заключения. Вот пример такого ошибочного заключения:
Всякий железный брусок тонет в воде
Всякий кирпич не есть железный брусок
__________________________________
Всякий кирпич не тонет в воде.
Таким образом, имеются силлогизмы, которые всегда обеспечивают правильный вывод, т.е переход к истинному заключению при истинности двух посылок. А есть силлогизмы неправильные, не обеспечивающие такого заключения.
Закономерен вопрос: сколько силлогизмов из 256 возможных являются правильными? Ответ на него и есть ядро силлогистики. Перебирая все возможные модусы, можно обнаружить, что лишь 24 модуса являются правильными, а все остальные могут привести к ошибочному выводу.
Таким образом, правильные модусы образуют ядро теории дедуктивного вывода, в которой от правильных посылок всегда гарантируется переход к правильному заключению. Но, как стало ясно в последующих столетиях, Аристотель создал ядро дедуктивной теории, которое позволило расширить его, сохраняя все основные исходные положения.
На этом мы остановимся в изучении силлогистики Аристотеля. Дело в том, что последующие её расширения (прежде всего, введение операции отрицания) привели к современному состоянию теории "Математическая логика". Как было показано в Лекции 1, именно на её базе (и на базе элементов теории вероятностей) построена математическая логика событий, легшая в основу логических нейронных сетей – средств реализации многих задач искусственного интеллекта.
Краткие итоги
- В силлогистике Аристотеля впервые и до настоящего времени утвердилось понятие о трёх типах рассуждений: дедуктивных, индуктивных и от частного к частному.
- Индуктивные или правдоподобные рассуждения способны породить лишь гипотезу, нуждающуюся в подтверждении практикой, опытом.
- Введение понятий сущностей и их классов, а также кванторов, поднимает силлогистику с уровня исчисления высказываний на уровень исчисления предикатов.
- Базовые высказывания – предикаты образуют восемь схем, определяющих систему аксиом силлогистики.
- Теоретико-множественный подход позволяет наглядно представить характер взаимоотношений между сущностями классов – построить жергоновые отношения.
- На основе кванторов и классов сущностей сформулированы четыре закона (A, E, I, O) силлогистики, породившие кванторы общности и существования современной математической логики.
- Исследование истинности основных типов силлогизмов исчерпывает требования практического применения силлогистики сегодня.
Вопросы
- Каковы исходные положения силлогистики Аристотеля?
- Каковы три типа рассуждений?
- Почему для практических применений высказывания в силлогистике неотделимы от сущностей и их классов?
- Используя кванторы, приведите восемь схем базовых высказываний в силлогистике.
- Объясните понятие жергоновых отношений.
- Объясните три закона силлогистики.
- Приведите четыре фигуры силлогизмов Аристотеля и схемы доказательства их истинности. Сколько силлогизмов являются "правильными"?