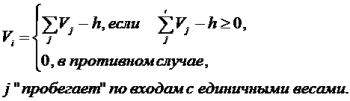Математическая логика событий и логические нейронные сети

Минимизация длины логической цепочки в системе принятия решений

Замена логических операций операцией суммирования при счёте передаточной функции приводит к актуальности однократного учёта всех входящих переменных, т.е. к единственности вхождения переменных в каждое логическое выражение, составляющее описание системы принятия решений. Выше с целью обеспечения такого единственного вхождения переменной был использован приём "размножения" решения R₆.

При разработке электронных схем исследуется понятие "длина логической цепочки" - под ней подразумевается максимальное количество электронных элементов, которое должен преодолеть сигнал на входе схемы, пройдя последовательное тактируемое преобразование, чтобы на выходе схемы сформировался сигнал. От этой длины, определяющей время переходного процесса, зависит быстродействие схемы. Поэтому актуальной задачей является минимизация максимальной длины логической цепочки при возможности параллельного выполнения всех таких цепочек (что характерно для прохождения электрического сигнала по схеме).

Очевидно, что в схеме на рис. 1.4 максимальная длина логической цепочки равна двум.

Применим ко всем выражениям (1.5), каждое из которых является или может быть преобразовано в дизъюнкцию конъюнкций, приём "размножения" решений. Теперь (рис. 1.9) схема состоит из цепочек единичной длины. Каждый входной сигнал подвергается обработке только конъюнктором. Так как электронная схема полностью определяет конструкцию системы принятия решений на основе достоверности событий, то можно преобразовать полученную электронную схему в однослойную схему СПР, показанную на том же рисунке.

увеличить изображение
Рис. 1.9. Преобразование электронной схемы с единичной длиной логической цепочки в однослойную систему принятия решений

Таким образом, доказано следующее утверждение:

Любая СПР, сформированная на основе логического описания булевыми функциями, способом "размножения" решений преобразуется в однослойную СПР на основе достоверности событий.

Преимуществом таких СПР является то, что они представляют собой таблицы с ассоциативной выборкой по принципу наибольшей похожести.

Конечно, можно за каждым решением закреплять один выход СПР, на котором объединить общее решение, полученное по разным путям, в виде текста. При корректно заданных исходных данных – на основе правил использования исчерпывающих множеств событий – СПР будет "работать" правильно, выдавая адекватные ответы. Тогда рекомендация "Прими решение R" будет выдана, но информация о пути, приведшему к этому решению, будет утрачена.

При составлении "электронной" схемы такое объединение производится с помощью операции дизъюнкции, что приводит к длине логической цепочки, равной двум. Но ведь если, формируя структуру СПР, строго следовать порядку построения "электронная схема 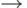система принятия решений", то и СПР будет иметь максимальную логическую цепочку с длиной, равной 2.

Таким образом, "размножение" решений – операция, целесообразность которой свойственна СПР, что делает её построение отличающимся, развивающим "схемотехнический" подход. "Электронные" схемы целесообразно использовать на начальном этапе исследования логического описания СПР, а далее, оттолкнувшись от них, перейти к более совершенной однослойной структуре.

"Размножение" решений имеет важное достоинство. Оно позволяет установить причину, дополнительно объяснить принимаемое решение, учесть в тексте аргументацию. Это означает, что текст решения может быть дополнен указанием причины принятия именно такого решения.

Например, получив информацию о необходимости заказа велосипеда в отделе спортинвентаря, бабушка может воспользоваться и важным объяснением: "… потому что сейчас, скорее всего, весна, а Вы, вероятно, только что сытно позавтракали" (рис.1.10).

увеличить изображение
Рис. 1.10. Бабушка

Таким образом, построен алгоритм параллельных (бесформульных!) вычислений сложных логических конструкций в области действительных переменных, предназначенный для реализации высокого быстродействия в системах управления и принятия решений. Более того, сведение СПР к однослойной нейросети приводит к применению лишь тех передаточных функций (элементов N₁ на рис. 1.6 и 1.9), которые имитируют конъюнкторы. Это служит повышению достоверности оценок, стандартизации и адекватности природным процессам.

увеличить изображение
Рис. 1.11. Логическая нейронная сеть БАБУШКА.

От логических операций совершён переход к их некоторым суррогатам на основе передаточной функции. Операционной основой этой функции является сложение взвешенных сигналов на входе. Логические переменные оказались заменёнными действительными – достоверностью высказываний.

Изображая передаточную функцию буквой N, и уже назвав её однажды функцией активации, мы подразумеваем нейрон, нейроподобный элемент - исполнитель этой функции активации, способный, подобно кирпичику, участвовать в образовании сложных сетевых структур. Теперь мы можем на рисунке 1.9 заменить квадратики кружочками, подразумевая нейроны, как это отображено на рис. 1.11.

При этом функции активации являются простейшими (монотонно возрастающими по каждому сигналу на входе), и выбираться "на вкус". Как говорилось выше, операция сложения взвешенных сигналов на входе является основой такой функции. Практически всегда весами являются "нули" или "единицы".

В данном примере можно рекомендовать функцию активации:

Значение h = 1 гарантирует выполнение условия 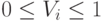. Это упрощает применение формируемого на выходном слое сигнала для входа в следующую нейронную сеть длинной логической цепочки.

Выбор и обоснование функции активации нейрона

Требования к функции активации:

1. Эти функции в области преодоления порога должны быть монотонно возрастающими по каждому сигналу на входе нейрона;
2. Сигнал возбуждения при его прохождении по сети не должен угасать;
3. Сигналы возбуждения на выходном слое должны быть четко различимы по величине для различных эталонных ситуаций;

4. Должен быть примерно равным диапазон изменения величин возбуждения нейронов выходного слоя, закрепленных за разными решениями.

   Приведём ряд функций активации, тривиальных по выполнению и используемых в данной книге:

   1. 
   2. 
   3. 
   4. 

   5. Достаточно универсальной функцией активации является функция возбуждения нейрона по усреднённому значению сигналов на его входах (дендритах). Это усреднённое значение сигналов и принимается, как величина возбуждения нейрона.

      ,

      Если все веса , то функция активации находится:

      

Не следует забывать, что нейронную сеть, реализующую СПР, необходимо рассматривать как одно звено в цепочке логического вывода, вырабатывающее информацию для последующих звеньев цепочки. Это позволяет строить сложные, многоуровневые СПР, как цепочки логических выводов, реализующие дедуктивное и даже индуктивное мышление.

Конкретно это означает, что величины возбуждения нейронов выходного слоя должны, как и величины возбуждения рецепторов, принадлежать диапазону [0, 1], моделируя всё ту же достоверность выводов.

В однослойных нейронных сетях, где хороша каждая из перечисленных функций активации, предлагается использовать функцию активации 5. Здесь особенно актуально то, что прообразом нейрона выходного слоя является конъюнктор. Легко видеть, что величина возбуждения каждого нейрона сети удовлетворяет указанному диапазону.

Функция активации 4 применима в задачах логического вывода, а также в системах диагностики, т.к. близка к воспроизведению булевой переменной.

Можно придумать и другие функции активации, удовлетворяющие приведённым выше требованиям.

Краткие итоги

1. Корректно составленная система принятия решений оперирует исчерпывающими множествами событий.
2. Несколько исчерпывающих множеств событий, являющихся предметом исследования при построении системы принятия решений, образуют факторное пространство событий.
3. Взаимосвязь событий различных исчерпывающих множеств целесообразно отображать деревом логических возможностей. Оно позволяет выделять множества совместных событий, находить вероятности их наступления, строить факторные подпространства событий.
4. Дерево логических возможностей позволяет корректно строить логические функции в основе системы принятия решений.
5. Реализация логических функций по технологии "электронных" схем позволяет построить систему принятия решений, оперирующую с булевыми переменными. Применение исчерпывающих множеств событий исключает необходимость операции НЕ.
6. Переход от булевых переменных к действительным – к достоверностям высказываний о наступлении событий – возможен с помощью нечёткой логики, основанной на приближённом исполнении схем И и ИЛИ на нейроподобных элементах.
7. Дальнейший переход к нейронным сетям при сохранении правильной работы системы принятия решений также оказывается результативным, так как следует Природе.
8. Структура нейронной сети может быть значительно упрощена по известным в математической логике и в схемотехнике методам сокращения максимальной длины логической цепочки. Так формируются однослойные нейронные сети.

Вопросы:

1. Что представляет собой исчерпывающее множество событий?
2. Что представляет собой факторное пространство событий и как его структуризация с помощью дерева логических возможностей помогает корректно сформировать логическое описание системы принятия решений?
3. Как формируется полное и непротиворечивое логическое описание системы принятия решений?
4. Как логическое описание преобразуется в форму, предполагающую однослойную нейронную сеть?
5. Как осуществляется переход к нечётким данным – к достоверностям высказываний о наступлении событий?
6. Как на основе "схемотехнического" подхода производится обоснование однослойных логических нейронных сетей, реализующих системы принятия решений?