|
Курс Технология блокчейн и Биткоин Лекция 1. Раздел: Сравнение процедуры традиционной банковской онлайн транзакции и транзакции в сети Биткоин. Сравнение не убедительное. В приведенном примере оплаты за ритейл-услугу (покупка чашки кофе) получается, что подтверждения транзакции в сети Биткойн нужно ждать час, а при использовании традиционного POS-терминала подтверждение мгновенное (а при использовании банком системы мгновенных платежей, средства будут зачислены на счет продавца в другой банк почти мгновенно). При этом, покупатель при блок-чейне оплачивает комиссии сам, т.е. сумма на ценике и сумма перевода разные, а при использовании POS-терминала сколько на ценике, столько и списывается. Чем в приведенном примере для участников транзакции использование блок-чейн отличается от использования простых электронных кошельков? Не могу отделаться от ощущения, что блк-чейн - очередная "мода", позвляющая ИТшникам полчать финансирование.
|
Строение блокчейна
Общие понятия
Цель: Сформировать общее представление о блокчейне как цепочке блоков, уточнить основные термины и понятия.
В рамках этого курса мы намеренно смешиваем два термина: "распределенный реестр данных" и "блокчейн", следуя традиции, сформированной нашими законодателями, не делающими между ними различий. На самом деле это не синонимы. Эти понятия состоят в родо-видовых отношениях. Технология блокчейна является разновидностью распределенных реестров. При этом далеко не все распределенные реестры (DLT, distributed ledger technology) являются блокчейнами.
Обе эти технологии объединяет децентрализация и достижение консенсуса между нодами. Основное отличие носит структурный характер. Для блокчейна характерно хранение данных в виде последовательности криптографически защищенных блоков. Такая структура используется как надежная (математически гарантировано) основа для безопасного достижения достоверного консенсуса. Далеко не все распределенные реестры устроены аналогичным образом. Кроме этого, блокчейн не допускает удаления (и даже изменения) транзакций. Разрешены только операции добавления новых записей, сгруппированных в блоки. Т.е., фактически блокчейн можно интерпретировать как постоянно растущий реестр записей.
Закончим это небольшое уточнение определением DLT. Далее продолжим использовать термины распределенный реестр и блокчейн, не вдаваясь в детали и не делая между ними различия.

Distributed ledger technology — это технология хранения данных, для которой характерны: совместное использование и синхронизация цифровых данных в соответствии с алгоритмом консенсуса; географическое распределение идентичных копий во многих точках мира; отсутствие единого центра управления.
Определим блокчейн (распределенный реестр) как динамическую структуру в формате упорядоченного обратно связанного списка блоков – групп записей (транзакций). Физически блокчейн может храниться в виде набора переменных и их значений (плоский файл) или в простейшей базе данных, поскольку не требуется применять сложные модели представления данных. Например, эталонный клиент Bitcoin Core для хранения метаданных блокчейна использует базу данных LevelDB (высокопроизводительная, не реляционная, NoSQL СУБД, фиксирующая данные в формате ассоциированных пар: ключ=значение) производства компании Google.
Блоки связаны с помощью обратных ссылок, т.е., каждый блок (кроме генезисного) ссылается на предыдущий блок в общей цепочке. Для визуализации блокчейна часто используют образ вертикальной стопки лежащих друг на друге блоков. Именно этот образ способствовал появлению таких терминов как "высота блока", обозначающего расстояние до блока генезиса и "вершина блокчейна", указывающего на последний добавленный блок.
Для идентификации блока в блокчейне используется его хеш, полученный с помощью криптографического алгоритма SHA-256. Причем рассчитывается дайджест хеша только на основе заголовка блока. Для реализации механизма связей внутри блокчейна в заголовок каждого блока включено значение хеша родительского блока. Эта цепочка хешей тянется от текущего блока к блоку генезиса, включая все промежуточные блоки блокчейна без исключения.
Каждый блок может иметь ровно одного родителя. Однако в сети Биткоин иногда возникают ситуации, когда у некоторого блока оказывается больше одного потомка. Сразу скажем, что это явление временное и требующее исправления. Речь идет о разветвлениях блокчейна, имеющих место, когда несколько майнеров одновременно формируют валидные блоки. Эти блоки включаются в альтернативные ветви блокчейна. И разница между такими реализациями блокчейна может составить даже несколько блоков. Однако, в итоге достаточно быстро действительной будет признана только одна – та которая в текущий момент является более длинной.
Представим, что мы злоумышленники и попробуем атаковать какой-нибудь блок, расположенный где-нибудь внутри цепочки – не на вершине блокчейна. Даже не будем касаться вопроса как этот модифицированный блокчейн удастся навязать остальным полным нодам, у которых имеется своя, правильная версия реестра. Давайте просто оценим насколько сложно будет обмануть хотя бы самих себя. Любые изменения содержимого блока (транзакций) неизбежно отразятся на его заголовке (изменится содержимое поля "Корень дерева Меркла", в котором хранится хеш всех транзакций блока). Модифицированный заголовок даст нам новый хеш. Но ведь в оригинальной версии блокчейна исходное значение хеша было записано в поле "Хеш предыдущего блока" в потомке атакованного нами блока. И с учетом этого значения был рассчитан хеш блока-потомка. Значит придется пересчитывать так же хеш потомка. И так далее вверх по цепочке, вплоть до блока, находящегося на вершине блокчейна. Мы уже знаем, что ввиду особых требования к формату, вычисление "правильного" хеша блока – задача архисложная. А пересчитать сразу несколько блоков и успеть это сделать до того, как майнерами будет подготовлен новый блок (иначе придется пересчитывать и его), практически невозможно. Каждый добавленный блок повышает гарантии целостности сохраненных ранее данных. Это основа безопасности платформы Биткоин.
Проблема ветвления блокчейна ставит под сомнение (весьма условно) последние 5-6 блоков. Однако, информация, расположенная в блокчейне ниже, гарантированно является достоверной.
Анатомия блока
Цель: Досконально рассмотреть строение отдельного блока блокчейна платформы Биткоин.
Блок выполняет не только функции контейнера для хранения транзакций. Во многом именно на эти небольшие структуры данных ложится задача достижения консенсуса в платежной системе Биткоин.

Блок в криптовалютной платформе – это статическая структура данных специального вида, содержащая информацию о транзакциях, сделках и контрактах, проводимых в рамках платежной системы, защищенных криптографическими методами.
Блок платформы Биткоин состоит из заголовка с метаданными и множества транзакций, на которые приходится львиная доля размера блока (Таблица 5.1). Заголовок блока имеет стандартный размер 80 байт. Транзакция в среднем "весит" порядка 250 байт. Обычно в среднестатистическом блоке содержится не менее 500 транзакций. Нехитрая арифметика позволяет получить соотношение размеров заголовка блока и его остальной части.
| Размер | Поле | Описание |
|---|---|---|
| 4 байта | Magic number | Магическое число. Значение всегда равно 0xD9B4BEF9 (в шестнадцатеричном формате) |
| 4 байта | Размер блока (blocksize) | Меняется в зависимости от числа вошедших в блок транзакций. Максимальный размер блока в сети Биткоин = 1МБ (соглассно классического протокола Биткоин). Сеть не примет блок размером больше максимального предела. |
| 80 байт | Заголовок блока (blockheader) | Включает шесть полей |
| От 1 до 9 байт | Счетчик транзакций (transaction counter) | Число транзакций в данном блоке |
| Без ограничения | Транзакции (transactions) | Множество транзакций, включенных в данный блок |
Самое интересное хранится в заголовке блока (Таблица 5.2, Рисунок 5.1). Его содержимое можно условно разделить на три части в соответствии с решаемыми задачами.
| Размер | Поле | Описание |
|---|---|---|
| 4 байта | Версия (Version) | Номер версии для отслеживания обновлений программного обеспечения клиентов или протоколов сети Биткоин |
| 32 байта | Хеш предыдущего блока (Prev_block) | Ссылка на предыдущий (родительский) блок в блокчейне. Хранит значение хеш-функции, рассчитанного на основе заголовка блока-родителя |
| 32 байта | Корень дерева Меркла (Merkle_root) | Хеш корня дерева Меркла транзакций данного блока |
| 4 байта | Временная метка (Timestamp) | Приблизительные дата и время создания данного блока (в формате ОС Unix) |
| 4 байта | Целевая сложность (Bits) | Целевое значение (вычислительная сложность) алгоритма доказательства работы для данного блока (target). Элемент самоорганизации сети Биткоин, автоматически регулирующий сложность задачи майнинга. |
| 4 байта | Варьируемое случайное число (Nonce) | Значение этого счетчика используется в алгоритме доказательства работы. Изменяя Nonce, майнер стремится получить хеш заголовка заданной формы (меньше чем target) |
Прежде всего отметим поле "Хеш предыдущего блока". Этот элемент отвечает за связи между блоками, благодаря ему, собственно, мы можем говорить о цепочках блоков, т.е., блокчейне.
Второй комплекс метаданных включает целевую сложность, временную метку и случайный счетчик (Nonce). Два последних поля заполняются конкретным майнером, построившим очередной валидный блок. Все это – важнейшие компоненты алгоритма достижения консенсуса путем доказательства работы (Proof-of-work).

Доказательство выполнения работы относится к хешу заголовка блока. Блок считается действительным тогда и только тогда, когда его хеш меньше чем текущее целевое значение. Любой новый блок связан с предыдущим блоком и усиливает предыдущие доказательства выполнения работы, формируя цепочку блоков, называемую блокчейном. Когда блокчейн сформирован, он подтверждает все включенные в него транзакции и обеспечивает целостность и безопасность сети.
Третья часть отвечает за безопасность системы и совместно с другими элементами заголовка обеспечивает такое важнейшее свойство блокчейна как неизменяемость данных. Достигается все с помощью поля, содержащего хеш корня дерева Меркла – индикатора целостности и средства быстрой проверки транзакций данного блока.
Отметим, что после имплементации обновления SegWit реальный лимит размера блока повышен до 4 МБ, а лимит данных транзакций вырос почти до 2 МБ.
Идентификация блоков
Цель: Сформировать представление способах идентификации блоков в блокчейне платформы Биткоин.
Блоки в блокчейне принято адресовать (идентифицировать) по двум параметрам: хеш заголовка блока и высота блока. В качестве основного идентификатора используется специальный криптографический дайджест, полученный путем двойного применения к заголовку блока хеш-функции SHA-256 = (SHA-256(SHA-256(заголовок блока))).
Хотя полученный в результате криптографического преобразования 32-байтный дайджест практически всегда называют хешем блока (кстати, в этой книге также использовался именно этот термин), аргументом первого алгоритма SHA-256 является исключительно заголовок блока.
В качестве примера приведем хеш блока генезиса:
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
Уникальные значения хеша однозначно идентифицируют каждый блок и легко могут быть вычислены любым узлом сети Биткоин.
Любопытным свойством реализации системы является тот факт, что хеш блока не хранится в его структуре ни во время трансляции по сети, ни до, ни после включения в блокчейн. Каждый раз, когда какому-то узлу нужен хэш блока, узел его вычисляет. В некоторых системах хеши блоков могут содержаться в отдельной таблице базы данных, как часть метаданных блока, в целях облегчения операций индексации и поиска, а также ускорения процедуры считывания блоков из постоянной памяти.
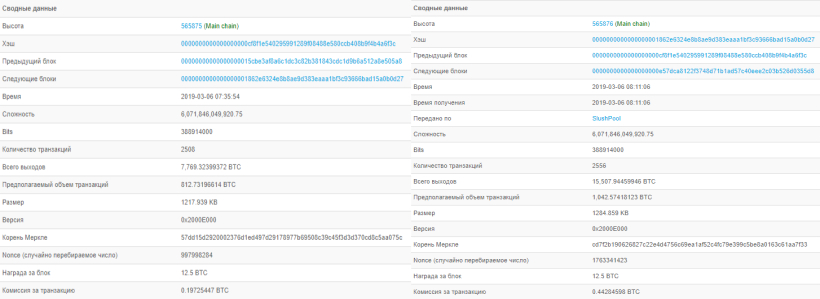
С высотой блока в качестве идентификатора дело одновременно обстоит и проще, и сложнее одновременно. С одной стороны, схема индексирования очень простая. Блок генезиса имеет высоту равную 0. Каждый последующий блок, включенный в блокчейн, имеет высоту на 1 больше предыдущего блока. Высота блока, созданного 6 марта 2019 года, примерно в 11 чсасов (по московскому времени), равнялась 565 875, то есть с момента создания блока генезиса в январе 2009 года в блокчейн платформы Биткоин было включено 565 875 блоков. Кстати следующего 565 876 блока пришлось ждать дольше 30 минут – явный сбой майнинговой составляющей сети. Зато следующий бок - 565 877 – прорвался в блокчейн, явно опережая график, всего через 6 минут. Карточки двух этих соседних блоков представлены на рисунке ниже.
увеличить изображение
Рис. 5.2. Краткая статика блоков блокчейна Биткоина с высотами 565 875 и 565 876
Некоторая проблема процесса идетификации с помощью высоты блока заключается в том, что, строго говоря, значения этого измерителя не являются гарантированно уникальными (в отличие от хеша блока). Несмотря на то, что каждый конкретный блок всегда имеет однозначно определенную, постоянную высоту, обратное утверждение ложно. В случае ветвления основной цепочки блоков появляются два (или даже более) блоков с одинаковой высотой и конкурирующих за единственную позицию в блокчейне. Разумеется, явление это временное (в итоге победит блок, оказавшийся в более длинной цепочке), но вполне возможное в сети Биткоин.
Высота блока также не хранится в заголовке блока и рассчитывается каждым узлом сети динамически. Некоторые приложения, работающие поверх Биткоина, для ускорения поиска хранят высоту блоков в индексированной таблице специализированной базы метаданных.
Блок Генезиса
Цель: Рассмотреть строение блока генезиса платформы Биткоин.
Первый блок в любом блокчейне называют блоком генезиса. Блок генезиса платформы Биткоин был создан в 2009 году. Его высота рана 0.

Блок генезиса - это цифровой объект, представляющий собой самый первый блок в блокчейне. Этот блок является прапредком любого другого блока в цепочке. Блок генезиса обязательно имеется у каждой криптовалюты и практически всегда реализуются программным способом. Блок генезиса должен быть проработан особенно тщательно, поскольку он лишен фундаментальной основы безопасности блокчейна, заключающейся в связанности с предыдущими блоками.
Блок генезиса реализован программным образом (статически) в клиентском программном обеспечении и в принципе не может быть модифицирован. В этот блок включена единственная транзакция, отправившая первые 50 BTC на один из адресов Сатоши Накамото - 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa. Используя любой обозреватель блокчейна сети Биткоин, можно посмотреть как содержимое блока генезиса, так и некоторые дополнительные сведения:
{
"hash" : "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f",
"confirmations" : 308321,
"size" : 285,
"height" : 0,
"version" : 1,
"merkleroot" : "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",
"tx" : [
"4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b"
],
"time" : 1231006505,
"nonce" : 2083236893,
"bits" : "1d00ffff",
"difficulty" : 1.00000000,
"nextblockhash" : "00000000839a8e6886ab5951d76f411475428afc90947ee320161bbf18eb6048"
}
В блоке генезиса сети Биткоин заключено некое скрытое сообщение. Вход coinbase-транзакции содержит следующий текст – копию заголовка передовицы газеты Таймс от 3 января 2009 года: "Таймс 03/Янв/2009 Министр экономики на грани второго раунда спасения банков". Эксперты предполагают, что, с одной стороны, это сообщение могло послужить доказательством временной вехи появления самого блока и, собственно, блокчейна сети Биткоин. С другой, это вполне может быть лозунгом создания независимой монетарной системы. Напомню, что в 2008-2009 гг. всю мировую финансовую систему потряс мощнейший финансовый кризис.
Добавление блоков в блокчейн полной нодой
Цель: Подробно рассмотреть процедуру добавления полной нодой новых блоков в блокчейн сети Биткоин, наглядно проиллюстрировать связь между блоками.
Полные ноды содержат актуальную локальную копию блокчейна, начиная с блока генезиса (реализованного непосредственно в программном обеспечении ноды). Реестр, хранимый нодой, перманентно обновляется и растет синхронно с появлением новых блоков. Получив очередной валидный блок из сети нода верифицирует его, а затем добавляет в локальную версию блокчейна. Связывание основной цепочки и нового блока осуществляется посредством мостика в виде "хеша предыдущего блока".
Пусть по состоянию на утро 7 марта 2019 года полная нода обладала локальным блокчейном, состоящим из 566 017 блоков. Блок, находящийся на вершине, имеет высоту = 566 016 (не забываем про блок генезиса с выстотой = 0) и хеш заголовка = 0000000000000000001ce2dbd9013f0fbe8a2c44574efe56712e6f9a4205c69e.
Через некоторое время (напомню, что заявленный в 10 минут интервал - это всего лишь усредненный на достаточно большом числе блоков показатель) нода из сети получает новый блок, высота которого после включения в блокчейн станет равной 566 017.
Для ноды его структура будет интерпретирована следующим образом:
{
"size" : 223292,
"version" : 0x20000000,
"previousblockhash" :
"0000000000000000001ce2dbd9013f0fbe8a2c44574efe56712e6f9a4205c69e",
"merkleroot" :
"e7dfbbad942b4f2dfa78363950f47a618f0e56e976c4fb107b35bfe56d322c7d",
"time" : 1551948693,
"difficulty" : 388914000,
"nonce" : 1864204227,
"tx" : [
"257e7777fb8bc68421eb2c7b699dbab234831600e7352f0d9e6522c7cf3f6c77",
… хеши еще 378 транзакций
"05cfd77f6ae6aa83674cc99e4d75a1458c165b7ab84725eda41d018a09177734"
]
}
Нода проверяет значение поля "хеш предыдущего блока" (т.е., родителя). В нашем случае он совпадает с хешем самого верхнего блока в локальном блокчейне. Т.е., новый блок является дочерним по отношению к нему и должен быть добавлен на вершину локального блокчейна, тем самым расширив его ровно на 1. Текущая высота блокчейна становится равной 566 017. На рисунке 5.3 демонстрируется механизм связи между блоками в блокчейне сети Биткоин на примере реальных данных.
Отметим, что для удобства восприятия на рисунке 5.3 структура блока несколько расширена. Добавлено сразу несколько полей (высота, хеш, следующие блоки, сложность, награда за блок, комиссионные), которые в реальном блокчейне отсутствуют.
Дерево Меркла
Цель: Сформировать представление о задачах, выполняемых с помощью дерева Меркла, подробно рассмотреть процедуру его построения.
Как известно, узлы в сети Блокчейн трудятся: а) анонимно и б) в условиях всеобщего недоверия. Информация о сделках хранится в транзакциях, собранных в блоки. Поскольку доверие отсутствует, следовательно, все данные должны пройти процедуру верификации. Для проверки всех блоков потребуются огромные вычислительные ресурсы. Во многих случаях этого можно избежать и помочь нам в этом способны деревья Меркла.

Деревом Меркла (хеш-деревом) называют двоичное дерево, в качестве листьев которого выступают хеши транзакций, а внутренними вершинами являются хеши, полученные на основе объединения информации дочерних узлов (обычно складываются значения пары дочерних узлов). Фактически, дерево Меркла является однонаправленной хеш-функцией. В некоторых источниках дерево Меркла может задаваться аббревиатурой TTH (Tiger Tree Hashing). Такая концепция впервые была запатентована Ральфом Мерклом в 1979 году, а соответствующая структура данных названа в его честь.
Транзакции внутри блока записаны в виде списка строк в шестнадцатеричном формате (raw transaction format). Каждая транзакция хешируется для получения идентификатора транзакции (txid). Как мы уже знаем, неизменяемость и связность блокчейна обеспечивается посредством учета в каждом блоке хеша предыдущего блока, значение которого рассчитывается только на основе его заголовка, исключая транзакции. Каким же образом учитывается в этой схеме обеспечения доверия фактическая информация о сделках (транзакции)? С помощью специальной структуры, вбирающей в себя данные всех включенных в конкретный блок записей (транзакций). Этой структурой является дерево Меркла. Корень этого дерева (хеш-дайджест) как одно из полей заголовка неизбежно отразится на хеше блока. Тем самым в этом основном идентификаторе блокчейна будет учтена вся история и условия сделок, зафиксированных в каждом конкретном блоке.
Деревья Меркла весьма популярны в среде IT-разработчиков. В файловых системах хеш-деревья применяются для выявления ошибок в потоках информации, распределенные СУБД с их помощью синхронизируют записи. Технология блокчейн использует деревья Меркла для организации упрощенной процедуры верификации транзакций.
В первую очередь это касается SPV-клиентов. Они не хранят блокчейн целиком и запрашивают все необходимые данные о транзакциях у полных нод. Поскольку речь идет о сетевом трафике, чрезвычайно важно использовать алгоритмы, минимизирующие объем передаваемых данных. Для этой цели используется доказательство Меркла, состоящее из транзакции, корня дерева и ветви, включающей хеши от запрашиваемой транзакции до корня. Агрегируя запрошенные хеши и сравнивая их с корнем, клиент может убедиться, что транзакция находится на заявленном месте в блоке, или наоборот опровергнуть это утверждение.

Доказательством Меркла называют криптографическое обоснование принадлежности определенных данных некоторому криптографическому обязательству в формате дерева Меркла или какого-либо его варианта. С помощью этого алгоритма возможно компактно доказать факт хранения определенных данных в составе заданного блока блокчейна. Одновременно с этим доказательство не может раскрыть иную информацию о состоянии транзакций блока. Используя доказательство Меркла, клиент может проверить подлинность транзакции без необходимости установления контактов с несколькими полными нодами и не реплицируя все транзакции блокчейна.
Благодаря такому механизму возможно обработать сколь угодно большие объемы информации. При этом нагрузка на сеть значительно снизится, поскольку передаваться будет только ограниченный набор необходимых хешей. Например, размер блока с 2048 транзакциями составит более 500 Кбайт. Размер доказательства Меркла (по-другому: размер пути) в аналогичном случае не превысит 352 байт.
А теперь научимся строить дерево Меркла самостоятельно. Построим обобщенный цифровой отпечаток всей совокупности транзакций блока. Сама процедура формирования дерева Меркла носит рекурсивный характер. Для каждой пары узлов дерева мы находим комбинированный хеш и так продолжаем до тех пор, пока не доберемся до самого верхнего узла, хеш которого называется корнем Меркла (Merkle root).
В качестве криптографического хеша в деревьях Меркла сети Биткоин используется достаточно традиционная комбинация для этой платформы – двойная функция SHA-256, т.е., SHA-256(SHA-256(конкатенация содержимого пары дочерних узлов для внутренней вершины или транзакция для конечной вершины)).
Построение дерева Меркла
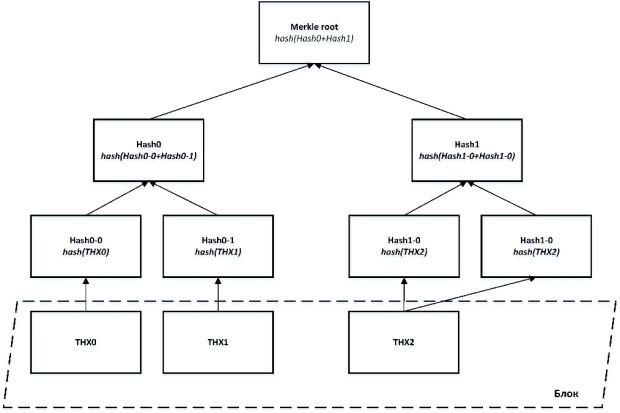
Заполнение вершин дерева начинается снизу – с листьев (см. Рисунок 5.4).
Сначала вычисляются хеши транзакций, сгруппированных в блоке Hash 0-i=hash(THX i)= SHA-256(SHA-256(THX i)). Вычисленные значения вписываются в листья дерева Меркле. Значения вершин более высоких уровней рассчитываются на основе хешей двух дочерних узлов: Hash j=hash(Hash j-0+Hash j-1)= SHA-256(SHA-256(Hash j-0+Hash j-1)). Например, для того чтобы построить родительскую вершину Hash0, два 32-байтных хеша дочерних узлов Hash 0-0 и Hash 0-1 объединяются (используется операция конкатенации) в единую 64-байтную строку. Полученная строка дважды хешируется Hash 0=hash(Hash 0-0+Hash 0-1)=SHA-256(SHA-256(Hash 0-0+Hash 0-1)) и результат записывается в соответствующий узел. Процедура повторяется до тех пор, пока не будет рассчитано значение верхнего узла – Merkle root. Таким образом, корень дерева Меркла инкапсулирует в себе данные всех транзакций блока.
Дерево Меркла является бинарным, поэтому должно содержать четное количество листьев. Если в блоке собрано нечетное число транзакций, то хеш последней транзакции просто дублируется, как это изображено на рисунке 5.4. В результате мы получаем, так называемое, сбалансированное дерево.
Поиск доказательства
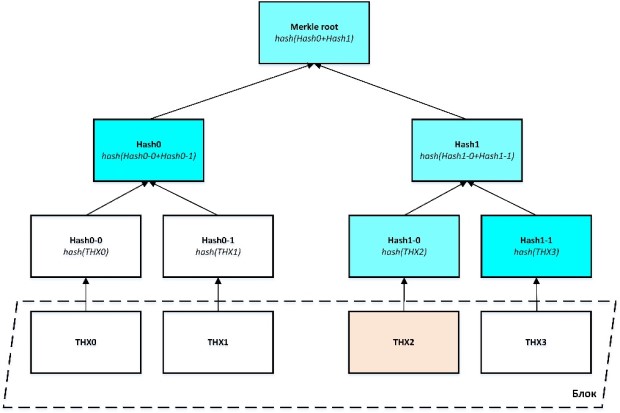
Применение деревьев Меркла позволяет доказать принадлежность определенного значения (транзакции) некоторому множеству (блоку) самым экономичным образом. В случае с платформой Биткоин мы крайне заинтересованы в том, чтобы проверка действительности транзакции ограничивалась пересчетом лишь относительно небольшого числа хешей, не затрагивая остальные. Процесс поиска доказательства Меркла иллюстрируется рисунком 5.5.
Предположим, что требуется проверить транзакцию THX 2. Для доказательства ее присутствия в блоке потребуются: корневой хеш, хеш верифицируемой транзакции, а также хеши узлов, составляющий, так называемый, путь Меркла (аутентификационный путь). В нашем примере путь Меркла включает вершины: Hash 1-1; Hash 1 и Hash 0.
Доказательство будет получено (т.е., проверка пройдет успешно), если
Merkle root = hash(Hash 0 + hash(hash(THX 2) + Hash 1-1)) = SHA-256(SHA-256(Hash 0+ SHA-256(SHA-256(SHA-256(SHA-256(THX 2)) + Hash 1-1)))).
Для нашего примера с четырьмя транзакциями применение доказательства Меркла конечно не является эффективным. Но если вспомнить о том, что число транзакций, входящих в реальный блок, может превышать 2 000 (для SegWit-формата), ситуация кардинально меняется. Эффективность применения деревьев Меркла становится очевидной, когда обрабатывается большое число объектов. В общем случае сложность алгоритма доказательства Меркла оценивается как O(K)=log2(N) действий, где K - высота дерева или длина пути Меркла, а N - это количество транзакций. Т.е., для поиска доказательства вхождения конкретной транзакции в определенный блок, содержащий N транзакций, ноде требуется вычислить примерно log2(N) 32-байтных хешей. Таблица 5.3 демонстрирует эффективность деревьев Меркла для доказательства присутствия транзакции в блоке.
| Количество транзакций | Приблизительный размер блока | Длина пути Меркле (в хешах) | Размер пути Меркла (в байтах) |
|---|---|---|---|
| 16 | 4 096 | 4 | 128 |
| 512 | 13 1072 | 9 | 288 |
| 2 048 | 524 288 | 11 | 352 |
| 65 535 | 16 777 216 | 16 | 512 |
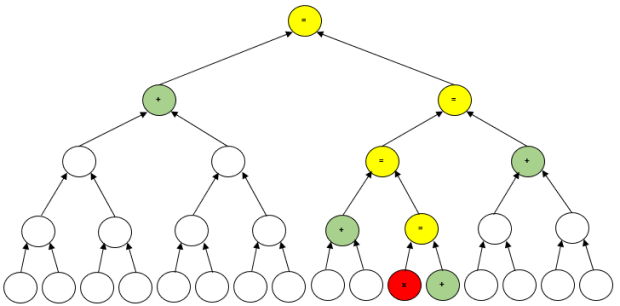
На рисунке 5.6 приведен еще один пример использования дерева Меркла, но только уже для 16 транзакций. Чтобы убедиться в принадлежности транзакции Х заданному множеству, мы должны вычислить путь Меркла длиной всего лишь четыре 32-байтовых хеша (всего 128 байт). Аутентификационный путь включает 4 вершины, отмеченных символом +. Для получения доказательства остается вычислить 4 дополнительных парных хеша (соответствующие вершины на рисунке 5.6 отмечены символом =) и сравнить полученное в итоге значение корня дерева Меркла с заявленным.
Используя технологию доказательства Меркле, SPV-узел может загружать в целях проверки только заголовки блоков (всего 80 байт на каждый блок) и тем не менее быть в состоянии подтвердить или опровергнуть факт включения транзакции в блок. Для этого достаточно запросить данные относительно короткого пути Меркла у любой полной ноды. Большая часть блокчейна при этом передаваться не будет. Для запроса легкими клиентами данных, позволяющих получить доказательство Меркла, в платформе предусмотрено сообщение merkleblock, содержащее заголовок блока, а также путь Меркла, связывающий заданную транзакцию с корнем дерева Меркла в блоке.
Двоичные деревья Меркла отлично справляются с задачей проверки последовательности элементов, поэтому они применяются для верификации транзакций SPV-кошельками. При этом функционал легких клиентов принципиально ограничивается. Например, невозможно узнать баланс средств по заданному адресу. Полный набор функций реализуется в системах, основанных на использования всего блокчейна.
Для преодоления ограничений традиционных алгоритмов постоянно разрабатываются новые. Например, во второй по уровню капитализации криптовалюте Ethereum используется, так называемое, префиксное дерево Меркла, концептуально основанное на ассоциативном массиве с ключами.
В отличие от бинарного дерева Меркла, ключ, идентифицирующий конкретную вершину, является "динамическим". Его значение зависит от местоположения на дереве и формируется в результате конкатенации символов, присвоенных ребрам графа, проходящим от корня до заданной вершины.
В платформе Ethereum заголовок блока включает сразу три префиксных дерева Меркла: для транзакций; информации об их выполнении и состоянии. В результате легкие клиенты получили возможность оперировать гораздо большим объемом данных. В частности, они самостоятельно могут ответить на вопросы типа: "Есть ли транзакция в указанном блоке?"; "Каков баланс счета?" и "В какое состояние перейдет система после выполнения данной транзакции?".
Краткие итоги
Для блокчейна характерно хранение данных в виде последовательности криптографически защищенных блоков. Такая структура используется как надежная (гарантировано математически) основа для безопасного достижения достоверного консенсуса. Определим блокчейн как динамическую структуру в формате упорядоченного обратно связанного списка блоков – групп записей (транзакций). Блоки связаны с помощью обратных ссылок, т.е., каждый блок (кроме генезисного) ссылается на предыдущий блок в общей цепочке. Для идентификации блока в процессе формирования ссылок используется его хеш, полученный с помощью криптографического алгоритма SHA-256.
Блок в криптовалютной платформе – это статическая структура данных специального вида, содержащая информацию о транзакциях, сделках и контрактах, проводимых в рамках платежной системы, защищенных криптографическими методами. Блок платформы Биткоин состоит из заголовка с метаданными и множества транзакций. Блок считается действительным тогда и только тогда, когда его хеш меньше чем текущее целевое значение. Любой новый блок связан с предыдущим блоком и усиливает предыдущие доказательства выполнения работы, формируя блокчейн. Когда блокчейн сформирован, он подтверждает все включенные в него транзакции и обеспечивает целостность и безопасность сети.
Блоки в блокчейне принято адресовать (идентифицировать) по двум параметрам: хеш заголовка блока и высота блока. В качестве основного идентификатора используется специальный криптографический дайджест, полученный путем двойного применения к заголовку блока хеш-функции SHA-256 - (SHA-256(SHA-256(заголовок блока))).
Блок генезиса - это цифровой объект, представляющий собой самый первый блок в блокчейне. Этот блок является прапредком любого другого блока в цепочке. Блок генезиса обязательно имеется у каждой криптовалюты и практически всегда реализуются программным способом.
Деревом Меркла называют двоичное дерево, в качестве листьев которого выступают хеши транзакций, а внутренними вершинами являются хеши, полученные на основе объединения информации дочерних узлов (обычно складываются значения пары дочерних узлов). Фактически, дерево Меркла является однонаправленной хеш-функцией. Доказательством Меркла называют криптографическое обоснование принадлежности определенных данных некоторому криптографическому обязательству в формате дерева Меркла или какого-либо его варианта. С помощью этого алгоритма возможно компактно доказать факт хранения определенных данных в составе заданного блока блокчейна.