Методы кластерного анализа. Итеративные методы.
При большом количестве наблюдений иерархические методы кластерного анализа не пригодны. В таких случаях используют неиерархические методы, основанные на разделении, которые представляют собой итеративные методы дробления исходной совокупности. В процессе деления новые кластеры формируются до тех пор, пока не будет выполнено правило остановки.
Такая неиерархическая кластеризация состоит в разделении набора данных на определенное количество отдельных кластеров. Существует два подхода. Первый заключается в определении границ кластеров как наиболее плотных участков в многомерном пространстве исходных данных, т.е. определение кластера там, где имеется большое "сгущение точек". Второй подход заключается в минимизации меры различия объектов
Алгоритм k-средних (k-means)
Наиболее распространен среди неиерархических методов алгоритм k-средних, также называемый быстрым кластерным анализом. Полное описание алгоритма можно найти в работе Хартигана и Вонга (Hartigan and Wong, 1978). В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для возможности использования этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров.
Алгоритм k-средних строит k кластеров, расположенных на возможно больших расстояниях друг от друга. Основной тип задач, которые решает алгоритм k-средних, - наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Выбор числа k может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции.
Общая идея алгоритма: заданное фиксированное число k кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга.
Описание алгоритма
- Первоначальное распределение объектов по кластерам.
Выбирается число k, и на первом шаге эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр.
Выбор начальных центроидов может осуществляться следующим образом:
- выбор k-наблюдений для максимизации начального расстояния;
- случайный выбор k-наблюдений;
- выбор первых k-наблюдений.
В результате каждый объект назначен определенному кластеру.
- Итеративный процесс.
Вычисляются центры кластеров, которыми затем и далее считаются покоординатные средние кластеров. Объекты опять перераспределяются.
Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий:
- кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации;
- число итераций равно максимальному числу итераций.
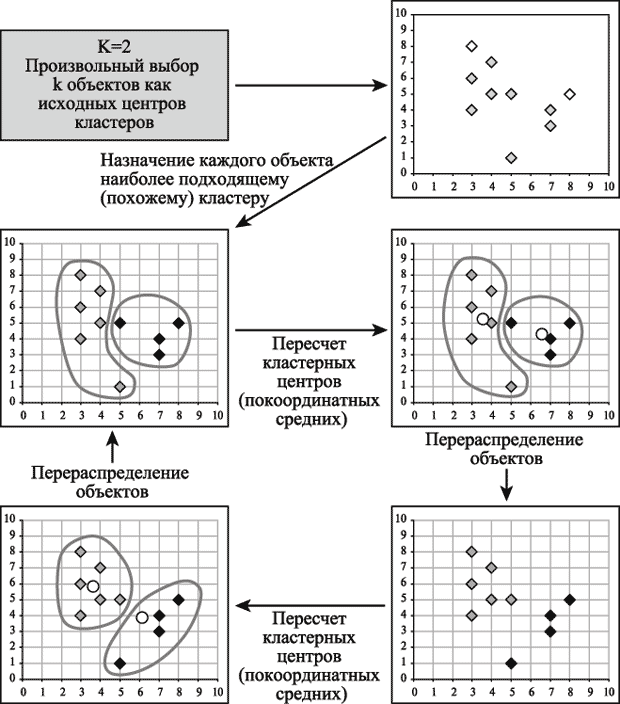
На рис. 14.1 приведен пример работы алгоритма k-средних для k, равного двум.
Выбор числа кластеров является сложным вопросом. Если нет предположений относительно этого числа, рекомендуют создать 2 кластера, затем 3, 4, 5 и т.д., сравнивая полученные результаты.
Проверка качества кластеризации
После получений результатов кластерного анализа методом k-средних следует проверить правильность кластеризации (т.е. оценить, насколько кластеры отличаются друг от друга). Для этого рассчитываются средние значения для каждого кластера. При хорошей кластеризации должны быть получены сильно отличающиеся средние для всех измерений или хотя бы большей их части.
Достоинства алгоритма k-средних:
- простота использования;
- быстрота использования;
- понятность и прозрачность алгоритма.
Недостатки алгоритма k-средних:
- алгоритм слишком чувствителен к выбросам, которые могут искажать среднее. Возможным решением этой проблемы является использование модификации алгоритма - алгоритм k-медианы;
- алгоритм может медленно работать на больших базах данных. Возможным решением данной проблемы является использование выборки данных.