Системы счисления. Перевод чисел из одной системы счисления в другую

Выбор системы счисления

Основными определяющими факторами в данном вопросе являются

• степень сложности выполнения арифметических операций в выбранной системе счисления,
• объем оборудования, необходимый для представления чисел в данной системе счисления, и
• условия реализации (создания) оборудования для представления цифр.

Если принять, что каждый разряд числа представлен не одним элементом с p устойчивыми состояниями, a p элементами, каждый из которых имеет одно устойчивое состояние, то показатель экономичности укажет условное количество оборудования, которое необходимо затратить на представление чисел в этой системе.

Допустим, что имеется n разрядов для изображения числа в р-ичной системе счисления. В этом случае максимальное число М будет отвечать выражению:

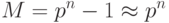( 6.2)

Наряду с величиной М, являющейся мерой максимального количества информации, которое может быть представлено в п разрядах, оценим число элементов N, необходимое для изображения числа М:

( 6.3)

Равенство (6.2) справедливо при условии, что для изображения каждого из допустимых в некотором разряде символов (цифр) требуется один элемент.

Определим N как непрерывную функцию от р и М. Из равенства (6.2) следует, что

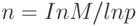
Подставляя это выражение в (6.3), получаем

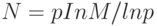
Используя полученную зависимость, можно найти основание системы счисления, при которой требуется минимум оборудования. Так, определив производную

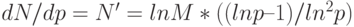
и приравняв ее к нулю, получим экстремум при р = е.

Характер экстремума соответствует минимуму, так как при р = е

N''>0

Таким образом, система при р = е требует минимума оборудования.

Но e = 2, 718… , т. е. не целое число. Поэтому на практике целесообразно использовать системы с основаниями р = 3 или р = 2. Эти системы, согласно приведенной оценке, практически равноценны, так как отношение

N₂/N₃ = (2 ln3) / (3 ln2)≈1,056

Подобное сравнение десятичной и двоичной систем показывает, что десятичная система примерно в полтора раза менее экономична двоичной:

N₁₀/N₂ = (10 ln2) / (2 ln10) ≈ 1,505