|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Проблемы устойчивости эконометрических процедур
Устойчивость по отношению к горизонту планирования
Продолжим начатое выше обсуждение влияние горизонта планирования на принимаемые решения. Отметим, что во многих реальных ситуациях продолжительность инвестиционного проекта не полностью определена либо горизонт планирования инвестора не охватывает всю продолжительность реализации проекта до этапа утилизации. В таких случаях важно изучить влияние горизонта планирования на принимаемые решения.
Рассмотрим условный пример. Предположим, я являюсь владельцем завода. Если горизонт моего планирования - 1 месяц, то наибольший денежный доход я получу, продав предприятие (включая здания, сырье, технологическое оборудование, землю, на котором стоит предприятие - если, конечно, я имею право ее продать). Если же планирую на год, то я сначала понесу затраты, закупив сырье и оплатив труд рабочих, и только затем, продав продукцию, получу прибыль. Если я планирую на 10 лет, то пойду на крупные затраты, закупив лицензии и новое оборудование, с целью увеличения дохода в дальнейшие годы. При планировании на 30 лет имеет смысл вложить средства в создание и развитие собственного научно-исследовательского центра, и т.д.
Подчеркнем - реальные инвестиции (в основные фонды - в здания, оборудование, в конструкторские разработки и т.д.), которые окупятся в следующие годы, в текущем году ухудшат многие финансово-хозяйственные показатели работы предприятия, сократят его прибыль, уменьшат показатели рентабельности, в итоги акционеры получат - в данном году - меньше.
Таким образом, популярное утверждение "фирма работает ради максимизации прибыли" или "цель фирмы - максимизация прибыли" не имеет точного смысла. За какой период максимизировать прибыль - за месяц, год, 10 или 30 лет? От горизонта планирования зависят принимаемые решения. Понимая это, ряд западных экономистов отказываются рассматривать фирмы как инструменты для извлечения прибыли, предпочитают смотреть на них как на квазиживые существа, старающиеся обеспечить продолжение своего существования и дальнейшее развитие. Соответственно с этим стратегический менеджмент исходит из понятий "миссия фирмы", "стратегические цели" (например, стратегическая цель может иметь вид: "повысить долю рынка, контрлируемую фирмой"), которые невозможно непосредственно выразить в денежных единицах (подробнее об этом см., например, учебное пособие [2]).
Прежде чем обсуждать непосредственно влияние горизонта планирования на принимаемые менеджером решения, рассмотрим классификацию используемых при принятии решепний оптимизационных моделей.
Характеризация моделей с дисконтированием. Пусть для простоты изложения время принимает дискретные значения. Тогда развитие экономической ситуации описывается последовательностью 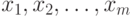 где переменные
где переменные 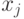 лежат в некотором пространстве
лежат в некотором пространстве 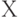 , возможно, достаточно сложной природы. Надо отметитть также, что положение в следующий момент не может быть прооизвольным, оно связано с положением в предыдущий момент. Проще всего принять, что существует некоторое множество К такое, что
, возможно, достаточно сложной природы. Надо отметитть также, что положение в следующий момент не может быть прооизвольным, оно связано с положением в предыдущий момент. Проще всего принять, что существует некоторое множество К такое, что 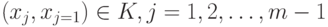 Результат экономической деятельности за
Результат экономической деятельности за  -ый период описывается величиной
-ый период описывается величиной 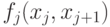 Зависимость не только от начального и конечного положения, но и от номера периода объясняется тем, что через номер периода осуществляется связь с общей экономической ситуацией. Желая максимизировать суммарные результаты экономической деятельности, приходим к постановке стандартной задаче динамического программирования:
Зависимость не только от начального и конечного положения, но и от номера периода объясняется тем, что через номер периода осуществляется связь с общей экономической ситуацией. Желая максимизировать суммарные результаты экономической деятельности, приходим к постановке стандартной задаче динамического программирования:
 |
( 1) |
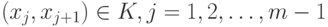
Таким образом, необходимо выбрать план 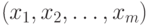 , удовлетворяющий приведенным ограничениям, на котором достигает максимума функционал
, удовлетворяющий приведенным ограничениям, на котором достигает максимума функционал 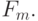 Естественно, предполагается, что множество возможных переходов К таково, что область определения функционала Fm не пуста. ПРи обычных математических предположениях максимум достигается.
Естественно, предполагается, что множество возможных переходов К таково, что область определения функционала Fm не пуста. ПРи обычных математических предположениях максимум достигается.
Как известно, задача (1) часто возникает во многих прикладных экономических и эконометрических областях, в макроэкономике, в логистике (управлении запасами) (см., например, монографию [1]).
Широко предлагаются, исследуются и применяются модели, приводящи5 к следующему частному случаю задачи (1):
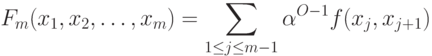 |
( 2) |

Это - модели с дисконтированием (как известно,  - дисконт-фактор). Естественно попытаться выяснить, какими "внутренними" свойствами выделяются задачи типа (2) из всех задач типа (1). В частности, почему такой большой популярностью пользуется характеристика инвестиционного проекта NPV ( Net Present Value - чистая текущая стоимость), относящаяся к характеристикам дисконтированного типа.
- дисконт-фактор). Естественно попытаться выяснить, какими "внутренними" свойствами выделяются задачи типа (2) из всех задач типа (1). В частности, почему такой большой популярностью пользуется характеристика инвестиционного проекта NPV ( Net Present Value - чистая текущая стоимость), относящаяся к характеристикам дисконтированного типа.
Представляет интерес изучение и сравнение между собой планов возможного экономического поведения на  шагов
шагов 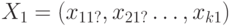 и
и 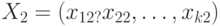 . (Естественно, предполагаем, что все пары соседних элементов входят в множество К.) Естественно сравнение проводить с помощью описывающих результаты экономической деятельности функций, участвующих в задачах (1) и (2). Именно, будем говорить, что план Х1 лучше плана Х2 при реализации с момента i, если
. (Естественно, предполагаем, что все пары соседних элементов входят в множество К.) Естественно сравнение проводить с помощью описывающих результаты экономической деятельности функций, участвующих в задачах (1) и (2). Именно, будем говорить, что план Х1 лучше плана Х2 при реализации с момента i, если
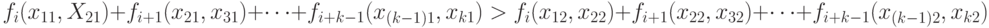 |
( 3) |
Будем писать 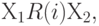 если выполнено неравенство (3), где
если выполнено неравенство (3), где 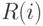 - бинарное отношение на множестве планов, задающее упорядочение планов отношением "лучше".
- бинарное отношение на множестве планов, задающее упорядочение планов отношением "лучше".
Ясно, что упорядоченность планов на  шагов, определяемая с помощью бинарного отношения
шагов, определяемая с помощью бинарного отношения 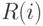 , может зависеть от
, может зависеть от  , т.е. "хорошесть" плана зависит от того, с какого момента
, т.е. "хорошесть" плана зависит от того, с какого момента  он начинает осуществляться. С точки зрения реальной экономики это вполне понятно. Например, планы действий, вполне рациональные для периода стабильного развития, никуда не годятся в период гиперинфляции. И наоборот, приемлемые в период гиперинфляции операции не принесут эффекта в стабильной обстановке.
он начинает осуществляться. С точки зрения реальной экономики это вполне понятно. Например, планы действий, вполне рациональные для периода стабильного развития, никуда не годятся в период гиперинфляции. И наоборот, приемлемые в период гиперинфляции операции не принесут эффекта в стабильной обстановке.
Однако, как легко видеть, в моделях с дисконтированием (2) все упорядочения 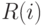 совпадают,
совпадают, 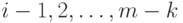 . Оказывается - это и есть основной результат настоящего подпункта - верно и обратное: если упорядочения совпадают, то мы имеем дело с задачей (2) - с задачей с дисконтированием, причем достаточно совпадения только при k=1,2. Сформулируем более подробно предположения об устойчивости упорядочения планов.
. Оказывается - это и есть основной результат настоящего подпункта - верно и обратное: если упорядочения совпадают, то мы имеем дело с задачей (2) - с задачей с дисконтированием, причем достаточно совпадения только при k=1,2. Сформулируем более подробно предположения об устойчивости упорядочения планов.
(I). Пусть 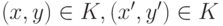 Верно одно из двух: либо
Верно одно из двух: либо
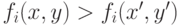
для всех 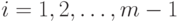 либо
либо

для всех 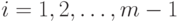
(II). Пусть 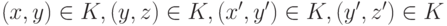 . Верно одно из двух: либо
. Верно одно из двух: либо
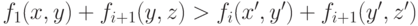
для всех 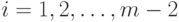 либо
либо
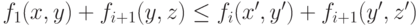
для всех 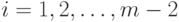
Как впервые подробно показано в работе [16], при некоторых внутриматематических условиях регулярности из условий устойчивости упорядоченности планов (I) и (II) следует существование констант 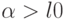 и
и 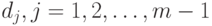 таких, что
таких, что

Поскольку прибавление константы не меняет точки, в которой функция достигает максимума, то последнее соотношение означает, что условия устойчивости упорядоченности планов (I) и (II) характеризуют (другими словами, однозначно выделяют) модели с дисконтированием среди всех моделей динамического программирования.
Как и в случае проблем устойчивости результата сравнения средних в теории измерений (см. "Основы теории измерений" ), проблему характеризации моделей с дисконтированием нетрудно выразить на языке общей схемы устойчивости. Речь идет о проблеме Б. Подробности оставляем читателю (см. также монографию [1]).
Математические условия, при которых доказывалась теорема о характеризации моделей с дисконтированием, постепенно ослаблялись на протяжении 1970-х годов (см. об этом в [1]), однако на экономическую сторону дела эти внутриматематические усовершенствования не влияли.
Асимптотически оптимальные планы. Рассмотрим модель (2) с 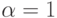
 |
( 4) |

При естественных математических предположениях, на которых не будем останавливаться, при каждом m существует оптимальный план 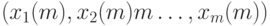 при котором достигает максимума оптимизируемая функция. Поскольку выбор горизонта планирования нельзя рационально обосновать, хотелось бы построить план действий, близкий к оптимальному при различных горизонтах планирования. Это значит, что целью является построение бесконечной последовательности
при котором достигает максимума оптимизируемая функция. Поскольку выбор горизонта планирования нельзя рационально обосновать, хотелось бы построить план действий, близкий к оптимальному при различных горизонтах планирования. Это значит, что целью является построение бесконечной последовательности 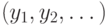 такой, что ее начальный отрезок длины
такой, что ее начальный отрезок длины  , т.е.
, т.е. 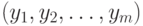 , дает примерно такое же значение оптимизируемого функционала, как и значение для оптимального плана
, дает примерно такое же значение оптимизируемого функционала, как и значение для оптимального плана 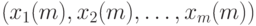 Бесконечную последовательность
Бесконечную последовательность 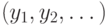 назовем асимптотически оптимальным планом.
назовем асимптотически оптимальным планом.
Выясним, можно ли использовать для построения асимптотически оптимального плана непосредственно оптимальный план. Зафиксируем k и рассмотрим последовательность 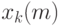 . Нетрудно построить примеры, показывающие, что, во-первых, элементы в этой последовательности будут меняться; во-вторых, они могут не иметь пределов. Следовательно, оптимальные планы могут вести себя крайне нерегулярно, а потому в таких случаях их нельзя использовать для построения асимптотически оптимальных планов.
. Нетрудно построить примеры, показывающие, что, во-первых, элементы в этой последовательности будут меняться; во-вторых, они могут не иметь пределов. Следовательно, оптимальные планы могут вести себя крайне нерегулярно, а потому в таких случаях их нельзя использовать для построения асимптотически оптимальных планов.
Тем не менее можно доказать (соответствующая экономико-математическая теория развита в "Многомерный статистический анализ" монографии [1]), что асимптотически оптимальные планы существуют, т.е. можно указать такие бесконечные последовательности , что
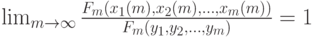
Таким образом решается проблема горизонта планирования - надо использовать асимптотически оптимальные планы, не зависящие от горизонта планирования. Интересно, что оптимальная траектория движения состоит из трех участков - начального, конечного и основного, а основной - это движение по магистрали. Полная аналогия с движением автотранспорта: чтобы попасть куда-либо, нужно сначала выехать на магистраль (шоссе), подъехать по хорошей дороге возможно ближе к цели, потом преодолеть заключительный участок.
