|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистический анализ числовых величин (непараметрическая статистика)
| Ранги | 1 | 2 | 3,5 | 3,5 | 5 | 6 | 7 | 8,5 | 8,5 | 10 | 11 | 12 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Элементы выборок | 0 | 1 | 2 | 2 | 3 | 5 | 6 | 7 | 7 | 11 | 13 | 14 | 15 |
| Номера выборок | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 | 2 | 1 | 1 | 1 |
| Ранги | 14 | 14 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Элементы выборок | 15 | 15 | 17 | 21 | 22 | 25 | 29 | 30 | 33 | 44 | 47 | 66 | 97 |
| Номера выборок | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 |
Хотя с точки зрения теории математической статистики вероятность совпадения двух элементов выборок равна 0, в реальных выборках экономических данных совпадения встречаются. Так, в рассматриваемых выборках, как видно из табл.1, два раза повторяется величина 2, два раза - величина 7 и три раза - величина 15. В таких случаях говорят о наличии "связанных рангов", а соответствующим совпадающим величинам приписывают среднее арифметическое тех рангов которые они занимают. Так, величины 2 и 2 занимают в объединенной выборке места 3 и 4, поэтому им приписывается ранг 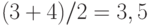 . Величины 7 и 7 занимают в объединенной выборке места 8 и 9, поэтому им приписывается ранг
. Величины 7 и 7 занимают в объединенной выборке места 8 и 9, поэтому им приписывается ранг 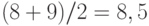 . Величины 15, 15 и 15 занимают в объединенной выборке места 13, 14 и 15, поэтому им приписывается ранг
. Величины 15, 15 и 15 занимают в объединенной выборке места 13, 14 и 15, поэтому им приписывается ранг 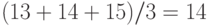 .
.
Следующий шаг - подсчет значения статистики Вилкоксона, т.е. суммы рангов элементов первой выборки
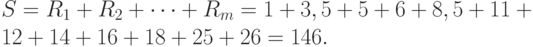
Подсчитаем также сумму рангов элементов второй выборки
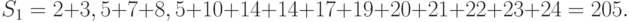
Величина 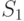 может быть использована для контроля вычислений. Дело в том, что суммы рангов элементов первой выборки
может быть использована для контроля вычислений. Дело в том, что суммы рангов элементов первой выборки  и второй выборки
и второй выборки 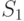 вместе составляют сумму рангов объединенной выборки, т.е. сумму всех натуральных чисел от 1 до
вместе составляют сумму рангов объединенной выборки, т.е. сумму всех натуральных чисел от 1 до  . Следовательно,
. Следовательно,

В соответствии с ранее проведенными расчетами  . Необходимое условие правильности расчетов выполнено. Ясно, что справедливость этого условия не гарантирует правильности расчетов.
. Необходимое условие правильности расчетов выполнено. Ясно, что справедливость этого условия не гарантирует правильности расчетов.
Перейдем к расчету статистики Т. Согласно формуле (3)
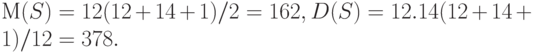
Следовательно,

Поскольку  , то гипотеза однородности принимается на уровне значимости0,05.
, то гипотеза однородности принимается на уровне значимости0,05.
Что будет, если поменять выборки местами, вторую назвать первой? Тогда вместо  надо рассматривать
надо рассматривать 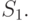 Имеем
Имеем
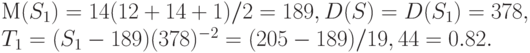
Таким образом, значения статистики критерия отличаются только знаком (можно показать, что это утверждение верно всегда). Поскольку в правиле принятия решения используется только абсолютная величина статистики, то принимаемое решение не зависит от того, какую выборку считаем первой, а какую второй. Для уменьшения объема таблиц принято считать первой выборку меньшего объема.
Продолжим обсуждение критерия Вилкоксона. Правила принятия решений и таблица критических значений для критерия Вилкоксона строятся в предположении справедливости гипотезы полной однородности, описываемой формулой (2). А что будет, если эта гипотеза неверна? Другими словами, какова мощность критерия Вилкоксона?
Пусть объемы выборок достаточно велики, так что можно пользоваться асимптотической нормальностью статистики Вилкоксона. Тогда в соответствии с формулами (1) статистика T будет асимптотически нормальна с параметрами
![М(T) = ( 12mn )^{ ?} (1/2 - a) (m+n+1)^{ - ?} ,
D(T) = 12 [(n - 1) b^2 + (m - 1) g^2 + a(1 -a) ] (m+n+1)^{ - 1}](/sites/default/files/tex_cache/7f8adc5904c4bcce606c8cb95658ea96.png) |
( 5) |
Из формул (5) видно большое значение гипотезы
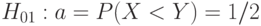 |
( 6) |
Если эта гипотеза неверна, то, поскольку  , справедлива оценка
, справедлива оценка
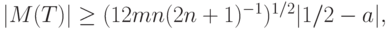
а потому 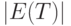 безгранично растет при росте объемов выборок. В то же время, поскольку
безгранично растет при росте объемов выборок. В то же время, поскольку
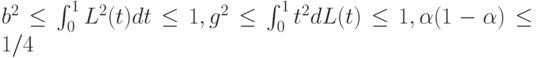
то
![D(T) \le 12 [(n - 1) + (m - 1) + 1/4] (m+n+1)^{ - 1} \le 12](/sites/default/files/tex_cache/ba8391d1fa7b39755713b0f3a06a8e98.png) |
( 7) |
Следовательно, вероятность отклонения гипотезы H01 , когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (6), стремится к 1 при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе
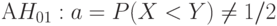 |
( 8) |
Если же гипотеза (6) верна, то статистика T асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой
![D(T) = 12 [(n - 1) b^2 + (m - 1) g^2 + 1/4 ] (m+n+1)^{-1}](/sites/default/files/tex_cache/bcae5545c281b36e1dd20e796bb30609.png) |
( 9) |
Гипотеза (6) является сложной, дисперсия (9), как показывают приводимые ниже примеры, в зависимости от значений 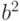 и
и 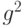 может быть как больше 1, так и меньше 1, но согласно неравенству (7) никогда не превосходит 12.
может быть как больше 1, так и меньше 1, но согласно неравенству (7) никогда не превосходит 12.
Приведем пример двух функций распределения  и
и 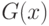 таких, что гипотеза (6) выполнена, а гипотеза (2) - нет. Поскольку
таких, что гипотеза (6) выполнена, а гипотеза (2) - нет. Поскольку
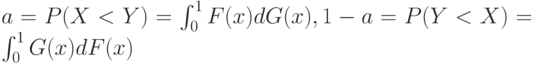
и 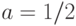 в случае справедливости гипотезы (2), то для выполнения условия (6) необходимо и достаточно, чтобы
в случае справедливости гипотезы (2), то для выполнения условия (6) необходимо и достаточно, чтобы
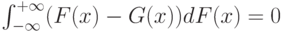 |
( 10) |
а потому естественно в качестве  рассмотреть функцию равномерного распределения на интервале (-1 ; 1). Тогда формула (11) переходит в условие
рассмотреть функцию равномерного распределения на интервале (-1 ; 1). Тогда формула (11) переходит в условие
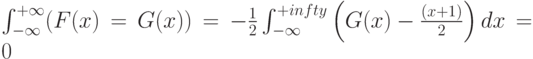 |
( 11) |
Это условие выполняется, если функция 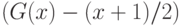 является нечетной.
является нечетной.
Пример 2. Пусть функции распределения  и
и 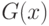 сосредоточены на интервале
сосредоточены на интервале 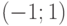 , на котором
, на котором

Тогда
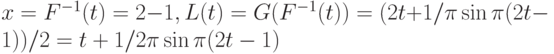
Условие (11) выполнено, поскольку функция 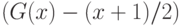 является нечетной. Следовательно,
является нечетной. Следовательно, 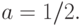 Начнем с вычисления
Начнем с вычисления
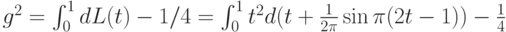
Поскольку
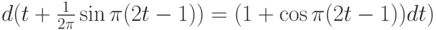
то
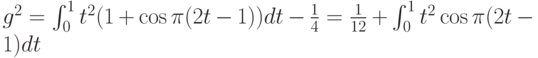
С помощью замены переменных  получаем, что
получаем, что

В правой части последнего равенства стоят табличные интегралы (см., например, справочник [14, с.71]. Проведя соответствующие вычисления, получаем, что в правой части стоит 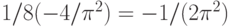 . Следовательно,
. Следовательно,

Перейдем к вычислению 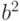 . Поскольку
. Поскольку
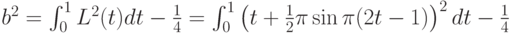
то
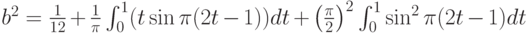
С помощью замены переменных 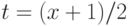 переходим к табличным интегралам (см., например, справочник [14, с.65]):
переходим к табличным интегралам (см., например, справочник [14, с.65]):
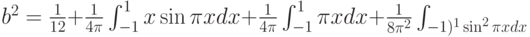
Проведя необходимые вычисления, получим, что
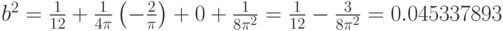
Следовательно, для рассматриваемых функций распределения нормированная и центрированная статистика Вилкоксона (см. формулу (4)) асимптотически нормальна с математическим ожиданием 0 и дисперсией (см. формулу (9))

Как легко видеть, дисперсия всегда меньше 1. Это значит, что в рассматриваемом случае гипотеза полной однородности (2) при проверке с помощью критерия Вилкоксона будет приниматься чаще, чем если она на самом деле верна.
На наш взгляд, это означает, что критерий Вилкоксона нельзя считать критерием для проверки гипотезы (2) при альтернативе общего вида. Он не всегда позволяет проверить однородность - не при всех альтернативах. Точно так же критерии типа хи-квадрат нельзя считать критериями проверки гипотез согласия и однородности - они позволяют обнаружить не все различия, поскольку некоторые из них "скрадывает" группировка.
Обсудим теперь, действительно ли критерий Вилкоксона нацелен на проверку равенства медиан распределений, соответствующих выборкам.
Пример 3. Построим семейство пар функций распределения  и
и 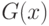 таких, что их медианы различны, но для
таких, что их медианы различны, но для  и
и 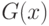 выполнена гипотеза (6). Пусть распределения сосредоточены на интервале
выполнена гипотеза (6). Пусть распределения сосредоточены на интервале 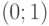 , и на нем
, и на нем 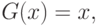 а
а  имеет кусочно-линейный график с вершинами в точках
имеет кусочно-линейный график с вершинами в точках 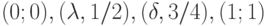 . Следовательно,
. Следовательно,
 при
при  ;
;
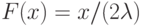 на
на 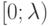 ;
;
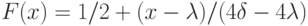 на
на 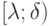 ;
;
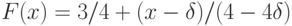 на
на ![[\delta; 1]](/sites/default/files/tex_cache/99c26672f22f59edc51a4afea3549acd.png) ;
;
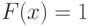 при
при  .
.
Очевидно, что медиана  равна
равна  , а медиана
, а медиана 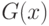 равна 1/2 .
равна 1/2 .
Согласно соотношению (9) для выполнения гипотезы (6) достаточно определить  как функцию
как функцию 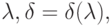 из условия
из условия
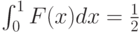
Вычисления дают
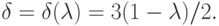
Учитывая, что  лежит между
лежит между  и 1, не совпадая ни с тем, ни с другим, получаем ограничения на
и 1, не совпадая ни с тем, ни с другим, получаем ограничения на  , а именно,
, а именно, 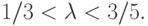 Итак, построено искомое семейство пар функций распределения.
Итак, построено искомое семейство пар функций распределения.
