Амортизация
4.4 Метод фиксированного процента
Метод постоянного или фиксированного процентаМФП2На английском языке - Declining-Balance Depreciation. состоит в том, что в конце каждого года стоимость, которую имущество имело в начале года, снижается на одно и то же число процентов от этой стоимости.
Выведем формулу для определения балансовой стоимости имущества на конец k-го года при амортизации по МФП. Обозначим через r фиксированную ставку процента (десятичная дробь), на которую снижается балансовая стоимость имущества каждый год. В конце первого года эта стоимость снизится на Sr и станет равна
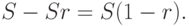
В конце второго года эта стоимость снизится на S(1-r)r и станет равна
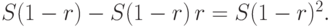
Продолжая такое рассуждение, получим, что стоимость имущества в конце k-го года  вычисляется по формуле:
вычисляется по формуле:

Из формулы (4.6) видно, что балансовая стоимость имущества не может стать равной 0, не зависимо от срока его службы.
Если срок службы имущества составляет n лет и его остаточная стоимость равна  , то можно определить число процентов r, на которое следует снижать стоимость каждый год, из уравнения:
, то можно определить число процентов r, на которое следует снижать стоимость каждый год, из уравнения: 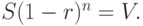 Решая последнее уравнение относительно r, получаем формулу:
Решая последнее уравнение относительно r, получаем формулу:
![r=1-\sqrt[n]{\frac{V}{S}}\,\,\, (4.7)](/sites/default/files/tex_cache/218019bb295556c3e9a95b646650f606.png)
Заметим, что формула (4.6) является вариантом формулы для вычисления наращенной суммы при начислении сложных процентов, когда начисленные проценты не прибавляются к начальной сумме, а вычитаются из нее.
Метод фиксированного процента называют еще методом геометрической прогрессии, так как значения балансовой стоимости имущества по годам образуют убывающую геометрическую прогрессию с первым членом, равным S, и знаменателем, равным  .
.
Отметим, что метод фиксированного процента имеет две вычислительные особенности. Во-первых, фиксированный процент r трудно вычислить, не имея под рукой хотя бы калькулятор со встроенной функцией возведения числа в произвольную степень3Напомним читателю, что ![\sqrt[n]{x}=x^{1/n}.](/sites/default/files/tex_cache/4a4f488f0c786bcfdd20fae1fcd5c0eb.png) . Во-вторых, балансовая стоимость имущества не может быть снижена до нуля, так как все члены последовательности
. Во-вторых, балансовая стоимость имущества не может быть снижена до нуля, так как все члены последовательности  при 0<r<1 положительны. Этих особенностей нет у метода двойного процента, который будет изложен в следующем пункте.
при 0<r<1 положительны. Этих особенностей нет у метода двойного процента, который будет изложен в следующем пункте.
Пример 43. Составим таблицу амортизации стоимости прибора из примера 41 при применении метода фиксированного процента.
Решение. По формуле (4.7) вычислим фиксированный процент амортизации:
![r=1-\sqrt[10]{\frac{10\,000}{110\,000}}=1-0.7868=0.2132=21.32\%.](/sites/default/files/tex_cache/666f535ceea69aa90be90fa13f2f8df7.png)
Теперь составим таблицу амортизационных отчислений и балансовых стоимостей прибора по годам. Используя эту таблицу, построим график изменения балансовой стоимости прибора по годам при амортизации по МФП (рис. 10). Как и в предыдущем примере, на оси абсцисс будем откладывать периоды эксплуатации (годы), а на оси ординат - значения балансовой стоимости в конце соответствующего года.
| Год службы | Амортизационные отчисления (руб.) | Стоимость на конец года (руб.) |
|---|---|---|
| 0 | 0 | 110 000 |
| 1 | 110 000 x 0.2132 = 23 453 | 86 547 |
| 2 | 86 547 x 0.2132 = 18 452 | 68 095 |
| 3 | 68 095 x 0.2132 = 14 518 | 53 577 |
| 4 | 53 577 x 0.2132 = 11 423 | 42 154 |
| 5 | 42 154 x 0.2132 = 8 967 | 33 166 |
| 6 | 33 166 x 0.2132 = 7 071 | 26 095 |
| 7 | 26 095 x 0.2132 = 5 564 | 20 531 |
| 8 | 20 531 x 0.2132 = 4 377 | 16 154 |
| 9 | 16 154 x 0.2132 = 3 444 | 12 710 |
| 10 | 12 710 x 0.2132 = 2 710 | 10 000 |
Объясним, какая математическая функция соответствует графику, приведенному на рис. 10. Из уравнения (4.6) следует, что график балансовой стоимости амортизируемого объекта является дугой графика показательной функции, которая соединяет точку с координатами (0,S) на оси ординат с точкой с координатами 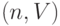
Сравним изменение балансовой стоимости прибора по годам при амортизации по МФП (пример 43) и при амортизации по ПСЛ (пример 42). Результаты сравнения удобно представить в виде таблицы:
| Год службы | Стоимость на конец года (МФП) (руб.) | Стоимость на конец года (ПСЛ) (руб.) | Разность (%) |
|---|---|---|---|
| 0 | 110 000 | 110 000 | 0 |
| 1 | 86 547 | 91 818 | 5.74 |
| 2 | 68 095 | 75 455 | 9.75 |
| 3 | 53 577 | 60 909 | 12.04 |
| 4 | 42 154 | 48 182 | 12.51 |
| 5 | 33 166 | 37 273 | 11.02 |
| 6 | 26 095 | 28 182 | 7.40 |
| 7 | 20 531 | 20 909 | 1.81 |
| 8 | 16 154 | 14 555 | -4.53 |
| 9 | 12 710 | 11 818 | -7.54 |
| 10 | 10 000 | 10 000 | 0.00 |
Сравнивая значения во втором и третьем столбцах последней таблицы, замечаем, что амортизация по МФП происходит быстрее: за исключением 8-го и 9-го годов, стоимость прибора на конец года при амортизации по МФП меньше, чем при ПСЛ. Например, к концу четвертого года при амортизации по ПСЛ стоимость прибора равна 48 182 руб., а при амортизации по МФП - 42 154 руб., что меньше на 12.51%.


