Простые проценты
2.3 Банковский депозит под простые проценты
Формула (8) связывает между собой четыре величины: S, P, r и t. С помощью этой формулы, выделив любые три из них и задав их значения, можно вычислить значение четвертой величины. Таким образом, имеем четыре типа задач, соответствующих четырём возможным способам выделения трех объектов из четырех: определение величины наращенной суммы, определение величины необходимой исходной суммы, определение необходимого срока хранения и определение процента. Приведем примеры.
Пример 24. Банк выплачивает 6% простых в год. Господин Федоров хочет получить через 2 года и 6 месяцев 10,000 руб. на подарок сыну к 16-летию. Вычислим, какую сумму он должен положить в банк в настоящий момент.
Решение. Нам дано: 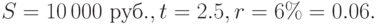 Из формулы (2.1) получаем формулу для вложенной суммы:
Из формулы (2.1) получаем формулу для вложенной суммы:

Подставляя данные задачи в эту формулу, получаем ответ:

Пример 25. В банк было положено 1,500 руб. Через 1 год 3 месяца на счете было 1,631.25 руб. Определим, сколько простых процентов в год выплачивает банк.
Решение. Нам дано:P=1,500 руб.,t=1.25, S=1,631.25 руб.
Из формулы (2.1) получаем формулу для r:
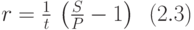
Подставляем данные задачи в эту формулу:
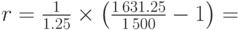
Пример 26. В банке был открыт депозитный счёт, на который было положено 1,500 руб. под 7% простых. Через некоторое время на счёте стало 1,631.25 руб. Определим, сколько времени прошло с момента открытия счёта.
Решение. Нам дано: P=1,500 руб., r=7% и S=1,631.25 руб.
Из формулы (2.1) получаем формулу для t:
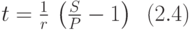
Подставляем данные задачи в эту формулу:
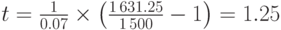
2.4 Процентный пункт
Изменения ставки процента часто указывается в процентных пунктах. Если говорят, что ставка процента, равная r%, увеличилась на i процентных пункта, то это означает, что новое значение ставки процента составляет (r+i)\%. Таким образом, если процентная ставка r=3\% увеличилась на 0.5 процентных пункта, то новое значение процентной ставки r составляет 3.5%. Это изменение можно охарактеризовать и в процентах от начального значения ставки (3%). Тогда следует указать, что процентная ставка увеличилась на

Однако в последнее время банки гораздо чаще уменьшают процентные ставки по вкладам. Если процентная ставка по вкладу составляла 10% и была уменьшена до 4%, то можно сказать, что процентная ставка была уменьшена на 6 процентных пунктов. Это изменение также можно охарактеризовать в процентах от начального значения ставки (10%). Тогда следует указать, что процентная ставка уменьшилась на
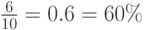
Как видно из приведенных примеров, задание изменения ставки процента в процентных пунктах является удобным и предполагает более простые вычисления (только сложение или вычитание).
2.5 Векселя
Вексель - ценная бумага, являющаяся простейшим типом долгового обязательства. Слово вексель является калькой с немецкого глагола Wechseln, который означает менять. Простой вексель представляет из себя безусловное письменное обязательство одного лица выплатить определенную сумму денег другому лицу в указанную дату или по первому требованию. Поэтому все векселя именные и выпускаются в бумажном виде. Процедура получения денег по векселю называется его гашением.
Вексель имеет очень долгую историю - еще в Древней Греции и Риме употреблялись документы, похожие на современные векселя. Широко применялись векселя и в дореволюционной России. Для тех, кто заинтересуется историей этого вопроса, рекомендуем почитать главы, посвящённые векселям, в "Курсе коммерческой арифметики и торговых операций" (А. Мансфельд, Москва, 1907 г.).
В 1930 г. ряд стран заключили Женевскую вексельную конвенцию, которая установила Единообразный закон о переводном и простом векселях. СССР ратифицировал Женевскую вексельную конвенцию в 1937 г. и ввел в действие положение о переводном и простом векселе. Текст этого положения является переводом на русский язык Единообразного закона. Из-за жесткого государственного регулирования средств предприятий вексельное положение в СССР не получили практического применения.
Положение существенно поменялось в последнее десятилетие 20 века: в России не только действует положение о переводном и простом векселе, но векселя довольно широко используются хозяйствующими субъектами.
К преимуществам векселей (перед депозитами, например) можно отнести возможность их использования в качестве расчетного средства (при крупных покупках) и залога (при получении кредита). Также вексель можно предать другому лицу или продать на вторичном рынке. Однако следует иметь в виду, что использование векселей имеет и ряд неудобств. Главное, по нему довольно сложно досрочно получить деньги: лицо, выписавшее вексель, не обязано досрочно гасить его.
Векселя не торгуются на биржах, поэтому у них нет официальных котировок. Узнать средние цены каждого векселя можно в различных информационных системах, например, в российской вексельной системе http://www.bills.ru. Доход по векселю может выплачиваться в момент его погашения в виде фиксированного процента, если вексель покупался по номинальной стоимости. Сейчас на рынке в основном обращаются дисконтные векселя, которые гасятся по номинальной стоимости, а продаются по меньшей цене - с дисконтом. Рассмотрим пример.
Пример 27. Г-н Иванов занял у г-на Петрова деньги, получив от него 9,800 руб. и выдал ему вексель, по которому обязался выплатить 10,000 руб. через три месяца. Определим, под какой годовой процент r выдан этот вексель?
Решение. Применим формулу (2.3) при P=9,800, S=10,000, t=0.25: