|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Приложение 1: Векторное пространство
Скалярное произведение векторов
Скалярным произведением векторов  и
и  называется число (скаляр), обозначаемое как (
называется число (скаляр), обозначаемое как (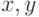 ) (или просто
) (или просто 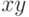 ) и определяемое соотношением
) и определяемое соотношением
Основными свойствами этой операции являются:
- симметрия
 ;
; - дистрибутивность
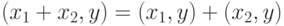 ;
; -
 для любого вещественного
для любого вещественного  ;
; -
 , причем
, причем 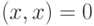 тогда и только тогда, когда
тогда и только тогда, когда 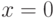 .
.
Величина 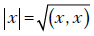 называется модулем(длиной)вектора x.
называется модулем(длиной)вектора x.
Для любых двух векторов  и
и  справедливо неравенство Коши-Буняковского
справедливо неравенство Коши-Буняковского  .
.
Векторы  и
и  называются коллинеарными, если
называются коллинеарными, если  . Практически это означает, что координаты этих векторов пропорциональны.
. Практически это означает, что координаты этих векторов пропорциональны.
Векторы  и
и  называются ортогональными, если их скалярное произведение равно нулю:
называются ортогональными, если их скалярное произведение равно нулю: 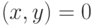 .
.
Вещественное линейное пространство называется евклидовым пространством, если в нем определено скалярное произведение элементов. В евклидовом пространстве удобно использовать базис  , все элементы которого взаимно ортогональны и имеют единичную длину, т.е.
, все элементы которого взаимно ортогональны и имеют единичную длину, т.е.

где  - символ Кронекера.
- символ Кронекера.
Такие базисы называются ортонормированными и существуют в любом евклидовом пространстве. В ортонормированном базисе координаты вектора  можно представить в виде
можно представить в виде 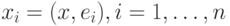 , а разложение вектора по базису как
, а разложение вектора по базису как
Введение в рассмотрение скалярного произведения позволяет в дальнейшем использовать такие геометрически содержательные понятия, как ортогональность, угол и длина. Эти свойства широко используются при объяснении (обосновании и изложении) метода наименьших квадратов (МНК), в частности, при получении системы нормальных уравнений, а также для объяснения свойств МНК-оценок.


