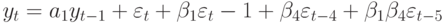|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Стационарные временные ряды, модели авторегрессии - скользящего среднего
10.9. Учет сезонности в модели
Многие экономические процессы, особенно в сельском хозяйстве и туристическом секторе в том или ином смысле обладают сезонной цикличностью. Предновогодние распродажи также обязательно должны быть приняты во внимание в период прогнозирования временного ряда розничных продаж. Итак, сезонная вариация некоторых экономических рядов может превышать их общую вариацию. Прогнозы, которые не учитывают сезонную цикличность, могут быть неудовлетворительными.
Техника учета сезонной цикличности для АРСС-моделей в принципе не отличается от обычного подхода. Если существует сезонная цикличность с периодом s-шагов, то ненулевые сезонные АКФ и ЧАКФ появятся при запаздываниях 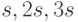 скорее, чем при
скорее, чем при 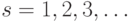
На практике построение модели затруднительно, так как сезонные отрезки временного ряда будут взаимодействовать с несезонными отрезками временного ряда. Поэтому АКФ и ЧАКФ для комбинированных временных рядов будут отражать это взаимодействие.
Многие исследователи предпочитают мультипликативное представление сезонной модели, так как богатый спектр взаимодействий может быть отражен в компактной модели с малым числом коэффициентов.
Выпишем модель
Оценивая три коэффициента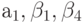 , отразим эффект авторегрессии и эффекты моделей скользящего среднего с лагами 1, 4 и 5. Коэффициенты скользящего среднего оказываются взаимосвязанными. Оценивая более сложную модель вида
, отразим эффект авторегрессии и эффекты моделей скользящего среднего с лагами 1, 4 и 5. Коэффициенты скользящего среднего оказываются взаимосвязанными. Оценивая более сложную модель вида

можно получить меньшую сумму квадратов остатков модели, так как 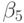 в этом случае не связано соотношением
в этом случае не связано соотношением 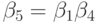 . Однако (10.51) является более экономичной моделью и на экзаменационной выборке может показать не худшие результаты прогноза.
. Однако (10.51) является более экономичной моделью и на экзаменационной выборке может показать не худшие результаты прогноза.
В заключение отметим, что не существует теоретических исследований, доказывающих преимущества одной формулы представления сезонных компонент в модели перед возможными другими формулами.
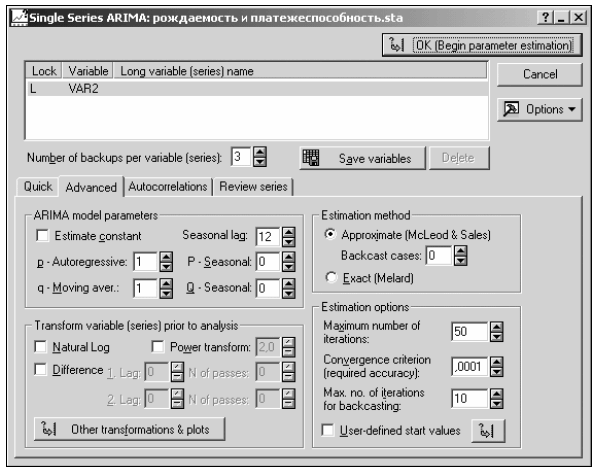
Построение моделей авторегрессии интегрированного скользящего среднего (АРИСС) автоматизировано в популярных статистических пакетах. Например, в пакете STATISTICA в модуле "Временные ряды", заставка которого выглядит следующим образом (рис. 10.1).
Контрольные вопросы
- Дайте определения стационарного в слабом смысле стохастического процесса.
- Как определяются автокорреляции временного ряда?
- Как записать АРСС(
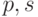 )-модель для стационарного временного ряда?
)-модель для стационарного временного ряда? - Выпишите условия стационарности для процессов АР(1), АР(2), АРСС(1, 1).
- Как получить расчетные формулы для частных автокорреляций ряда (ЧАКФ) по методу Юла - Уокера?
- В чем отличие поведения АКФ и ЧАКФ для авторегрессии и для процессов скользящего среднего?
- Как тестировать адекватность моделей и находить порядок
 скользящего среднего с помощью статистик Бокса - Пирса и Льюиса - Бокса?
скользящего среднего с помощью статистик Бокса - Пирса и Льюиса - Бокса? - Какие есть еще приемы селекции моделей АРСС(
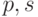 )?
)? - В чем состоит принцип выбора экономичной модели?
- Как учитывают явления сезонности в моделях АРСС(
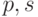 )?
)? - Покажите, что АКФ для СС(2)-процесса
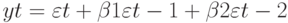 имеет два ненулевых значения
имеет два ненулевых значения 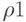 и
и 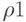 , а остальные
, а остальные 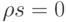 , для
, для 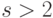 .
. - Постройте коррелограмму для АРСС(2, 1)-модели. Для общих АРСС(
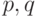 )-моделей, начиная с запаздывания
)-моделей, начиная с запаздывания  , значения
, значения 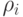 будут удовлетворять уравнению
будут удовлетворять уравнению
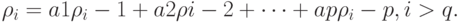
При этом первые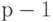 значения
значения 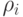 трактуются как начальные условия, получаемые из уравнений Юла - Уокера.
трактуются как начальные условия, получаемые из уравнений Юла - Уокера.