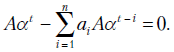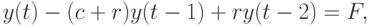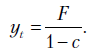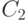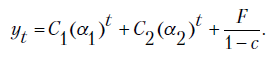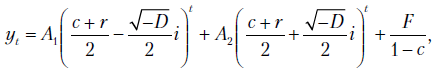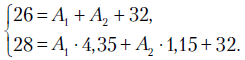|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Разностные уравнения и их решение
9.2. Системы разностных уравнений более высокого порядка
Тот же метод может быть использован для решения однородных систем разностных уравнений более высокого порядка.
Однородное разностное уравнение для (9.2) имеет вид
Здесь также можно ожидать, что каждое решение (9.12) представимо в виде  где
где - произвольная постоянная. Чтобы найти возможные значения
- произвольная постоянная. Чтобы найти возможные значения  , решим уравнение
, решим уравнение
После деления обеих его частей на 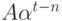 , получаем:
, получаем:
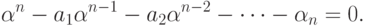
Многочлен  -го порядка, стоящий в левой части последнего равенства, имеет
-го порядка, стоящий в левой части последнего равенства, имеет  корней
корней 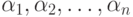 . Можно показать, что линейная комбинация решений уравнения (9.12)
. Можно показать, что линейная комбинация решений уравнения (9.12)
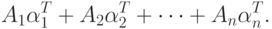
будет также его решением. Произвольные постоянные  вычисляются подстановкой
вычисляются подстановкой  начальных условий в общее решение. Числа
начальных условий в общее решение. Числа 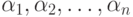 могут быть как действительными, так и комплексными. Условия устойчивости (отсутствие роста решения до бесконечности) требуют, чтобы действительные характеристические корни были по абсолютной величине меньше единицы. Для комплексных корней условие устойчивости заключается в том, чтобы все они находились внутри единичного круга комплексной плоскости. Необходимым условием нахождения характеристических корней в единичном круге является выполнение соотношения
могут быть как действительными, так и комплексными. Условия устойчивости (отсутствие роста решения до бесконечности) требуют, чтобы действительные характеристические корни были по абсолютной величине меньше единицы. Для комплексных корней условие устойчивости заключается в том, чтобы все они находились внутри единичного круга комплексной плоскости. Необходимым условием нахождения характеристических корней в единичном круге является выполнение соотношения 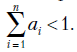 Достаточным условием нахождения характеристических корней в единичном круге является выполнение соотношения
Достаточным условием нахождения характеристических корней в единичном круге является выполнение соотношения 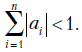 По крайней мере один из характеристических корней равен единице, если
По крайней мере один из характеристических корней равен единице, если
Нахождение частных решений
1. Пусть в (9.2) 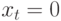 . Тогда
. Тогда  . Попробуем частное решение найти в виде постоянной. Подставляя
. Попробуем частное решение найти в виде постоянной. Подставляя  , получаем
, получаем
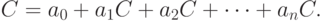
Если  , то решение найдено. Если же
, то решение найдено. Если же  , то
, то  не определяется. В этом случае попытаемся найти частное решение в другом виде. Вспомним, что в данной ситуации
не определяется. В этом случае попытаемся найти частное решение в другом виде. Вспомним, что в данной ситуации 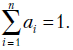 и
и  - расходящаяся последовательность. Попробуем получить решение в виде линейной функции (тренда) от времени
- расходящаяся последовательность. Попробуем получить решение в виде линейной функции (тренда) от времени  , т.е. в виде
, т.е. в виде 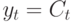 . Получаем уравнение
. Получаем уравнение
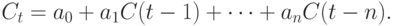
Раскрыв скобки, имеем:

Учитывая, что  , в случае
, в случае 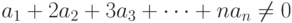 получаем решение
получаем решение
В противном случае ищем решение в виде функций:  Для уравнения
Для уравнения  -го порядка одна из этих функций обязательно будет частным решением.
-го порядка одна из этих функций обязательно будет частным решением.
2. Пусть в (9.2) 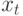 имеет экспоненциальную форму
имеет экспоненциальную форму 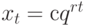 . Частное решение ищут в виде
. Частное решение ищут в виде 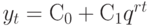 , где
, где и
и являются константами. Подставляя в уравнение это предполагаемое решение, получаем
являются константами. Подставляя в уравнение это предполагаемое решение, получаем
![С_{0} + С_{1}q^{rt} = a_{0} + a_{1}[С_{0} + С_{1}q^{r(t - 1)}] + сq^{rt}.](/sites/default/files/tex_cache/9cdb13adc39a7536f6b1f9a7749be7a8.png)
Приравнивая соответствующие слагаемые (константы приравниваем константам, слагаемые с ростом r в левой части равенства - слагаемым с тем же ростом в правой части равенства), получаем частное решение в виде
Отметим, что при  решение (9.13) сходится с ростом
решение (9.13) сходится с ростом  к постоянной
к постоянной 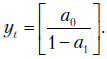
Если 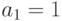 , то выбираем
, то выбираем , а если
, а если  , то
, то 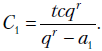
3. Пусть  , где
, где - константа, а
- константа, а  - положительное целое число. Следовательно,
- положительное целое число. Следовательно,
Частное решение следует искать в виде общего многочлена степени  от времени
от времени  :
:
Чтобы найти коэффициенты 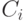 , подставим (9.15) в (9.14). В полученном равенстве надо приравнять коэффициенты при одинаковых степенях
, подставим (9.15) в (9.14). В полученном равенстве надо приравнять коэффициенты при одинаковых степенях  и получить равенства для определения
и получить равенства для определения 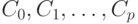 . Для простоты предположим, что
. Для простоты предположим, что  (этого достаточно для подавляющего большинства экономических приложений), и рассмотрим разностное уравнение второго порядка
(этого достаточно для подавляющего большинства экономических приложений), и рассмотрим разностное уравнение второго порядка 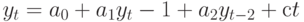 . Частное решение представим в виде
. Частное решение представим в виде 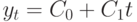 . Подставляя частное решение в уравнение, имеем:
. Подставляя частное решение в уравнение, имеем:
![C_{0} + C_{1}t = a_{0} + a_{1}[C_{0} + C_{1}(t - 1)] + a_{2}[C_{0} + C_{1}(t - 2)] + ct.](/sites/default/files/tex_cache/09e581711d0228fa8cb070e11c6969aa.png)
Приравнивая слева и справа постоянные и члены с множителем  , получаем:
, получаем:
Если  , то нужно умножить частное решение на
, то нужно умножить частное решение на  и искать коэффициенты
и искать коэффициенты 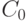 и
и 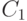 тем же способом.
тем же способом.
Рассмотрим пример, в котором разностные уравнения используются для изучения эффекта взаимодействия потребительского спроса и спроса на инвестиции.
Изучается односекторная модель экономики, в которой существуют три составные части общего спроса: потребительский спрос, спрос на инвестиции и правительственные расходы.
Пусть потребление в год с номером  обозначено через
обозначено через 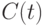 и линейно зависит от дохода в предыдущий период
и линейно зависит от дохода в предыдущий период 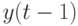 :
:
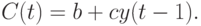
Ожидаемый общий спрос в году 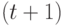 обозначим
обозначим 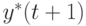 . Пусть оптимальное соотношение "капитал - выпуск" равно
. Пусть оптимальное соотношение "капитал - выпуск" равно  . Тогда количество капитала, требуемого для удовлетворения ожидаемого общего спроса, равно
. Тогда количество капитала, требуемого для удовлетворения ожидаемого общего спроса, равно 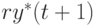 . Следовательно, к началу
. Следовательно, к началу 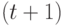 -го года количество капитала составит
-го года количество капитала составит
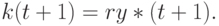
Инвестиции в течение года  должны контролировать процесс накопления капитала от
должны контролировать процесс накопления капитала от 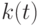 в начальный период года
в начальный период года  до
до  , требуемого в начальный период
, требуемого в начальный период 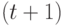 -го года. Если игнорировать амортизацию капитала, то инвестиции в год
-го года. Если игнорировать амортизацию капитала, то инвестиции в год  равны
равны
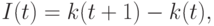
поэтому
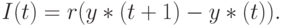
Предположим, что существует запаздывание (лаг) величиной в один год между заказом на инвестиции и их выполнением, т.е. те капиталовложения, которые готовы приносить отдачу в период  , должны быть заказаны в период
, должны быть заказаны в период  , когда известно только значение общего спроса
, когда известно только значение общего спроса 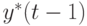 .
.
Предположим, что ожидаемый общий спрос в будущем 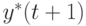 приравнивается известному общему спросу в настоящий момент, т.е.:
приравнивается известному общему спросу в настоящий момент, т.е.:
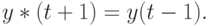
Отсюда
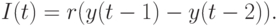
Допустим, правительственные расходы не изменяются от периода к периоду, т.е.:
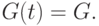
Предположения  в совокупности дают общий спрос в период
в совокупности дают общий спрос в период  . Предполагая, что общий спрос равен общему доходу, получаем:
. Предполагая, что общий спрос равен общему доходу, получаем:
![y(t) = cy(t - 1) + r[y(t - 1) - y(t - 2)] + b + G.](/sites/default/files/tex_cache/e98bafcbab5d73066641bdfb5b102995.png)
После упрощений имеем:
где 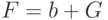 - экзогенная (внешняя), не зависящая от времени постоянная.
- экзогенная (внешняя), не зависящая от времени постоянная.
Выражение (9.16) является линейным неоднородным разностным уравнением второго порядка. Характеристическое уравнение для него имеет вид
Прежде всего напомним, что частное решение при постоянной правой части 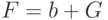 равно
равно
Далее рассмотрим три случая.
Случай 1. 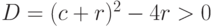 . Здесь
. Здесь 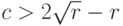 . Тогда общее решение однородного уравнения
. Тогда общее решение однородного уравнения

имеет вид
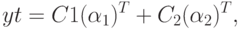
где
Представим общее решение:
Если  и
и  то с течением времени общий доход
то с течением времени общий доход  стремится к величине
стремится к величине 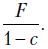 Но если хотя бы один из корней
Но если хотя бы один из корней 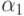 или
или 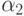 по абсолютной величине превышает 1 и начальные условия таковы, что
по абсолютной величине превышает 1 и начальные условия таковы, что и
и не равны нулю, то с течением времени будет наблюдаться рост дохода.
не равны нулю, то с течением времени будет наблюдаться рост дохода.
Случай 2. 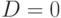 , тогда
, тогда  , или
, или 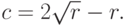 В этом случае
В этом случае
C течением времени при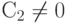 может наблюдаться некоторый рост общего дохода. Однако множитель
может наблюдаться некоторый рост общего дохода. Однако множитель 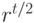 при
при  , и доход стабилизируется, приближаясь к
, и доход стабилизируется, приближаясь к 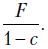
Случай 3.  или
или 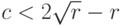 . В этом случае общее решение можно получить либо с использованием комплексных корней характеристического уравнения
. В этом случае общее решение можно получить либо с использованием комплексных корней характеристического уравнения
либо, обращаясь к теореме Муавра о представлении комплексных чисел, - в тригонометрическом виде
Рассмотрим пример. Пусть доля общего дохода, идущего на потребление (предельная склонность к потреблению),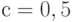 , а отношение "капитал - выпуск"
, а отношение "капитал - выпуск" 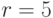 . Кроме того, правительственные расходы
. Кроме того, правительственные расходы  и постоянный потребительский спрос
и постоянный потребительский спрос 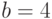 . Найдем доход в течение последующих периодов времени, если начальный доход
. Найдем доход в течение последующих периодов времени, если начальный доход 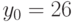 , а доход после первого года
, а доход после первого года 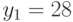 .
.
Выпишем характеристическое уравнение (9.17)
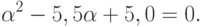
Решая его, получаем 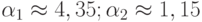 .
.
Представим общее решение разностного уравнения в виде
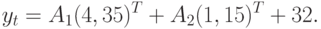
C учетом начальных условий находим 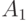 и
и 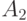 . Получаем систему
. Получаем систему
Отсюда 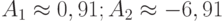 . Исходя из этого решение принимает вид
. Исходя из этого решение принимает вид

Очевидно, что для больших значений  рост будет в основном определяться первым слагаемым.
рост будет в основном определяться первым слагаемым.
Контрольные вопросы
- Как определить первую разность для функции
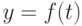 ?
? - Запишите линейное неоднородное разностное уравнение
 -го порядка с постоянными коэффициентами.
-го порядка с постоянными коэффициентами. - Как свести модель Кейнса - Самуэльсона производства и потребления к линейному неоднородному разностному уравнению для производственной функции
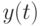 ?
? - Выпишите модель случайных блужданий (random walk model).
- Как получить решение неоднородного разностного уравнения первого порядка методом итераций?
- Запишите характеристическое уравнение для однородного разностного уравнения второго порядка.
- Рассмотрите три случая построения решений для однородных разностных уравнений второго порядка.
- Рассмотрите три случая построения частных решений для неоднородного разностного уравнения второго порядка.
- Сформулируйте условия устойчивости (решение не стремится к бесконечности) для разностных уравнений различных порядков.
- Рассмотрите два случая:
-
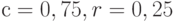 . Остальные предположения оставьте теми же, что в численном примере (п. 9.2);
. Остальные предположения оставьте теми же, что в численном примере (п. 9.2); -
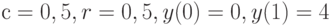 ; при
; при 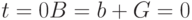 , при
, при 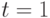 внешний спрос
внешний спрос  .
.
-