Моделирование структурными уравнениями

8.3. Моделирование структурными уравнениями и диаграммы путей

Диаграммы путей играют существенную роль в процессе структурного моделирования. Диаграммы путей напоминают блок-схемы и содержат переменные, связанные линиями, которые отображают причинные связи. Каждая связь, или путь, включает в себя две переменные (заключенные в прямоугольник или овал), соединенные стрелками (линиями, обычно прямыми, имеющими стрелку-указатель на одном конце) или дугами (линиями, обычно искривленными, без стрелок-указателей).

Путевые диаграммы наглядно показывают, какие переменные вызывают изменения в других переменных. Однако такое описание не является абсолютно точным. Возможно более точное описание.

Рассмотрим классическое линейное регрессионное уравнение 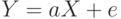. Его представление в виде пути показано на рис. 8.2.

Рис. 8.2.

Такие диаграммы устанавливают простое взаимно однозначное отображение, сохраняющее структуру модели, также называемое изоморфизмом. Все переменные в системе уравнений размещаются на диаграмме в прямоугольниках или овалах. Каждое уравнение отображается на диаграмме следующим образом. Все независимые переменные (из правой части уравнения) имеют стрелки, указывающие на зависимые переменные. Весовые коэффициенты располагаются вблизи от соответствующих стрелок. Снизу диаграмма содержит представление системы простых линейных уравнений в виде диаграммы путей.

Помимо представления линейных зависимостей в виде стрелок диаграмма содержит и некоторые другие элементы. Прежде всего это дисперсия независимых переменных, задаваемая для проверки модели структурных связей, которые на диаграмме отображаются изогнутыми линиями без стрелок. Такие линии называют дугами. Явные переменные, т.е. те, которые можно измерить непосредственно, на диаграммах указываются внутри прямоугольников. Латентные переменные, т.е. те, которые нельзя непосредственно измерить (например, факторы в факторном анализе или остатки в регрессионном), - внутри овалов или окружностей.

Например, переменная на диаграмме сверху (см. рис. 8.2) может рассматриваться как остаток линейной регрессии, когда значение предсказывается по значению . Такие остатки не наблюдаются непосредственно, но в принципе могут быть вычислены по известным значениям и (если a известно) и потому называются латентными (скрытыми) переменными и помещаются внутри овалов.

Конечно, рассмотренный пример диаграммы путей очень прост. Обычно требуется проверка намного более сложных моделей. Если система уравнений становится слишком сложной, как правило, переходят к рассмотрению ковариационных структур. В конечном счете модель может стать настолько сложной и запутанной, что уже невозможно понять ее основные принципы. Переменные могут быть связаны нелинейно или иметь линейную связь, не относящуюся к тому, что выбрано в качестве причины в модели. Например, навыки проверки причинных моделей слабо связаны с проверкой линейных моделей.

В общем, древнее изречение "наблюдаемая зависимость не означает причинной зависимости" остается верным даже для сложной и многомерной корреляции. Но вот что причинное моделирование действительно позволяет исследовать, так это степень отличия данных от соответствующих выводов причинной модели (а именно от предполагаемой ковариационной структуры). Если система линейных уравнений, изоморфная диаграмме путей, хорошо согласуется с данными, модель можно оставить для дальнейшего анализа или использования. Хотя это не доказывает ее истинность.

Диаграммы путей можно использовать для отражения причинных связей в наборе переменных, но они не предполагают реального наличия таких связей. Диаграммы путей часто используются для простого и изоморфного представления системы линейных уравнений. Значит, они могут выражать линейные связи независимо от того, имеются ли на самом деле описанные причинные связи. Следовательно, диаграмма (см. рис. 8.2), интерпретируемая нами как " влияет на ", также может обозначать графическое представление линейного регрессионного соотношения между и .

Контрольные вопросы

1. Для решения каких задач применяются методы структурного моделирования?
2. Нарисуйте блок-схему основных этапов структурного моделирования.
3. Объясните суть путевых диаграмм.
4. Какие переменные на диаграммах путей являются независимыми, а какие зависимыми?
5. Всегда ли построенные зависимости отражают реальные связи между переменными?