Задачи по разделам курса
Разбор снизу-вверх типа сдвиг- свертка
4.5.1. Построить все состояния для LR(0) -анализа грамматики G:

Будет ли G LR(0) -грамматикой? А LR(1)?
4.5.2. Является ли грамматика с правилами:
S -> A|B; B -> aB|b|C; A -> AA|a; C -> cC
LR(0) -грамматикой?
4.5.3. Сколько множеств LR(0) -ситуаций в канонической системе LR(0) -ситуаций грамматики G с правилами
а) S -> aA|aB A -> bA|c B -> bB|d; б) S -> A0|F1 A -> S0|B1 B -> A1|F0 F -> B0|S1; в) E -> (L)|a L -> EL|E.
4.5.4. Сколько LR(0) -таблиц имеет грамматика с правилами:
S -> Aa|Bb; B -> b; A -> ab.
4.5.5. Построить все состояния LR(1) -анализа для грамматики:
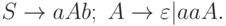
4.5.6. Сколько множеств LR(1) -ситуаций в канонической cистеме LR(1) -ситуаций грамматики G с правилами
а) S -> aSb|ab; б) S -> aAc|b A -> aSc|b.
4.5.7. Определить, является ли грамматика c приведенным набором правил LR(1) -грамматикой:
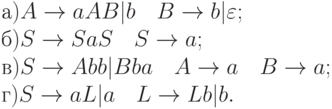
4.5.8. Построить все состояния анализа (K = 1) для грамматики
S -> S1; S1->S1S1; S1->a.
Будет ли эта грамматика LR(1)?
4.5.9. Построить все состояния LR(1) анализа для грамматики:
S -> aBc; B -> b; B -> bBb:
Применив критерий LR(K), определить, будет ли это LR(1) - грамматика.
4.5.10. Выяснить, являются ли следующие грамматики LR(k) -грамматиками. Найти точное значение k и построить детерминированный правый анализатор:
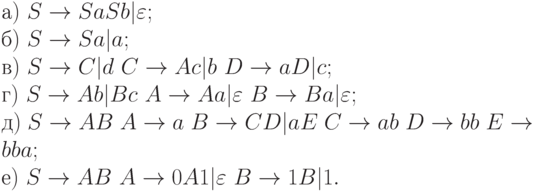
4.5.11. Является ли нижеприведенная грамматика LR(k), и если да, то определить минимальное k.
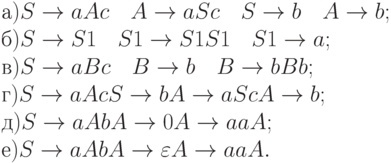
4.5.12. Являются ли следующие грамматики LR(k) - грамматиками? Указать точное значение k и построить соответствующий детерминированный правый анализатор.
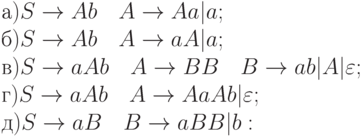
4.5.13. Для грамматики

написать эквивалентную LR(0) -грамматику.
4.5.14. Сколько сверток и переносов сделает LR(1) - анализатор для грамматики G = ({S, A}, {a}, P, S) c правилами S -> A A -> Aa|a при анализе цепочки a100?
4.5.15. Сколько SLR(1) -таблиц имеет грамматика с правилами:
S -> Aaa|Bb|C B -> aa A -> aa C -> cAc|cBd.
4.5.16. Сколько тактов сделает LALR(1) -анализатор для грамматики с правилами:
S -> A|BC B -> a A -> a; C -> AAAS при разборе цепочки aaaaa?
4.5.17. Выписать цепочку минимальной длины, на которой видны отличия LARL(1) и LR(1) -анализаторов для грамматики с правилами:
S -> Aa|Bb|C B -> aa A -> aa C -> cAc|cBd.
4.5.18. Пусть G = (N, T, P, S) - LR(1) -грамматика,  . В каких случаях (в зависимости от G и w ) LR(1) -
анализатор при анализе цепочки w не сделает ни одного
сдвига?
. В каких случаях (в зависимости от G и w ) LR(1) -
анализатор при анализе цепочки w не сделает ни одного
сдвига?
4.5.19. Пусть G = (N, T, P, S) - LR(1) -грамматика;  : Пусть k - число сдвигов, делаемых LR(1) -
анализатором при анализе цепочки w. Привести нижнюю и
верхнюю оценку для числа k.
: Пусть k - число сдвигов, делаемых LR(1) -
анализатором при анализе цепочки w. Привести нижнюю и
верхнюю оценку для числа k.
4.5.20. Пусть G = (N, T, P, S) - LR(1) -грамматика,  . Пусть k - число
сверток, делаемых LR(1) -анализатором при анализе цепочки w. Привести нижнюю оценку для числа k.
. Пусть k - число
сверток, делаемых LR(1) -анализатором при анализе цепочки w. Привести нижнюю оценку для числа k.
4.5.21. Пусть G = (N, T, P, S) - LR(1) -грамматика,  . Пусть k - число
сверток, делаемых LR(1) -анализатором при анализе цепочки w. Привести нижнюю оценку для числа k.
. Пусть k - число
сверток, делаемых LR(1) -анализатором при анализе цепочки w. Привести нижнюю оценку для числа k.
4.5.22. Существует ли LR(1) -грамматика, для которой функция действий LR(1) -таблицы не содержит элементов "ошибка" ?
4.5.23. Дана КС-грамматика G = (N, T, P, S). Найти верхнюю оценку числа LR(1) -ситуаций для G.
4.5.24. Дана LR(1) -грамматика без  -правил G и цепочка
-правил G и цепочка 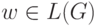 . В дереве разбора w - n1 листьев и n2 внутренних
вершин. Сколько сдвигов и сверток сделает LR(1) -анализатор
для G при анализе цепочки w?
. В дереве разбора w - n1 листьев и n2 внутренних
вершин. Сколько сдвигов и сверток сделает LR(1) -анализатор
для G при анализе цепочки w?

