Решение задач на динамические структуры данных
Деки
Дек является особым видом очереди.
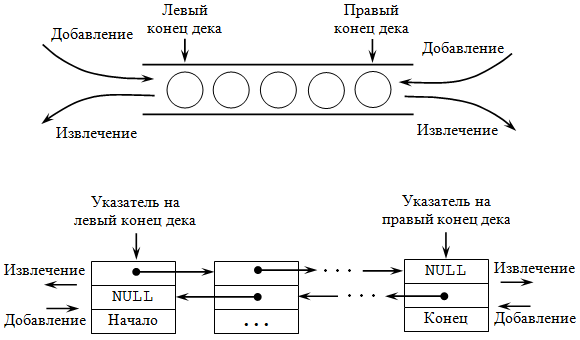
Дек (англ. deque – аббревиатура от double-ended queue, двухсторонняя очередь) – это структура данных, представляющая собой последовательность элементов, в которой можно добавлять и удалять в произвольном порядке элементы с двух сторон ( рис. 32.3). Первый и последний элементы дека соответствуют входу и выходу дека.
Частные случаи дека – это ограниченные деки:
- дек с ограниченным входом – из конца дека можно только извлекать элементы;
- дек с ограниченным выходом – в конец дека можно только добавлять элементы.
Данная структура является наиболее универсальной из рассмотренных выше линейных структур. Накладывая дополнительные ограничения на операции с началом и/или концом дека, можно осуществлять моделирование стека и очереди.
Однако применительно к деку целесообразно говорить не о начале и конце как в очереди, а о левом и правом конце.
Описание элементов дека аналогично описанию элементов линейного двунаправленного списка. Поэтому объявим дек через объявление линейного двунаправленного списка:
- создание дека;
- печать (просмотр) дека;
- добавление элемента в левый конец дека;
- добавление элемента в правый конец дека;
- извлечение элемента из левого конца дека;
- извлечение элемента из правого конца дека;
- проверка пустоты дека;
- очистка дека.
Реализацию этих операций приведем в виде соответствующих функций, которые, в свою очередь, используют функции операций с линейным двунаправленным списком.
//создание дека
void Make_Deque(int n, Deque* End_Deque){
Make_Double_List(n,&(End_Deque->Begin),NULL);
Double_List *ptr; //вспомогательный указатель
ptr = End_Deque->Begin;
while (ptr->Next != NULL){
ptr = ptr->Next;
}
End_Deque->End = ptr;
}
//печать дека
void Print_Deque(Deque* Begin_Deque){
Print_Double_List(Begin_Deque->Begin);
}
//добавление элемента в правый конец дека
void Add_Right_Item_Deque(int NewElem, Deque* End_Deque){
End_Deque->End =Insert_Item_Double_List(End_Deque->End,2,NewElem);
End_Deque->End = End_Deque->End->Next;
}
//добавление элемента в левый конец дека
void Add_Left_Item_Deque(int NewElem, Deque* Begin_Deque){
Begin_Deque->Begin =
Insert_Item_Double_List(Begin_Deque->Begin, 1, NewElem);
}
//извлечение элемента из левого конца дека
int Extract_Left_Item_Deque(Deque* Begin_Deque){
int NewElem = NULL;
if (Begin_Deque->Begin != NULL) {
NewElem = Begin_Deque->Begin->Data;
Begin_Deque->Begin=Delete_Item_Double_List(Begin_Deque->Begin,0);
//удаляем вершину
}
return NewElem;
}
//извлечение элемента из правого конца дека
int Extract_Right_Item_Deque(Deque* End_Deque){
int NewElem = NULL;
if (End_Deque->End != NULL) {
NewElem = End_Deque->End->Data;
Delete_Item_Double_List(End_Deque->End, 1);
//удаляем вершину
}
return NewElem;
}
//проверка пустоты очереди
bool Empty_Deque(Deque* Begin_Deque){
return Empty_Double_List(Begin_Deque->Begin);
}
//очистка очереди
void Clear_Deque(Deque* Begin_Deque){
Delete_Double_List(Begin_Deque->Begin);
}
Листинг
3.
Красно-черные деревья
Бинарные деревья работают лучше всего, когда они сбалансированы, когда длина пути от корня до любого из листьев находится в определенных пределах, связанных с числом вершин. Красно-черные деревья являются одним из способов балансировки деревьев. Название происходит от стандартной раскраски узлов таких деревьев в красный и черный цвета. Цвета вершин используются при балансировке дерева.
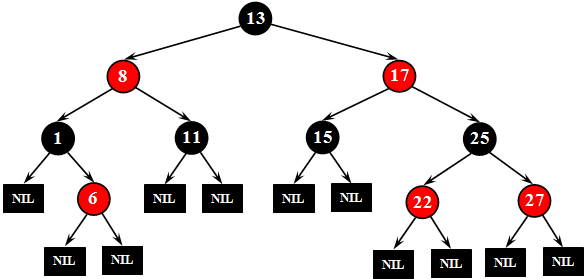
Красно-черное дерево ( Red-Black-Tree, RB-Tree ) – это бинарное дерево со следующими свойствами ( рис. 32.4):
- каждая вершина должна быть окрашена либо в черный, либо в красный цвет;
- корень дерева должен быть черным;
- листья дерева должны быть черными и объявляться как NIL-вершины (NIL-узлы, то есть "виртуальные" узлы, наследники узлов, которые обычно называют листьями; на них "указывают" NULL указатели);
- каждый красный узел должен иметь черного предка;
- на всех ветвях дерева, ведущих от его корня к листьям, число черных вершин одинаково.
Количество черных вершин на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства гарантируют, что самая длинная ветвь от корня к листу не более чем вдвое длиннее любой другой ветви от корня к листу.
Над красно-черными деревьями можно выполнять все те же основные операции, что и над бинарными деревьями.
Приведем функции следующих операций над красно-черными деревьями: создание дерева, печать (просмотр) дерева, обход дерева, проверка пустоты дерева и удаление дерева.
//создание красно-черного дерева
void Make_RBTree(RBTree** Node, int n){
int Data;
while (n > 0) {
cout << "Введите значение ";
cin >> Data;
Insert_Node(Node, Data);
n--;
}
}
//добавление узла в красно-черное дерево
void Insert_Node(RBTree** Node,int Data) {
RBTree **Curent, *Parent, *New_Node;
Curent = Node;
Parent = NIL;
// Поиск местоположения
while (*Curent != NIL) {
Parent = (*Curent);
Curent = Data < (*Curent)->Data ? &((*Curent)->Left) : &((*Curent)->Right);
}
// Создание нового узла
New_Node = new RBTree();
New_Node->Data = Data;
New_Node->Parent = Parent;
New_Node->Left = NIL;
New_Node->Right = NIL;
New_Node->color = RED;
// Вставка элемента в дерево
if(Parent != NIL){
if (Data < Parent->Data) Parent->Left = New_Node;
else Parent->Right = New_Node;
}
else (*Curent) = New_Node;
Insert_Fixup(Node, New_Node);
}
// Поддержка баланса дерева после вставки нового элемента
void Insert_Fixup(RBTree** Node,RBTree* New_Node){
RBTree* Current = New_Node;
// Проверка свойств дерева
while (Current != *(Node) && Current->Parent->color == RED){
// если есть нарушение
if (Current->Parent == Current->Parent->Parent->Left) {
RBTree *ptr = Current->Parent->Parent->Right;
if (ptr->color == RED) {
Current->Parent->color = BLACK;
ptr->color = BLACK;
Current->Parent->Parent->color = RED;
Current = Current->Parent->Parent;
}
else {
if (Current == Current->Parent->Right) {
// сделать Current левым потомком
Current = Current->Parent;
Rotate_Left(Node,Current);
}
// перекрасить и повернуть
Current->Parent->color = BLACK;
Current->Parent->Parent->color = RED;
Rotate_Right(Node,Current->Parent->Parent);
}
}
else {
RBTree *ptr = Current->Parent->Parent->Left;
if (ptr->color == RED) {
Current->Parent->color = BLACK;
ptr->color = BLACK;
Current->Parent->Parent->color = RED;
Current = Current->Parent->Parent;
}
else {
if (Current == Current->Parent->Left) {
Current = Current->Parent;
Rotate_Right(Node,Current);
}
Current->Parent->color = BLACK;
Current->Parent->Parent->color = RED;
Rotate_Left(Node,Current->Parent->Parent);
}
}
}
(*Node)->color = BLACK;
}
//поворот узла Current влево
void Rotate_Left(RBTree** Node,RBTree *Current) {
RBTree *ptr = Current->Right;
Current->Right = ptr->Left;
if (ptr->Left != NIL) ptr->Left->Parent = Current;
if (ptr != NIL) ptr->Parent = Current->Parent;
if (Current->Parent != NIL) {
if (Current == Current->Parent->Left)
Current->Parent->Left = ptr;
else
Current->Parent->Right = ptr;
}
else {
(*Node) = ptr;
}
ptr->Left = Current;
if (Current != NIL) Current->Parent = ptr;
}
//поворот узла Current вправо
void Rotate_Right(RBTree** Node,RBTree *Current) {
RBTree *ptr = Current->Left;
Current->Left = ptr->Right;
if (ptr->Right != NIL) ptr->Right->Parent = Current;
if (ptr != NIL) ptr->Parent = Current->Parent;
if (Current->Parent != NIL) {
if (Current == Current->Parent->Right)
Current->Parent->Right = ptr;
else
Current->Parent->Left = ptr;
}
else {
(*Node) = ptr;
}
ptr->Right = Current;
if (Current != NIL) Current->Parent = ptr;
}
//печать красно-черного дерева
void Print_RBTree(RBTree* Node, int l){
int i;
if (Node != NIL) {
Print_RBTree(Node->Right, l+1);
for (i=0; i< l; i++) cout << " ";
if (Node->color == RED)
SetConsoleTextAttribute(hStd,FOREGROUND_RED);
cprintf ("%4ld", Node->Data);
SetConsoleTextAttribute(hStd,atr);
Print_RBTree(Node->Left, l+1);
}
else cout << endl;
}
//прямой обход красно-черного дерева
void PreOrder_RBTree(RBTree* Node){
if (Node != NIL) {
printf ("%3ld",Node->Data);
PreOrder_RBTree(Node->Left);
PreOrder_RBTree(Node->Right);
}
}
//обратный обход красно-черного дерева
void PostOrder_RBTree(RBTree* Node){
if (Node != NIL) {
PostOrder_RBTree(Node->Left);
PostOrder_RBTree(Node->Right);
printf ("%3ld",Node->Data);
}
}
//симметричный обход красно-черного дерева
void SymmetricOrder_RBTree(RBTree* Node){
if (Node != NIL) {
PostOrder_RBTree(Node->Left);
printf ("%3ld",Node->Data);
PostOrder_RBTree(Node->Right);
}
}
//проверка пустоты красно-черного дерева
bool Empty_RBTree(RBTree* Node){
return ( Node == NIL ? true : false );
}
//освобождение памяти, выделенной под красно-черное дерево
void Delete_RBTree(RBTree* Node){
if (Node != NIL) {
Delete_RBTree(Node->Left);
Delete_RBTree(Node->Right);
delete(Node);
}
}
Листинг
4.
Ключевые термины
Циклический (кольцевой) список – это структура данных, представляющая собой последовательность элементов, последний элемент которой содержит указатель на первый элемент списка, а первый (в случае двунаправленного списка) – на последний.
Дек – это структура данных, представляющая собой последовательность элементов, в которой можно добавлять и удалять в произвольном порядке элементы с двух сторон.
Дек с ограниченным входом – это дек, из конца которого можно только извлекать элементы;
Дек с ограниченным выходом – это дек, в конец которого можно только добавлять элементы.
Красно-черное дерево (Red-Black-Tree, RB-Tree) – это бинарное дерево со следующими свойствами:
- каждая вершина должна быть окрашена либо в черный, либо в красный цвет;
- корень дерева должен быть черным;
- листья дерева должны быть черными и объявляться как NIL-вершины;
- каждый красный узел должен иметь черного предка;
- на всех ветвях дерева, ведущих от его корня к листьям, число черных вершин одинаково.
Черная высота дерева – это количество черных вершин на ветви красно-черного дерева от корня до листа.
Краткие итоги
- Особенности указателей в языке С++ позволяют строить динамические структуры памяти на основе статически объявленных переменных или на смеси статических и динамических переменных.
- Циклический (кольцевой) список является структурой данных, представляющей собой последовательность элементов, последний элемент которой содержит указатель на первый элемент списка, а первый (в случае двунаправленного списка) – на последний.
- Основными операциями с циклическим списком являются: создание списка; печать (просмотр) списка; вставка элемента в список; удаление элемента из списка; поиск элемента в списке; проверка пустоты списка; удаление списка.
- Дек является структурой данных, представляющей собой последовательность элементов, в которой можно добавлять и удалять в произвольном порядке элементы с двух сторон. Первый и последний элементы дека соответствуют входу и выходу дека.
- Частные случаи дека – это ограниченные деки.
- Основными операциями с деком являются: создание дека; печать (просмотр) дека; добавление элемента в левый конец дека; добавление элемента в правый конец дека; извлечение элемента из левого конца дека; извлечение элемента из правого конца дека; проверка пустоты дека; очистка дека.
- Красно-черные деревья являются одним из способов балансировки деревьев, что определяется свойствами данной структуры.
- Над красно-черными деревьями можно выполнять все те же основные операции, что и над бинарными деревьями.
- При вставке/удалении элемента необходима поддержка баланса дерева через проверку и перекрашивание узлов при необходимости.