Планирование развития региональной логистической системы
11.2. Целевое управление развитием системы транспортного обслуживания региона
Целевые методы предполагают конкретную технологию управления: формирование иерархии целей, образование взаимоувязанных программ, реализующих цели, распределение имеющихся ресурсов, формирование бюджета, создание (при необходимости) специальных органов управления.
В теории и практике социально-экономического управления определение главных целей и методы согласования целей разных уровней исследовано недостаточно. До сего времени нет правил, согласно которым разработчики, осуществляющие целеполагание по отношению к одному и тому же объекту, приходили бы к полному единству результатов. В этой связи формирование и уточнение целей, построение иерархии подцелей, доведение их до соответствующего уровня приоритетности главной цели по отношению к целям "низшего" уровня - одна из важнейших задач управления.
Процесс формирования целей развития системы транспортного обслуживания региона разделяется на три фазы:
- структуризация ("разложение") проблемных ситуаций на проблему и подпроблемы с целью раскрытия причин возникновения проблемной ситуации;
- формирование "дерева целей" развития СТОР, т.е. целей, направленных на решение региональных проблем транспортного обслуживания;
- постановка конкретных задач, направленных на достижение целей (как перспективных ориентиров развития), разработка вариантов достижения целей.
При целеполагании решаются три задачи: сокращение множества возникающих целей до минимума; выбор из минимума главной; исключение из "веера целей" тех, которые выступают как средство достижения других целей и не влияют на выбор.
Цель определяется по меньшей мере двумя методами. В первом случае она задается без предварительного анализа системы, определения ее возможностей. Часто под заданную цель заново создаются органы управления. Во втором случае цель выводится из состояния системы и выступает как ожидаемый к определенному времени результат (как будущее желаемое состояние системы). В обоих случаях анализируется состояние системы, оценка ее возможностей; в первом случае это делается с позиций заданной цели, а во втором - с позиций существующего состояния системы. Иначе говоря, с точки зрения необходимого уровня развития системы - первый случай; с точки зрения достигнутого уровня системы - второй случай.
После того как цель поставлена, возможности и ресурсы системы переоцениваются уже исходя из "интересов" цели. Учитываются и мобилизуются те из них, которые в наибольшей степени способствуют ее достижению. Достижение целей возможно только при соответствии их содержания объективным обстоятельствам. Отсюда следует, что степень достижения цели определяется характером такого соответствия. Это положение является ведущим методическим правилом в целеполагании.
Наиболее часто используемым методом целеполагания является формирование "дерева целей". Такая разработка осуществляется последовательной декомпозицией главной цели на подцели по определенным правилам. В результате образуется несколько уровней целей. Детализация целей возрастает по мере перехода от первого уровня к последующим.
Структуру целей типа "дерево" по степени детерминированности можно классифицировать следующим образом: со строго детерминированными уровнями - показатели любого уровня связаны с показателями только соседних уровней ( рис. 11.6а); со слабо детерминированными уровнями - показатели любого уровня связаны с показателями любых уровней ( рис. 11.6б); с недетерминированными уровнями - на каждом уровне расположен только один показатель ( рис. 11.6в).
Первые два вида графов могут иметь "свернутую" и "развернутую" структуры. В "развернутой" структуре каждый показатель связан только с одним показателем вышележащего уровня ( рис. 11.6а). Его "свернутая" структура представлена на рис. 11.6г.
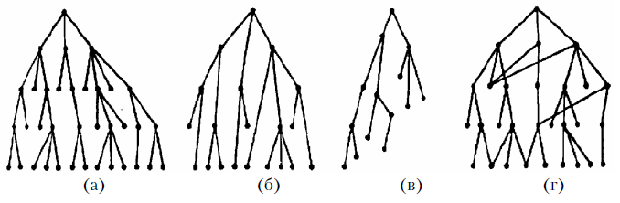
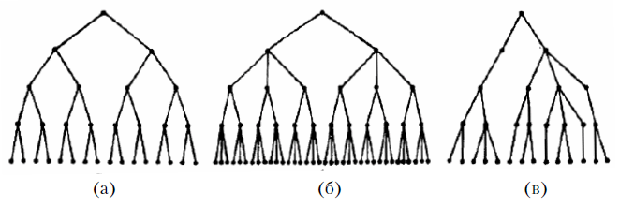
В зависимости от количества подчиненных вершин (показателей или целей) иерархические структуры по степени регулярности делятся на идеальные - число подчиненных вершин у всех невисячих вершин постоянно, т.е. невисячая вершина имеет подчиненные вершины ( рис. 11.7а), регулярные - число подчиненных вершин у всех вершин любого уровня постоянно ( рис. 11.7б) и нерегулярные - число вершин переменно от уровня к уровню и на уровне ( рис. 11.7в). Все вершины графа типа "дерево" взаимосвязаны.
"Дерево целей" имеет связи (ребра) вида "и" и "только". Наличие связи "и" означает, что вершина γ-го уровня связана не менее чем с двумя вершинами нижележащего (? + 1)-го уровня, причем при рассмотрении этой вершины необходимо анализировать все связанные с ней вершины (? + 1)-го уровня. Связь "только" показывает, что вершина ?-го уровня соединена только с одной вершиной (? + 1)-го уровня.
Рассмотрим различные графы-"деревья" с точки зрения удобства выполнения основных операций комплексной оценки целей развития транспортной системы региона. Анализ целей (γ + 1)-го уровня производится исходя из "требований" вышерасположенной цели.
Поэтому желательно, чтобы все цели ?-го уровня были связаны с целями (? - 1)-го уровня. Такая связь осуществляется "граф-деревом" со строго детерминированными уровнями. Если цели развития СТОР невозможно (или трудно) свести в "дерево" со строго детерминированными уровнями, можно использовать структуру со слабо детерминированными уровнями.
Важным требованием к "дереву" является его наглядность; это облегчает работу экспертов. В значительной степени наглядность обеспечивается непересечением ребер графа, т.е. применением "развернутой" структуры. Для этого в "развернутой" структуре цель нужно столько раз повторить, сколько связей она имела с вышележащими показателями в свернутой структуре ( рис. 11.6а).
Опыт работы с экспертами при целеполагании (построении "дерева целей") свидетельствует, что при определении коэффициентов весомости целей развития СТОР желательно иметь примерно одинаковым число показателей, определяющих каждую цель вышележащего уровня. Увеличение числа показателей может привести к снижению их коэффициентов весомости. В наибольшей степени действие неравного числа целей сказывается в случае, когда показатель качества повторяется на двух или более уровнях. Следовательно, целесообразно применять регулярную иерархическую структуру, при этом связи вида "только" нежелательны.
Из всех операций оценки целей развития СТОР построение структурной схемы в наименьшей степени поддается формализации и является сложной эвристической процедурой. Назначая коэффициенты весомости, эксперт сравнивает важность различных целей, входящих в однородную группу. При значительном числе целей эта операция становится затруднительной, что снижает точность оценок. Количество показателей определяется возможностями человека (эксперта) и используемым методом. Согласно важному положению экспериментальной психологии, человеку трудно одновременно работать более чем с 5-7 альтернативами, поэтому при использовании метода последовательных сравнений коэффициент весомости самого важного показателя принимается равным 1, а остальным приписываются меньшие значения. В этом случае количество показателей, входящих в группу, может быть увеличено до 8-10.
На последнем уровне "дерева целей" обычно располагаются единичные показатели, не разлагаемые на другие, более простые. Эти показатели могут быть измерены в натуральных единицах или баллах. Но некоторые комплексные показатели могут быть определены и расчетным методом с использованием функциональной зависимости между данными показателями и показателями более низких уровней. При построении структурной схемы целесообразно опускаться до такого уровня, на котором находятся цели (единичные и комплексные), значения которых могут быть определены любым из известных методов. Это позволит снизить трудоемкость и повысить точность выбора приоритетов развития СТОР при использовании экспертных методов. Количество единичных показателей зависит от сложности оцениваемого объекта.
Применяя расчетные формулы и точные исходные данные, можно получить точное решение. Но во многих случаях, связанных с неопределенностью ситуации, ее вероятностным характером, точных данных получить нельзя. Поэтому эвристическое решение эксперта (или группы экспертов) зачастую оказывается более правильным, чем решение, полученное расчетным путем с помощью математической формулы.
Таким образом, экспертные методы применяются тогда, когда использование других, более объективных методов оказывается невозможным и (или) неэкономичным. Применению экспертных методов способствует то обстоятельство, что в процессах управления зачастую нужны только определенные знания и только на определенный срок. В этих условиях нередко целесообразнее брать их "напрокат", используя экспертов со стороны.
Среди многочисленных разновидностей экспертных методов наибольшую известность получили два: Дельфи и ПАТТЕРН. Метод ПАТТЕРН назван по первым буквам английских слов, означающих "Помощь планированию посредством количественной оценки технических данных". Метод был разработан в 1962-1964 гг. американской фирмой "Хониуэлл" для оценки проектов новых систем вооружения (с точки зрения соответствия их национальным целям США). Кроме первого описания ПАТТЕРН, появившегося в 1964 г., известен и ряд других работ, посвященных этому методу. Однако общее их число значительно меньше количества работ, связанных с методом Дельфи. На русском языке имеется капитальная монография М.М. Лопухина. Одно из важных различий между обоими методами - способ опроса экспертов, и с этой точки зрения большинство остальных методов экспертной оценки могут рассматриваться как их модификации. В методе Дельфи отсутствует непосредственное общение между экспертами, в методе ПАТТЕРН такое общение является составным элементом процедуры их опроса. Подобное различие между двумя способами проведения опроса экспертов не является спецификой только методов Дельфи и ПАТТЕРН, оно было известно задолго до разработки этих методов. В качестве основного, наиболее опробованного и совершенного с методической точки зрения целесообразно использовать метод Дельфи.
Отличительная особенность метода Дельфи заключается в отказе от совместной работы экспертов, чтобы избежать конформизма, т.е. искажения действительного мнения эксперта под влиянием таких психологических факторов, как внушение или приспособление к мнению большинства других экспертов. Эксперт высказывает свое суждение не в ходе группового обсуждения, а излагаемого в анкете, снабженной подробной пояснительной запиской. Для получения дополнительной информации экспертам дают возможность ознакомиться с анонимными анкетами других экспертов, в результате чего во втором или последующих турах опроса они имеют право изменить первоначальную точку зрения.
В исходном варианте (при использовании для прогнозирования) метод Дельфи имел ряд недостатков, которые исследовались его авторами и другими специалистами. Главные из них: нестабильность состава экспертных групп, значительные разрывы во времени между турами, нечеткие формулировки вопросов, неучет компетентности экспертов, необоснованность выбранного метода усреднения экспертных оценок. При последующей работе часть недостатков удалось устранить. В результате появились разновидности этого метода: метод СИИР, Дельфи-ПЕРТ, модифицированный Дельфи и др. Были получены дополнительные доказательства теоретической корректности метода Дельфи применительно к задаче прогнозирования. Именно поэтому метод Дельфи в настоящее время стал наиболее широко применяемым инструментом прогнозирования.
Процесс прогнозной экспертизы обычно проводится в несколько туров.
На первом туре экспертам сообщается цель экспертизы и формируются вопросы, из которых и составляют основное содержание экспертизы. Вопросы предъявляются каждому эксперту персонально в виде анкеты, иногда сопровождаемой пояснительной запиской. Если предъявляемые экспертам вопросы достаточно сложны, целесообразна предварительная разработка приближенной модели исследуемой системы, чтобы правильно ориентировать эксперта, конкретизировать цели и предмет экспертной группы, показать характер возможных ответов.
Успеху экспертизы может способствовать предоставление эксперту дополнительной информации о предмете экспертизы. Информация, полученная от эксперта, поступает в распоряжение аналитической группы, обеспечивающей организацию, проведение, обработку промежуточных и окончательных результатов экспертизы. Аналитическая группа определяет экспертов, высказавших "крайние" точки зрения, давших самую высокую и самую низкую оценку альтернативе, усредненное мнение экспертов - медиану, верхнюю и нижнюю квартили, т.е. значение оцениваемой альтернативы, выше и ниже которых расположены 25% численности значений оценок. Расстояние между квартилями характеризует разброс экспертных оценок и характеризует согласованность точек зрения экспертов.
Вводятся следующие обозначения:
 |
- | значение наиболее ранней оценки; | |
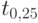 |
- | значение оценки, определяющей 25% наиболее ранних оценок (из всех имеющихся), - нижний квартиль; | |
 |
- | значение оценки, разделяющей упорядоченную по оси времени совокупность оценок на две равные по количеству оценок части - медиана; | |
 |
- | значение оценки, определяющей 25% наиболее поздних оценок (из всех имеющихся), - верхний квартиль; | |
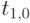 |
- | значение наиболее поздней оценки. |
Значение 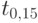 принимается за показатель обобщенного мнения экспертов об ожидаемом времени свершения определенного события.
принимается за показатель обобщенного мнения экспертов об ожидаемом времени свершения определенного события.
Степень согласованности мнений экспертов определяют коэффициентом вариации 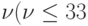 :
:
Медиана - значение признака, которое находится в середине ранжированного ряда. Для нахождения медианы ряда с четным числом вариант складывают две средние варианты и делят сумму пополам.
После этого (на втором этапе применения метода) экспертам предъявляется усредненная оценка экспертной комиссии и обоснования экспертов, высказавших "крайние" точки зрения. Обоснования принимаются анонимно, без указания имен экспертов. После получения дополнительной информации эксперты, как правило, корректируют свои оценки. Измененная информация вновь поступает в аналитическую группу.
Затем (на третьем этапе) эта информация вместе с анонимными аргументациями поставленных оценок снова направляется каждому участнику. Если оценка какого-либо эксперта значительно выходит за рамки общего интервала, то он должен подтвердить достаточной аргументацией свою позицию и объяснить, почему предыдущая информация и аргументация противоположных оценок не заставили его изменить свое мнение.
Далее (на четвертом этапе) каждый эксперт распределяет оценки третьего этапа и снова дает для анализа пересмотренную оценку с учетом полученной информации. Обычно желаемое согласие наступает к четвертому этапу. В некоторых случаях согласованная точка зрения экспертов может быть получена уже после второго или третьего этапов. Тогда необходимость проведения следующих этапов отпадает.
Для экономии расходов к прогнозированию стараются привлекать минимальное число экспертов. Минимальное число экспертов определяют по формуле
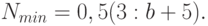 |
( 11.3) |
При этом должна наблюдаться стабилизация средней оценки прогнозируемой характеристики. О достижении этой стабилизации свидетельствует тот факт, что включение или исключение эксперта из группы не изменяет относительную оценку искомой величины более чем на b (0 < b < 1).
При использовании метода Дельфи следует учитывать, что:
- группы экспертов должны быть стабильными и их численность должна удерживаться в разумных рамках;
- время между турами опросов не должно превышать 30 дней;
- вопросы в анкетах должны быть тщательно продуманы и четко сформулированы;
- число туров должно быть достаточным, чтобы обеспечить всем участникам возможность ознакомиться с причиной той или иной оценки, а также и для анализа этих причин;
- должен проводиться систематический отбор экспертов;
- необходимо иметь самооценку компетенции экспертов по рассматриваемым проблемам;
- нужна формула согласованности оценок, основанная на самооценках;
- должно устанавливаться влияние общественного мнения на экспертные оценки и сходимость оценок;
- необходимо установить влияние различных видов передачи информации экспертам по каналам обратной связи.
Отметим, что использование меридианы и квартилей при методе Дельфи имеет не только достоинства, но и недостатки. В частности, при анализе результатов очередного тура оценка, чрезмерно отличающаяся от других, исключается, несмотря на то что может оказаться более верной, чем остальные (т.е. большинство экспертов могут сойтись в ошибочной оценке). Частично неправильное суждение компенсируется следующим. Эксперта, не согласного с большинством, просят высказать причины несогласия. Остальные эксперты имеют возможность не согласиться с его доводами или отвергнуть их, переоценить свое первоначальное мнение или сохранить. То есть оценка, существенно отличающаяся от других, отбрасывается фактически лишь в том случае, если эксперту не удается убедительно аргументировать свою точку зрения.
Имеется и другая трудность - сложно четко формулировать вопросы в анкетах. Максимальная точность нередко достигается громоздким стилем изложения, вызывающим отрицательную реакцию экспертов. Необходим оптимум между четкостью и лаконичностью поставленных вопросов, чтобы все участники их одинаково интерпретировали.
Третьим недостатком метода Дельфи является то, что ответы высококомпетентных экспертов "разбавляются" оценками менее информированных специалистов.
Эффективным целевым методом решения слабоструктурированных задач планирования и управления на различных уровнях экономической системы является метод анализа иерархий (МАИ). Этот метод состоит в декомпозиции проблемы на элементы, которые оцениваются по специальной шкале в виде суждений. После обработки суждений методами матричной алгебры формируются конечные оценки и определяется степень взаимного влияния элементов "дерева".
Иерархия всегда строится с вершины (целей - с точки зрения управления), через промежуточные уровни (критерии, от которых зависят последующие уровни) к самому низкому уровню (который обычно является перечнем альтернатив). Число уровней иерархии, описывающих конкретную задачу, может быть различно и зависит от специфики задачи. Каждый элемент верхнего уровня является "направляющим" для элементов нижнего уровня иерархии (это означает, например, важность); весовой коэффициент факторов описываемой альтернативы рассматривается относительно цели выбора альтернатив. Поэтому при бинарном сравнении факторов лицо, принимающее решение (ЛПР), оценивает каждый из них относительно поставленной цели выбора и соответственно определяет уровни взаимного предпочтения.
Проведя попарные сравнения на каждом из уровней иерархии, в конечном итоге получают вектора приоритетов для каждого уровня, степень влияния показателя нижнего уровня иерархии на показатель верхнего уровня (например, как изменение материально-технической базы повлияет на состояние грузовых или пассажирских перевозок и состояние всей СТОР).
Для нахождения векторов приоритетов формируют матрицы попарных сравнений для показателей каждого уровня иерархии, не являющегося верхним. Затем путем преобразований матриц определяется вектор приоритетов для каждого уровня. Все матрицы попарных сравнений должны быть согласованными. Для определения согласованности находится наибольшее собственное значение матрицы ( ), индекс согласованности (ИС) и отношение согласованности (ОС). Чем ближе значение
), индекс согласованности (ИС) и отношение согласованности (ОС). Чем ближе значение  к n, тем более согласованным является представление в матрице М[n] суждений ЛПР. Отклонение от согласованности может быть выражено индексом согласованности.
к n, тем более согласованным является представление в матрице М[n] суждений ЛПР. Отклонение от согласованности может быть выражено индексом согласованности.
Индекс согласованности рассчитывается по формуле
Для оценивания отношения согласованности используется отношение величины индекса согласованности к величине среднего случайного индекса (СИ), полученного методом имитационного моделирования для матрицы суждений того же порядка:
Значение 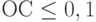 считается приемлемым порогом допустимой согласованности суждений. Если матрица не согласована, необходимо изменить оценки взаимных предпочтений в матрицах попарных сравнений.
считается приемлемым порогом допустимой согласованности суждений. Если матрица не согласована, необходимо изменить оценки взаимных предпочтений в матрицах попарных сравнений.
Получение оценки приоритетов направлений развития системы транспортного обслуживания региона дает возможность ЛПР количественно определить степень влияния того или иного фактора на состояние всей СТОР. Это позволяет, имея данные о фактических показателях состояния СТОР (протяженность железных дорог, количество перевезенных пассажиров, инвестиции в основные фонды транспорта и т.д.) и меняя их значение, достичь желаемого состояния СТОР в будущем периоде. Количественная оценка приоритетов развития системы транспортного обслуживания региона может служить основой для выбора направлений ее развития.
С помощью этой модели можно уточнить цели и направления развития СТОР, нормативно прогнозировать ее развитие в зависимости от целей развития экономики региона (например, количественно заданным процентом увеличения ВРП). При этом механизм прогноза может быть следующим. Устанавливается значение ВРП, которое необходимо достичь к определенному времени. Исходя из этого определяется значение интегрального показателя состояния системы транспортного обслуживания региона (ССТОР). Затем анализируются различные варианты (комбинации) значений расчетных показателей, используемых при определении ССТОР. На последнем этапе разрабатываются направления развития СТОР, приводящие к желаемым результатам. Каждое направление может быть оценено с точки зрения необходимых ресурсов и ожидаемых результатов.
Особенностью подготовки решений, касающихся достижения целей, отнесенных к категории альтернативных, является рассмотрение одновременно нескольких целей. Степень достижения каждой из них оценивается собственным показателем. Региональная администрация рассматривает возможные варианты действий, при которых одни цели достигаются в большей, другие - в меньшей степени.
Так как в "дереве" цели не взаимоисключающие, а дополняющие, для выбора наиболее приоритетного направления из трех элементов 2-го уровня и 8 элементов 3-го уровня в рассматриваемом ниже примере применен метод анализа иерархий.
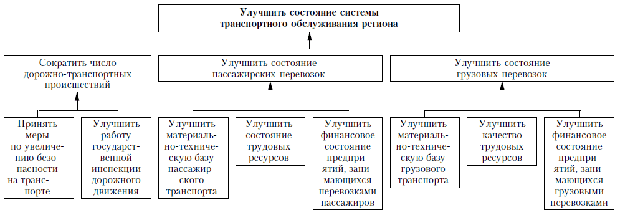
Фрагмент "дерева целей" развития системы транспортного обслуживания региона представлен на рис. 11.8.
увеличить изображение
Рис. 11.8. Фрагмент «дерева целей» развития системы транспортного обслуживания региона
Составим матрицы попарных сравнений, определим их согласованность и векторы приоритетов для каждого уровня иерархии в "дереве целей". Расчеты можно выполнять в табличном редакторе Excel-97. Итоговые результаты представлены в табл. 11.1-11.4.
| МАТРИЦА ПОПАРНЫХ СРАВНЕНИЙ | Состояние транспортной системы | Состояние грузовых перевозок | Состояние пассажирских перевозок | Число дорожно-транспортных происшествий |
|---|---|---|---|---|
| Состояние грузовых перевозок | 1 | 3 | 5 | |
| Состояние пассажирских перевозок | 0,333 | 1 | 3 | |
| Число дорожно-транспортных происшествий | 0,2 | 0,333 | 1 | |
| Вектор приоритетов | 0,6054 | 0,2915 | 0,1031 | |
Наибольшее собственное значение матрицы (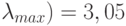
| ||||
| Индекс согласованности = 0,027 | ||||
| Отношение согласованности = 0,030 | ||||
| МАТРИЦА ПОПАРНЫХ СРАВНЕНИЙ | Состояние грузовых перевозок | Материально-техническая база | Состояние трудовых ресурсов | Финансовое состояние перевозчиков |
|---|---|---|---|---|
| Материально-техническая база | 1 | 5 | 3 | |
| Состояние трудовых ресурсов | 0,2 | 1 | 0,667 | |
| Финансовое состояние перевозчиков | 0,333 | 1,667 | 1 | |
| Вектор приоритетов | 0,6490 | 0,1346 | 0,2163 | |
Наибольшее собственное значение матрицы (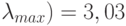
| ||||
| Индекс согласованности = 0,018 | ||||
| Отношение согласованности = 0,020 | ||||
| МАТРИЦА ПОПАРНЫХ СРАВНЕНИЙ | Состояние пассажирских перевозок | Материально-техническая база | Состояние трудовых ресурсов | Финансовое состояние перевозчиков |
|---|---|---|---|---|
| Материально-техническая база | 1 | 4 | 2 | |
| Состояние трудовых ресурсов | 0,25 | 1 | 0,333 | |
| Финансовое состояние перевозчиков | 0,5 | 3 | 1 | |
| Вектор приоритетов | 0,5360 | 0,1210 | 0,3439 | |
Наибольшее собственное значение матрицы (
| ||||
| Индекс согласованности = 0,013 | ||||
| Отношение согласованности = 0,014 | ||||
| МАТРИЦА ПОПАРНЫХ СРАВНЕНИЙ | Число дорожно-транспортных происшествий | Меры по увеличению безопасности на транспорте | Работа государственной инспекции дорожного движения |
|---|---|---|---|
| Меры по увеличению безопасности на транспорте | 1 | 2 | |
| Работа государственной инспекции дорожного движения | 0,5 | 1 | |
| Вектор приоритетов | 0,667 | 0,333 | |
Наибольшее собственное значение матрицы (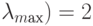
| |||
| Индекс согласованности = 0 | |||
| Отношение согласованности = 0 | |||
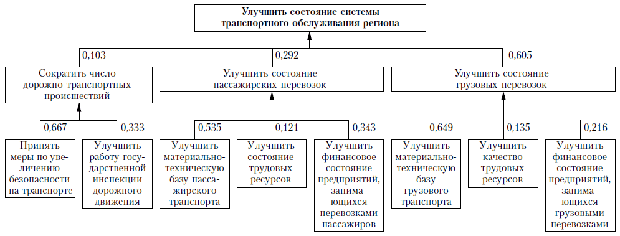
Таким образом получим оценку приоритетов по каждому уровню иерархии ( рис. 11.9).
Получение количественных оценок приоритетных направлений развития транспортной системы региона позволяет ЛПР численно определить степень влияния того или иного фактора на состояние всей СТОР. Имея данные о фактических показателях состояния СТОР (протяженность железных дорог, количество перевезенных пассажиров, инвестиции в основные фонды транспорта и т.д.) и изменяя (упреждая) их значение, можно достичь желаемого состояния ТСР в будущем периоде.
Серьезная проблема, которая встает перед исследователями, заключается в необходимости разработки методов количественного определения целей развития СТОР. Проблема усложняется, когда ее рассматривают применительно к отдельному федеральному округу, экономическому району, области, городу, т.е. когда приходится учитывать неравномерность развития регионов и их специфику. Возможный подход к решению этой проблемы - создание целевых нормативов: натуральных и условно-натуральных показателей, числовые значения которых показывают желаемый уровень транспортного обслуживания региональной экономики, определяемый по рациональным нормам, с помощью эталонов или посредством экспертных оценок.
Состояние и перспективы развития системы транспортного обслуживания региона могут отражать разные количественные и качественные показатели (грузооборот и пассажирооборот транспорта, плотность путей сообщения, протяженность автомобильных дорог с твердым покрытием, инвестиции в основной капитал транспорта). Их количество может быть значительным. Такие показатели могут сводиться в несколько блоков (около 10): пассажирские перевозки, грузовые перевозки, материально-техническая база, состояние трудовых ресурсов и другие. Выявление таких блоков само по себе уже представляет важный элемент структуризации факторов, отражающих состояние СТОР. Но сравнение различных регионов даже по небольшому числу показателей методически сложно. Поэтому заманчивым представляется применение единого, синтетического показателя, который может быть индикатором развития СТОР и использоваться в межрегиональных сравнениях. Этот показатель должен быть относительно прост в интерпретации, быть пригодным для прогнозирования и отражать взаимосвязь системы транспортного обслуживания с основными социально-экономическими показателями региона. Для этого необходимо иметь не только количественные значения интегрального показателя, но и модель его взаимосвязи с основными показателями, отражающими состояние социально-экономической системы региона. В качестве одного из последних, причем в модели, он станет результативным, можно взять, например, уровень социального развития (УСР) региона. Улучшение (рост значения) такого показателя может быть целевым, т.е. находиться на вершине "дерева целей" развития региона ( рис. 11.10).
В качестве интегрального показателя, отражающего состояние системы транспортного обслуживания региона, можно принять показатель состояния системы транспортного обслуживания региона (ССТОР). При его построении должны учитываться два момента: первый - теоретического характера - заключается в определении его составляющих и отборе первичных (измеряемых) признаков, второй - методического плана - нахождение методов сведения различных признаков (по характеру, единицам измерения) в единый интегральный показатель.
За показатели "дерева" примем: число дорожно-транспортных происшествий (ЧДТП); объем пассажирских перевозок (ОПП); объем грузовых перевозок (ОГП). Значения коэффициентов при показателях определим на основе метода анализа иерархии, рассчитав показатели относительной важности. При этом будем учитывать следующее обстоятельство: если увеличение значения показателя xi желательно, то коэффициент-параметр при показателе записываем со знаком "плюс", если нежелательно - со знаком "минус".
Исследование на статистических данных о ССТОР Курской области выявило, что интегральный показатель выглядит так:
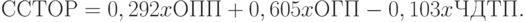 |
( 11.6) |
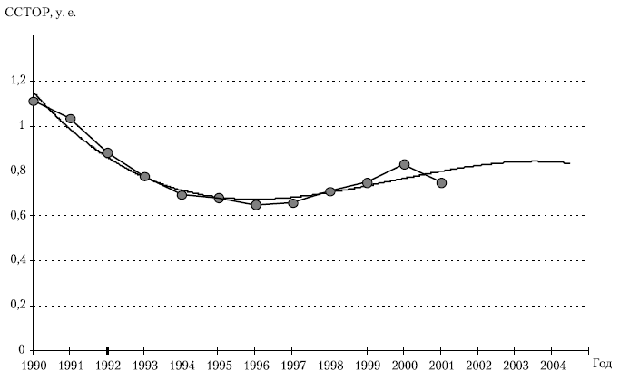
При сохранении прошлых тенденций в развитии показателей, составляющих интегральный показатель ССТОР, можно получить его генетический прогноз ( рис. 11.11).
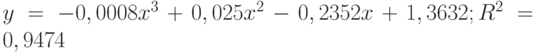
Результаты прогноза показывают, что к 2005 г. в системе транспортного обслуживания региона намечается спад, который может негативно отразиться на состоянии всей экономики региона, в частности, сказаться на снижении уровня валового регионального продукта. Поэтому возникает вопрос о корректировке развития СТОР для избегания неблагоприятных последствий. Корректирующие воздействия должны не только приводить к улучшению состояния СТОР, но и способствовать развитию всей региональной системы. Поэтому необходимо иметь модель, отражающую влияние развития СТОР на экономику. В качестве последней может быть предложена взаимосвязь интегрального показателя ССТОР и ВРП.
Применим модель зависимости валового регионального продукта (ВРП) от СТОР, т.е. предположим существование функции
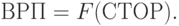 |
( 11.7) |
Путем многошаговой регрессии с использованием ресурсов табличного процессора Excel-97 получена следующая зависимость:
 |
( 11.8) |
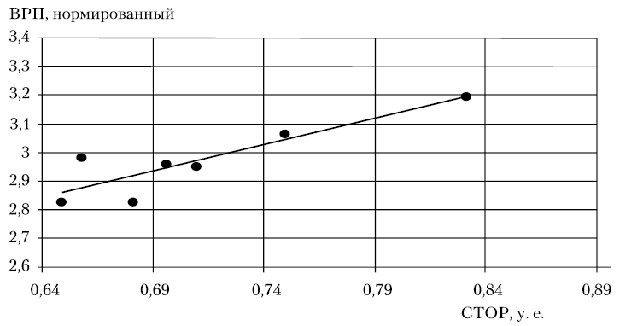
Количественное влияние ССТОР на ВРП определим по значению коэффициента эластичности 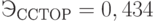 . Следовательно, при изменении величины ССТОР на 1% величина ВРП изменится на 0,434%. Графически модель представлена на
рис.
11.12.
. Следовательно, при изменении величины ССТОР на 1% величина ВРП изменится на 0,434%. Графически модель представлена на
рис.
11.12.
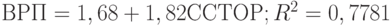




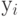
 .
. .
.