|
Хотела записаться на курс, но почему-то на сайте написано, что нужно приобрести его за 490 рублей. |
Использование функций
Статистические вычисления
О статистических функциях
Статистические функции используют при анализе данных. Использование большинства функций этой категории требует знания математической статистики и теории вероятностей. Всего в данной категории имеется 98 функций.
Расчет средних значений
В самом простом случае для расчета среднего арифметического значения используют функцию СРЗНАЧ.
СРЗНАЧ(А) ,
где А - список от 1 до 30 элементов, среднее значение которых требуется найти. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.
Если в диапазон, для которого рассчитывают среднее значение, попадают данные, существенно отличающиеся от остальных, расчет простого среднего арифметического может привести к неправильным выводам. В этом случае следует использовать функцию УРЕЗСРЕДНЕЕ. Эта функция вычисляет среднее, отбрасывая заданный процент данных с экстремальными значениями.
УРЕЗСРЕДНЕЕ(А;В) ,
где А - список от 1 до 30 элементов, среднее значение которых требуется найти. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются;
В - доля данных, исключаемых из вычислений.
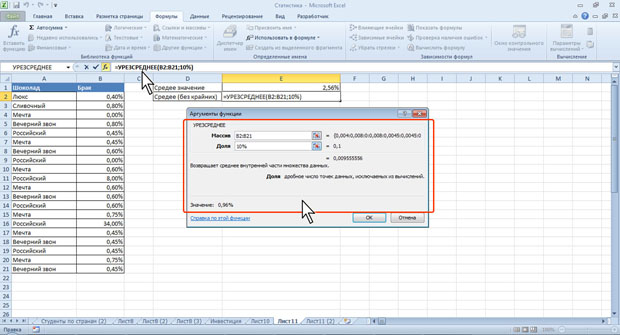
Доля данных, исключаемых из вычислений, указывается в процентах от общего числа данных. Например, доля 10 % означает, что из данных, содержащих 20 значений, отбрасываются 2 значения: одно наибольшее, другое - наименьшее. В таблице на рис.7.10 величина брака по одному из товаров (34 %) существенно отличается от остальных значений (8% и 34 %). Среднее арифметическое значение данных составляет 2,56 % (ячейка Е1 ), что дает несколько искаженную картину реальных значений. Расчет среднего значения с использованием функции УРЕЗСРЕДНЕЕ (ячейка Е2 ) дает более правильное представление о средних величинах брака в партиях товаров (0,96 %).
увеличить изображение
Рис. 7.10. Расчет среднего значения с отбрасыванием заданного процента данных с экстремальными значениями
При расчете средних темпов изменения какого-либо параметра более верное представление дает не среднее арифметическое, а среднее геометрическое значение. Особенно удобно пользоваться средним геометрическим значением при расчете средних темпов роста производства, среднего процента по вкладу и т. д. Для расчета среднего геометрического значения используют функцию СРГЕОМ.
СРГЕОМ(А) ,
где А - список от 1 до 30 элементов, среднее геометрическое значение которых требуется найти. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.
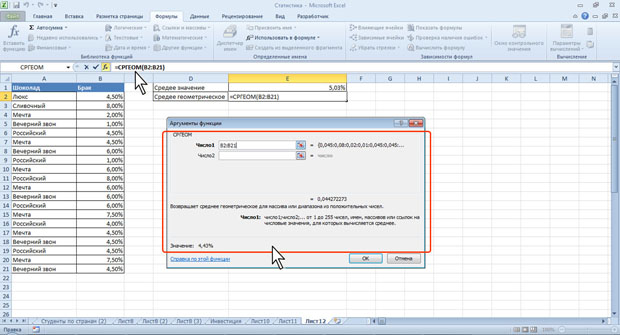
Например, для данных таблицы на рис.7.11 средний прирост реализации (среднее геометрическое) составит 3,46 % (ячейка Е3 ), в то время как среднее значение 4,33 % (ячейка Е2 ).
Нахождение крайних значений
Для нахождения крайних (наибольшего или наименьшего) значений в диапазоне данных используют функции МАКС и МИН.
МАКС(А) ,
где А - список от 1 до 30 элементов, среди которых требуется найти наибольшее значение. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.
Функция МИН имеет такой же синтаксис, что и функция МАКС.
Функции МАКС и МИН только определяют крайние значения, но не показывают, в какой ячейке эти значения находятся.
В тех случаях, когда требуется найти не самое большое (самое маленькое) значение, а значение, занимающее определенное положение в диапазоне данных (например, второе или третье по величине), следует использовать функции НАИБОЛЬШИЙ или НАИМЕНЬШИЙ.
НАИБОЛЬШИЙ(А; В),
где А - список от 1 до 30 элементов, среди которых требуется найти значение. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются;
В - позиция (начиная с наибольшей) в множестве данных. Если требуется найти второе значение по величине, то указывается позиция 2, если третье, то позиция 3 и т. д.
Функция НАИМЕНЬШИЙ имеет такой же синтаксис, что и функция НАИБОЛЬШИЙ.
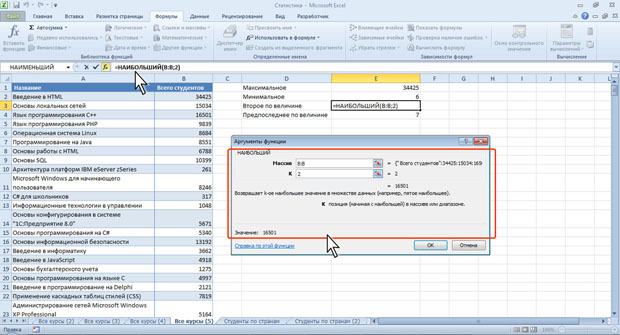
Например, для данных таблицы на рис.7.12 второе по величине значение составит 16501, а второе из наименьших - 7.