| Россия, Пошатово |
Контекстно-свободные грамматики
15.3.4. Написать LL(1)-грамматику для того же языка.
Решение.
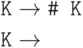
Как говорят, "леворекурсивное" правило заменено на "праворекурсивное".
Следующая задача показывает, что для LL(1)-грамматики существует не более одного возможного продолжения левого вывода.
15.3.5.
Пусть дано выводимое в LL(1)-грамматике слово  ,
в котором выделен самый левый нетерминал
,
в котором выделен самый левый нетерминал  :
: 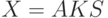 , где
, где  - слово из терминалов,
- слово из терминалов,  - слово из терминалов и нетерминалов. Пусть существуют два различных правила грамматики с нетерминалом
- слово из терминалов и нетерминалов. Пусть существуют два различных правила грамматики с нетерминалом  в левой части, и мы применили их к выделенному в
в левой части, и мы применили их к выделенному в  нетерминалу
нетерминалу  , затем продолжили
вывод и в конце концов получили два слова из терминалов,
начинающихся на
, затем продолжили
вывод и в конце концов получили два слова из терминалов,
начинающихся на  . Доказать, что в этих словах за
началом
. Доказать, что в этих словах за
началом  идут разные буквы. (Здесь к числу букв мы
относим EOI.)
идут разные буквы. (Здесь к числу букв мы
относим EOI.)
Решение. Эти буквы принадлежат направляющим множествам различных правил.
15.3.6. Доказать, что если слово выводимо в LL(1)-грамматике, то его левый вывод единствен.
Решение. Предыдущая задача показывает, что на каждом шаге левый вывод продолжается однозначно.
15.3.7.
Грамматика называется леворекурсивной, если из некоторого нетерминала  выводится слово, начинающееся с
выводится слово, начинающееся с  , но не совпадающее с ним. Доказать, что леворекурсивная грамматика, в которой из каждого нетерминала выводится хотя бы одно непустое слово из терминалов и для каждого нетерминала существует вывод (начинающийся с начального нетерминала), в котором он встречается, не является LL(1)-грамматикой.
, но не совпадающее с ним. Доказать, что леворекурсивная грамматика, в которой из каждого нетерминала выводится хотя бы одно непустое слово из терминалов и для каждого нетерминала существует вывод (начинающийся с начального нетерминала), в котором он встречается, не является LL(1)-грамматикой.
Решение. Пусть из  выводится
выводится 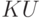 , где
, где  - нетерминал, а
- нетерминал, а  - непустое слово. Можно считать, что это левый
вывод (другие нетерминалы можно не заменять). Рассмотрим вывод
- непустое слово. Можно считать, что это левый
вывод (другие нетерминалы можно не заменять). Рассмотрим вывод
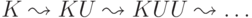
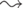 обозначает несколько шагов
вывода) и левый вывод
обозначает несколько шагов
вывода) и левый вывод  , где
, где  - непустое слово из терминалов. На каком-то шаге второй вывод отклоняется от первого, а между тем по обоим путям может быть получено слово, начинающееся на
- непустое слово из терминалов. На каком-то шаге второй вывод отклоняется от первого, а между тем по обоим путям может быть получено слово, начинающееся на  (в первом случае это возможно, так как сохраняется нетерминал
(в первом случае это возможно, так как сохраняется нетерминал  , который может впоследствии быть заменен на
, который может впоследствии быть заменен на  ). Это противоречит возможности однозначного определения правила, применяемого на очередном шаге поиска левого вывода. (Однозначность выполняется для выводов из начального нетерминала, и надо воспользоваться тем, что
). Это противоречит возможности однозначного определения правила, применяемого на очередном шаге поиска левого вывода. (Однозначность выполняется для выводов из начального нетерминала, и надо воспользоваться тем, что  по предположению встречается в таком выводе.)
по предположению встречается в таком выводе.)Таким образом, к леворекурсивным грамматикам (кроме тривиальных случаев) LL(1)-метод неприменим. Их приходится преобразовывать к эквивалентным LL(1)-грамматикам - или пользоваться другими методами распознавания.
15.3.8. Используя сказанное, построить алгоритм проверки выводимости слова из терминалов в LL(1)-грамматике.
Решение. Мы следуем описанному выше методу поиска левого вывода, храня лишь часть слова, находящуюся правее уже прочитанной части входного слова. Другими словами, мы храним слово S из терминалов и нетерминалов, обладающее такими свойствами (прочитанную часть входа обозначаем через A ):
Эти свойства вместе будем обозначать "(И)".
Вначале A пусто, а S состоит из единственного символа - начального нетерминала.
Если в некоторый момент S начинается на
терминал t и  , то
можно выполнить команду Move и удалить символ t,
являющийся начальным в S, поскольку при этом AS не
меняется.
, то
можно выполнить команду Move и удалить символ t,
являющийся начальным в S, поскольку при этом AS не
меняется.
Если S начинается на терминал t и  , то входное слово
невыводимо - ибо по условию любой его вывод должен проходить через AS. (Это же справедливо и в случае
, то входное слово
невыводимо - ибо по условию любой его вывод должен проходить через AS. (Это же справедливо и в случае 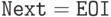 .)
.)
Если S пусто, то из условия (И) следует, что входное слово
выводимо тогда и только тогда, когда 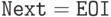 .
.
Остается случай, когда S начинается с некоторого нетерминала K. По доказанному выше все левые выводы из S слов, начинающихся на символ Next, начинаются с применения к S одного и того же правила - того, для которого Next принадлежит направляющему множеству. Если таких правил нет, то входное слово невыводимо. Если такое правило есть, то нужно применить его к первому символу слова S - при этом свойство (И) не нарушится. Приходим к такому алгоритму:
s := пустое слово;
error := false;
{error => входное слово невыводимо;}
{not error => (И)}
while (not error) and not ((Next=EOI) and (S пусто))
| | do begin
| if (S начинается на терминал, равный Next) then begin
| | Move; удалить из S первый символ;
| end else if (S начинается на терминал, не равный Next)
| | then begin
| | error := true;
| end else if (S пусто) and (Next <> EOI) then begin
| | error := true;
| end else if (S начинается на нетерминал и Next входит в
| | направляющее множество одного из правил для этого
| | нетерминала) then begin
| | применить это правило
| end else if (S начинается на нетерминал и Next не входит
| | в направляющее множество ни одного из правил для этого
| | нетерминала) then begin
| | error := true;
| end else begin
| | {так не бывает}
| end;
end;
{входное слово выводимо <=> not error}Алгоритм заканчивает работу, поскольку при появлении терминала в начале слова S происходит чтение со входа или остановка, а бесконечный цикл сменяющих друг друга нетерминалов в начале S означал бы, что грамматика леворекурсивна. (А мы можем предполагать, согласно предыдущей задаче, что это не так: нетерминалы, не встречающиеся в выводах, а также нетерминалы, из которых не выводится непустого слова, несложно удалить из грамматики.)
Замечания.
- Приведенный алгоритм использует S как стек (все действия производятся с левого конца).
- Действия двух последних вариантов внутри цикла не приводят к чтению очередного символа со входа, поэтому их можно заранее предвычислить для каждого нетерминала и каждого символа Next. После этого на каждом шаге цикла будет читаться очередной символ входа.
- При практической реализации удобно составить таблицу, в которой записаны варианты действий в зависимости от входного символа и первого символа S, и небольшую программу, выполняющую действия в соответствии с этой таблицей.
15.3.9.
При проверке того, относится ли данная грамматика к типу LL(1),
необходимо вычислить  и
и  для всех нетерминалов
для всех нетерминалов  .
Как это сделать?
.
Как это сделать?
Решение.Пусть, например, в грамматике есть правило 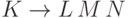 . Тогда
. Тогда

 ), а затем и Послед(
), а затем и Послед(  ), для всех терминалов и нетерминалов
), для всех терминалов и нетерминалов  .
При этом началом служит
.
При этом началом служит
 и
и
 . Порождение заканчивается, когда применение правил перестает давать новые элементы множеств Нач(T) и Послед(T).
. Порождение заканчивается, когда применение правил перестает давать новые элементы множеств Нач(T) и Послед(T).