| Россия, Пошатово |
Анализ игр
11.4. Альфа-бета-процедура
Мы видели, как можно вычислить цену игры, обойдя все вершины ее дерева. Однако иногда можно сэкономить и часть дерева не посещать. Пусть, например, игра имеет два исхода (выигрыш и проигрыш) и мы обнаружили (после просмотра части дерева), что некоторый ход является для нас выигрышным. Тогда нет смысла рассматривать остальные ходы. Более общо, если мы нашли ход, гарантирующий нам максимальный выигрыш (допускаемый правилами игры), то нет смысла искать дальше.
Подобная оптимизация возможна не только в тех случаях,
когда мы знаем максимально возможный выигрыш. Пусть,
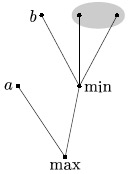
например, дерево игры имеет такой вид, как на
рис. 11.6, причем  и мы обходим вершины
дерева слева направо.
и мы обходим вершины
дерева слева направо.
 мы знаем, что цена
корневой вершины не меньше
мы знаем, что цена
корневой вершины не меньше  . Перейдя к min-вершине
и просмотрев ее первого сына
. Перейдя к min-вершине
и просмотрев ее первого сына  , мы определяем, что цена
min-вершины не больше
, мы определяем, что цена
min-вершины не больше  и (при
и (при  ) она не может
повлиять на цену корня. Поэтому следующие вершины (серая
область на рисунке) и их поддеревья нам просматривать не
нужно.
) она не может
повлиять на цену корня. Поэтому следующие вершины (серая
область на рисунке) и их поддеревья нам просматривать не
нужно.Примененную в обоих случаях оптимизацию можно описать так.
Приступая к оценке некоторой вершины, мы знаем некоторый
промежуток ![[m,M]](/sites/default/files/tex_cache/ba6b57aa9a15f2ee4db420cc0f475d7b.png) , в пределах которого нас интересует цена
этой вершины - либо потому, что она заведомо не может выйти
за пределы промежутка (как в первом случае, когда лучше
выигрыша ничего не бывает), либо потому, что это нам ничего
не дает (как во втором случае, когда все цены меньше
, в пределах которого нас интересует цена
этой вершины - либо потому, что она заведомо не может выйти
за пределы промежутка (как в первом случае, когда лучше
выигрыша ничего не бывает), либо потому, что это нам ничего
не дает (как во втором случае, когда все цены меньше  для нас неотличимы от
для нас неотличимы от  ).
).
Более формально, введем обозначение ![x_{[a,b]}](/sites/default/files/tex_cache/1d6844c596bf6cdc52e70775b4bb299b.png) , где
, где  -
число, а
-
число, а ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) - промежуток:
- промежуток:
![$$
x_{[a,b]}=\begin{cases}
a, &\text{если $x\le a$;}\\
x, &\text{если $a\le x\le b$;}\\
b, &\text{если $b\le x$.}
\end{cases}
$$](/sites/default/files/tex_cache/9ea34f6b40627b107bfed461c61e5693.png)
![x_{[a,b]}](/sites/default/files/tex_cache/1d6844c596bf6cdc52e70775b4bb299b.png) - ближайшая к
- ближайшая к  точка
промежутка
точка
промежутка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , которую можно назвать "приведенным
к
, которую можно назвать "приведенным
к ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) значением
значением  ". Теперь можно сказать, что
после
просмотра вершины
". Теперь можно сказать, что
после
просмотра вершины  на рисунке 11.6. нас
интересует приведенная к
на рисунке 11.6. нас
интересует приведенная к ![[a,+\infty]](/sites/default/files/tex_cache/306dccecc867dcff3827ffa2edef03eb.png) цена min-вершины
(все значения, меньшие
цена min-вершины
(все значения, меньшие  , безразличны), а после просмотра
вершины
, безразличны), а после просмотра
вершины  эта приведенная цена уже известна
(равна
эта приведенная цена уже известна
(равна  ).
Аналогичным образом цена игры с двумя исходами
).
Аналогичным образом цена игры с двумя исходами  равна ее приведенной к отрезку
равна ее приведенной к отрезку ![[-1,+1]](/sites/default/files/tex_cache/335c2d7c2ccfc1766a245197da8da7c8.png) цене, и после
обнаружения выигрышного хода становится ясным, что эта цена
равна
цене, и после
обнаружения выигрышного хода становится ясным, что эта цена
равна 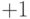 .
.Используя это соображение, напишем оптимизированный
алгоритм, в котором рекурсивно определяется приведенная
к промежутку ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) цена игры в текущей вершине:
цена игры в текущей вершине:
procedure find_reduced_cost (a,b: integer; var c: integer)
| var x: integer;
begin
| if тип = final then begin
| | c:= стоимость, приведенная к [a,b]
| end else if тип = max then begin
| | вверх_налево;
| | find_reduced_cost (a,b,c);
| | {c = максимум цены вершины и братьев слева,
| | приведенный к [a,b]
| | while есть_справа and (c<b) do begin
| | | вправо;
| | | find_reduced_cost (c,b,x);
| | | c := x;
| | end;
| | {c=цена вершины под текущей, приведенная к [a,b]}
| | вниз;
| end else begin {тип = мин}
| | ...симметрично
| end;
end;Естественный вопрос: насколько такого рода оптимизация
помогает уменьшить перебор? Мы рассмотрим простейший
пример. Пусть игра имеет фиксированную длину, из каждой
позиции возможны два хода, игроки ходят по очереди, каждый
делает  ходов и цены листьев равны
ходов и цены листьев равны  или
или  . Дерево
такой игры - полное двоичное дерево, min- и max-уровни
чередуются, в листьях написаны нули и единицы, и нужно
вычислить значение в корне. (Если считать, что
. Дерево
такой игры - полное двоичное дерево, min- и max-уровни
чередуются, в листьях написаны нули и единицы, и нужно
вычислить значение в корне. (Если считать, что  ,
,  , то максимум и минимум
соответствуют операциям OR (ИЛИ) и AND (И), поэтому иногда
говорят об AND-OR-дереве.)
, то максимум и минимум
соответствуют операциям OR (ИЛИ) и AND (И), поэтому иногда
говорят об AND-OR-дереве.)
Сколько листьев нужно посетить, чтобы вычислить значение
в корне? Напомним, что всего листьев 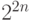 для дерева
с
для дерева
с  уровнями (каждый из игроков делает
уровнями (каждый из игроков делает  ходов).
ходов).
11.4.1.
Доказать, что для любых значений в листьях описанный нами
оптимизированный алгоритм просматривает не
менее 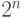 листьев.
листьев.
Решение. На уровне  находятся четыре вершины. В ходе
работы алгоритм должен узнать цену игры хотя бы в двух из
них. В самом деле, пусть нижняя вершина есть min-вершина.
Если в ней нуль, то в одном из ее сыновей тоже нуль. А раз
это max-вершина, то для установления этого факта нужно
знать цену обоих сыновей (равную нулю). Второй случай:
в корне единица. Тогда в обеих его сыновьях должна быть
единица, и чтобы быть в этом уверенным, нужно в каждом из
них посмотреть как минимум одного сына.
находятся четыре вершины. В ходе
работы алгоритм должен узнать цену игры хотя бы в двух из
них. В самом деле, пусть нижняя вершина есть min-вершина.
Если в ней нуль, то в одном из ее сыновей тоже нуль. А раз
это max-вершина, то для установления этого факта нужно
знать цену обоих сыновей (равную нулю). Второй случай:
в корне единица. Тогда в обеих его сыновьях должна быть
единица, и чтобы быть в этом уверенным, нужно в каждом из
них посмотреть как минимум одного сына.
Аналогично ради каждого значения на уровне  нужны два
значения на уровне
нужны два
значения на уровне 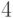 и так далее - в конце концов на
уровне
и так далее - в конце концов на
уровне  нужно знать
нужно знать 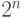 значений.
значений.
Для наглядности мы говорили о конкретном алгоритме,
описанном выше. Но справедлив и более общий факт: любой
набор значений в листьях, который однозначно определяет
значение в корне, содержит не менее 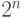 значений.
значений.
11.4.2. Провести аккуратное доказательство этого утверждения.
Указание. По существу уже все доказано, надо только это оформить.
Только что полученная оценка относилась к самому благоприятному случаю. Утверждение следующей задачи, напротив, говорит о наихудшем случае.
11.4.3. Пусть у нас спрашивают значения в листьях AND-OR-дерева в заранее неизвестном нам порядке, и мы можем называть эти значения по собственному усмотрению. Доказать, что мы можем действовать так, чтобы до последнего момента (пока есть хоть одно не названное значение) цена корня оставалось бы неизвестной (то есть могла быть и нулем, и единицей в зависимости от еще не названных значений).
Эта задача показывает, что любой алгоритм отыскания цены корня в наиболее неблагоприятном случае вынужден обходить все листья (в частности, наш оптимизированный алгоритм никакого выигрыша не дает).
Решение. Будем доказывать это индукцией по высоте дерева. Пусть корень является AND-вершиной. Тогда будем оттягивать (по предположению индукции) определение значений в детях корня, а когда дальше оттягивать будет нельзя (последний лист поддерева становится известным), сделаем так, чтобы это поддерево было истинным. Тем самым значение в корне совпадает со значением в другом поддереве и может оставаться неопределенным до последнего момента.
Более интересной является оценка среднего числа опрошенных листьев. Будем считать, что алгоритм find_reduced_cost применяется к некоторому фиксированному AND-OR-дереву (с фиксированными значениями в листьях), но для каждой вершины порядок просмотра двух ее детей выбирается случайно. Тогда общее число просмотренных листьев становится случайной величиной.
11.4.4.
Доказать, что математическое ожидание этой случайной
величины (среднее по всем порядкам просмотров) для любого
AND-OR-дерева высоты  (с
(с 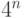 вершинами) не
превосходит
вершинами) не
превосходит  .
.
Решение. Рассмотрим сначала случай 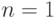 , то есть дерево
глубины
, то есть дерево
глубины  . Пусть его корень является AND-вершиной. Если
в корне находится
. Пусть его корень является AND-вершиной. Если
в корне находится  , то на первом уровне
, то на первом уровне 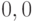 или
или 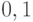 . В первом случае нам достаточно просмотреть две
вершины (найдя первый нуль, мы не ищем второй). Во втором
случае с вероятностью
. В первом случае нам достаточно просмотреть две
вершины (найдя первый нуль, мы не ищем второй). Во втором
случае с вероятностью 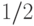 нам хватит двух, а с
вероятностью
нам хватит двух, а с
вероятностью 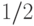 понадобится три или четыре. Если же
в AND-корне находится
понадобится три или четыре. Если же
в AND-корне находится  , то в обеих OR-вершинах первого
уровня находится единица, и на каждую из них нужно
в среднем не больше
, то в обеих OR-вершинах первого
уровня находится единица, и на каждую из них нужно
в среднем не больше  просмотров листьев
(с вероятностью не менее
просмотров листьев
(с вероятностью не менее 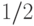 мы сразу попадаем в лист
с единицей и второй лист не смотрим).
мы сразу попадаем в лист
с единицей и второй лист не смотрим).
Дальнейшее рассуждение легко происходит по индукции. Пусть
среднее значение числа запрашиваемых листьев для любого
дерева глубины 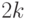 не превосходит
не превосходит 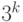 . Рассмотрим
дерево
глубины
. Рассмотрим
дерево
глубины  с фиксированными значениями в листьях. Для
каждого выбора порядка на первых двух уровнях известно,
какие из четырех вершин высоты
с фиксированными значениями в листьях. Для
каждого выбора порядка на первых двух уровнях известно,
какие из четырех вершин высоты  будут рассмотрены. По
предположению среднее число использованных листьев при
рассмотрении каждой вершины высоты
будут рассмотрены. По
предположению среднее число использованных листьев при
рассмотрении каждой вершины высоты  (усреднение по всем
порядкам обхода) не больше
(усреднение по всем
порядкам обхода) не больше 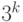 . Дополнительно усредняем
по порядкам на двух первых уровнях и замечаем, что
в среднем рассматривается не больше трех вершин высоты
. Дополнительно усредняем
по порядкам на двух первых уровнях и замечаем, что
в среднем рассматривается не больше трех вершин высоты  .
.
11.4.5.
Получить более точную оценку для числа просмотренных
листьев в предыдущей задаче. Используйте разные
оценки в зависимости от значения в корне; это позволит
заменить 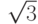 в оценке на меньшее число
в оценке на меньшее число  .]
.]