| Россия, Пошатово |
Анализ игр
11.2.4. Игра в крестики-нолики состоит в следующем: на большом квадратном поле два игрока по очереди ставят крестики и нолики в еще не занятые клетки (начинают крестики). Выигрывает тот, кто первым поставит пять своих знаков подряд (по вертикали, горизонтали или диагонали). Если все поле заполнено, а такого не случилось, партия считается ничейной. Доказать, что у крестиков есть стратегия, гарантирующая им ничью или выигрыш.
Решение. Согласно теореме Цермело, в противном случае у ноликов есть стратегия, гарантирующая им выигрыш. Покажем, что крестики могут использовать по существу ту же стратегию, забыв о своем первом ходе. А именно, представим себе, что крестики делают произвольный первый ход (карандашом), а затем отвечают (чернилами) на ходы ноликов по выигрышной стратегии для ноликов (считая ходы ноликов крестиками и забыв о своем первом ходе).
Может ли при этом первый ход помешать? Может, если стратегия указывает как раз на ту клетку, где уже стоит карандашный крестик. В этом случае надо карандашный крестик обвести чернилами, а карандашом сделать ход в любую свободную клетку. Если свободных клеток нет, то позиция соответствует (с точностью до замены крестиков на нолики) заключительной позиции в выигрышной партии для ноликов, и потому является выигрышной.
Кроме того, игра может кончиться раньше времени, если карандашный крестик образует выигрышный ряд с чернильными - но это нам только лучше.
Таким образом, мы доказали, что если у ноликов есть выигрышная стратегия, то и у крестиков есть выигрышная стратегия - и если дать этим стратегиям играть друг против друга, получится противоречие.
11.2.5. Доказать, что цена любой игры равна выигрышу в одной из заключительных вершин.
11.2.6. Показать, что теорема Цермело вытекает из своего частного случая игр с двумя исходами (выигрыш первого и второго).
Указание.
Для каждого  будем считать выигрыш меньше
будем считать выигрыш меньше  проигрышем, а больше
проигрышем, а больше  - выигрышем.
- выигрышем.
11.2.7.
Пусть дана некоторая игра  . Выберем одну из
заключительных вершин и будем менять выигрыш в этой
вершине: положив его равным
. Выберем одну из
заключительных вершин и будем менять выигрыш в этой
вершине: положив его равным  , получим игру
, получим игру ![G[c]](/sites/default/files/tex_cache/46735a8367c44e98352efe18e7ed551b.png) .
Рассмотрим цену этой игры как функцию от
.
Рассмотрим цену этой игры как функцию от  . Что это может
быть за функция?
. Что это может
быть за функция?
Ответ. цена игры ![G[c]](/sites/default/files/tex_cache/46735a8367c44e98352efe18e7ed551b.png) равна ближайшей к
равна ближайшей к  точке
некоторого отрезка
точке
некоторого отрезка ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) (зависящего от игры
(зависящего от игры  ).
).
Вот еще один пример игры, где теорема Цермело позволяет
доказать существование выигрышной стратегии для первого
игрока. Эта игра названа в книгах М. Гарднера
("Математические досуги", М.: Мир, 1972; "
Математические головоломки и развлечения", М.: Мир, 1971)
игрой Гейла или "бридж-ит".
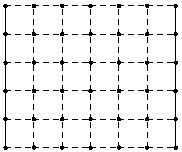
Рассмотрим прямоугольную сеть из пунктирных линий
высоты  и ширины
и ширины  (
рис. 11.2.);
(
рис. 11.2.);
 .
Первый игрок каждым своим ходом обводит (сплошной линией)
один из отрезков. Его задача - соединить сплошными линиями
левую и правую стороны прямоугольника. Задача второго
игрока - ему помешать; каждым своим ходом он стирает один
из отрезков (лишая первого возможности впоследствии его
обвести). Игра заканчивается, когда все отрезки обведены
или стерты; первый выиграл, если при этом левая и правая
стороны прямоугольника соединены.
.
Первый игрок каждым своим ходом обводит (сплошной линией)
один из отрезков. Его задача - соединить сплошными линиями
левую и правую стороны прямоугольника. Задача второго
игрока - ему помешать; каждым своим ходом он стирает один
из отрезков (лишая первого возможности впоследствии его
обвести). Игра заканчивается, когда все отрезки обведены
или стерты; первый выиграл, если при этом левая и правая
стороны прямоугольника соединены.11.2.8. Используя теорему Цермело, доказать, что первый игрок имеет выигрышную стратегию.
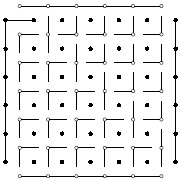
Указание. Игру можно представить в более симметричном виде, если добавить сетку для второго игрока (рис. 11.3.) и считать, что второй хочет соединить верхнюю и нижнюю стороны своей сетки, а линиям первого и второго игроков запрещено пересекаться (тем самым проведя свою линию, второй игрок как бы стирает пересекающую ее линию первого). Если игра закончилась (в каждой возможной точке пересечения проведена вертикальная или горизонтальная линия), то ровно один из игроков выиграл: можно пройти по линиям или слева направо, или сверху вниз, но не одновременно. Аккуратное доказательство этого интуитивно ясного топологического факта, впрочем, не так просто.
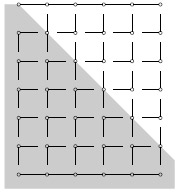
Как пишет Гарднер, Клод Шеннон (создатель теории информации) придумал для этой игры любопытную "физическую" стратегию, которая легко обобщается на любую сеть линий. Представим себе, что все стороны всех клеток сети (для первого игрока) представляют собой резисторы одинакового сопротивления, кроме левой и правой сторон прямоугольника, которые сделаны из провода нулевого сопротивления. Первый игрок своим ходом закорачивает эти сопротивления, а второй игрок разрывает их (делает бесконечными). Стратегия первого игрока состоит в том, что надо подключить напряжение между левой и правой сторонами прямоугольника, и закорачивать (обводить) то сопротивление, через которое идет максимальный ток (или, что то же самое, на котором падает наибольшая разность потенциалов). Если таких сопротивлений оказалось несколько, можно закорачивать любое из них.Из книг Гарднера не ясно, является ли эта стратегия выигрышной. Зато там приведена явная выигрышная стратегия (со ссылкой на О. Гросса). Чтобы объяснить ее, будем считать, что целью первого игрока является не дать второму соединить верх и низ. (Мы уже упоминали, что эта цель равносильна исходной.) Начальный ход первого игрока показан на рис. 11.4.; этот ход запрещает одно из ребер второго игрока. Разделим остальные ребра второго игрока на пары соседних, как показано на том же рисунке. Первый игрок препятствует второму провести оба ребра какой-либо пары: если второй провел одно из ребер пары, первый не дает провести второе ребро этой пары (проведя пересекающее его свое ребро).
Следующая задача показывает, что эта стратегия является выигрышной (первый игрок не дает второму соединить верх и низ и потому соединяет левую и правую стороны).11.2.9. Доказать, что любой путь по линиям пунктирной сетки, соединяющий верх и низ рисунка 11.4., обязательно покрывает два ребра одной пары.
Решение. Для ясности оставим на рисунке только пунктирные линии и соответствующие вершины (рис. 11.5.). Отметим серую область, как показано на рисунке; тем самым ребра делятся на серые и белые. Предположим, что имеется путь снизу вверх, который не покрывает ни одной пары ребер. Можно считать, что этот путь
не проходит дважды через одну вершину (выбросим циклы). Каждый шаг на этом пути может относиться к одной из восьми категорий: четыре направления (север, восток, юг и запад) комбинируются с двумя цветами (серым и белым). Как видно из рисунка, путь должен начинаться с серого шага на север, а заканчиваться белым шагом на север.Покажем, что это невозможно в силу наших ограничений (нельзя использовать два ребра одной пары и нельзя дважды проходить через одну вершину). Что, к примеру, может следовать за серым шагом на север? Еще один серый шаг на север, серый шаг на запад или белый шаг на восток. За серым шагом на запад может следовать серый шаг на запад или серый шаг на север. Разбирая поочередно все варианты, легко убедиться, что путь, начавшись серым шагом на север, никогда не выйдет (если не нарушит правил) за пределы множества

11.2.10. Двое играют на бесконечной клетчатой бумаге, по очереди обводя красным и синим стороны клеток (за один ход можно обвести одну сторону любой клетки, если она еще не обведена). Доказать, что второй может воспрепятствовать первому построить замкнутый путь из линий своего цвета.
Указание. Он может помешать первому, например, повернуть с запада на север, разбив все стороны клеток на пары и не давая покрыть оба члена пары.
11.2.11.
(Для знакомых с теорией вероятностей) На поле для игры
Гейла (рис. 11.2.) каждая из пунктирных
линий
обведена с вероятностью 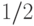 независимо от других.
Доказать, что путь от левой до правой стороны (по
обведенным линиям) существует с вероятностью
независимо от других.
Доказать, что путь от левой до правой стороны (по
обведенным линиям) существует с вероятностью 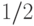 .
.