Сопоставление с образцом

Надо понять, как поддерживать это при добавлении очередного суффикса. Можно, не мудрствуя лукаво, добавлять 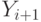буква за буквой, начиная с корня дерева. (Именно так мы раньше и делали, и это требовало квадратичного времени.)

Какие тут возможны оптимизации? Первая связана с тем, что мы можем двигаться по дереву быстрее, если знаем, что заведомо из него не выйдем. Вторая связана с использованием суффиксных ссылок.

Оба варианта предполагают, что отец листа не совпадает с корнем. (Если совпадает, нам придется добавлять 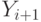от корня.) Пусть 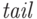- пометка листа , а 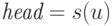; другими словами, слово соответствует вершине . Тогда

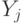Заметим, что заведомо не выходит за пределы дерева. В самом деле, было точкой ветвления, поэтому помимо листа через точку проходил и лист с . Тогда 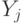начинается на , а 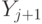начинается на и уже есть в дереве.

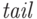Поэтому мы можем сначала проследить (найти позицию , для которой ), а потом уже добавить , начиная с .

Первый способ оптимизации: заведомо есть в дереве.

Эта оптимизация никак не использует суффиксных ссылок. Второй способ оптимизации их использует и позволяет (в том случае, когда применим) обойтись без прослеживания 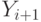от корня (как ускоренного, так и обычного). Пусть на пути к листу , представляющему суффикс , имеется вершина , у которой суффиксная ссылка указывает на вершину , так что . Пусть - слово на пути от к .

Тогда

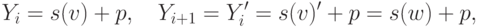
и для добавления 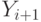в дерево достаточно добавить слово , начиная с вершины .

Второй способ оптимизации сочетается с первым: отрезок слова от до отца листа можно проходить с уверенностью, что мы не выйдем за пределы дерева.

Итак, мы можем описать действия, выполняемые при добавление очередного суффикса 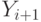в дерево, следующим образом.

Второй способ оптимизации: пользуемся суффиксной ссылкой вершины на пути к .

Пусть - отец листа , соответствующего последнему уже добавленному суффиксу .

Случай 1: есть корень дерева. Тогда ни одна из оптимизаций не применима, и мы добавляем 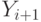, начиная от корня.

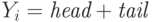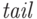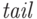Случай 2: не есть корень дерева, но отец есть корень дерева (лист находится на высоте ). Тогда , где и - пометки вершин и . Мы применяем первую оптимизацию и прослеживаем с гарантией до некоторой позиции , а потом добавляем от .

Случай 3: не есть корень дерева и его отец также не есть корень дерева. Тогда для имеется суффиксная ссылка на некоторую вершину , и . Пусть - пометка вершины , а 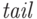- пометка листа , при этом и потому 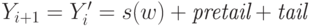. Остается проследить от вершины с гарантией, получив некоторую позицию , а потом добавить 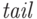от вершины .

Остается еще понять, как поддерживать структуру суффиксных ссылок (адрес нового листа у нас получается при добавлении сам собой, так что с ним проблем нет) и оценить число действий при выполнении этих процедур последовательно для всех суффиксов.

Начнем с суффиксных ссылок. По правилам они должны быть у всех внутренних вершин, кроме отца только что добавленного листа. Поэтому нам надо заботиться об отце листа , соответствующего (этот лист перестал быть "только что добавленным"; напротив, единственная новая вершина как раз является отцом только что добавленного листа и в ней суффиксная ссылка не нужна). Это актуально в случаях 2 и 3, но в этих случаях по ходу дела была найдена нужная вершина , куда и будет направлена суффиксная ссылка из . Строго говоря, могла быть не вершиной, а позицией, но тогда после добавления она станет вершиной (отцом только что добавленного листа) - ведь в новом дереве уже не является отцом последнего листа, и потому суффиксная ссылка из , как было доказано, должна вести в вершину. (Другими словами, в случаях 2 и 3, если позиция была внутри ребра, то в ней ребро разрезается.)

Все сказанное можно условно записать в виде такого алгоритма добавления суффикса :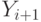

{ дерево содержит суффиксы Y1,...,Yi
  s(last)=Yi
  имеются корректные суффиксные ссылки для всех
  внутренних вершин, кроме отца листа last} 
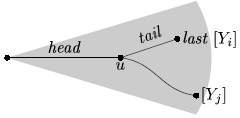
u :=  отец листа last;
tail := пометка листа last;
Yi=s(u)+tail 
if u=корень дерева then begin
| {Yi+1=tail'}  
| добавить tail', начиная с корня,
|    полученный лист поместить в last
end else begin}
| v := отец вершины u;
| pretail := пометка вершины u;
| {Yi=s(v)+pretail}+tail}
| if v = корень дерева then begin
| | {Yi+1=pretail'+tail} 
| | проследить pretail' из корня в z
| end else begin
| | w := суффиксная ссылка вершины v;
| | s(w)=s(v)', Yi+1=s(w)+pretail+tail} 
| | проследить pretail из w в z
| end;
| {осталось добавить tail из z и ссылку из u в z}
| if позиция z является вершиной then begin
| | поместить в u ссылку на z;
| | добавить tail, начиная с z,
| |     полученный лист поместить в last;
| end else begin
| добавить tail, начиная с z,
|     полученный лист поместить в last;
| поместить в u ссылку на отца листа last;
| end
end;

Осталось оценить число действий, которые выполняются при последовательном добавлении суффиксов . При добавлении каждого следующего суффикса выполняется конечное число действий, если не считать действий при "прослеживании" и "добавлении". Нам надо установить, что общее число действий есть ; для этого достаточно отдельно доказать, что суммарное число действий при всех прослеживаниях есть и суммарное число действий при всех добавлениях есть . (Заметим, что некоторые прослеживания или добавления могут быть долгими - но это компенсируется другими.)

Прослеживания. Длительность прослеживания пропорциональна числу задействованных в нем ребер, но при этом высота последнего добавленного листа (число ребер на пути к нему) увеличивается на 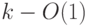(по сравнению с предыдущим добавленным листом). Чтобы убедиться в этом, достаточно заметить, что в третьем случае высота вершины 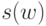может быть меньше высоты вершины 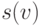разве что на единицу, поскольку суффиксные ссылки из всех вершин на пути к (не считая корня, где нет суффиксной ссылки) ведут в вершины на пути к . Поскольку высота любого листа ограничена числом , заключаем, что общая длительность всех прослеживаний есть .

Добавления. Рассуждаем аналогично, но следим не за высотой последнего листа, а за длиной его пометки. При добавлении слова 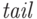(или ) число действий пропорционально числу просмотренных букв, но каждая просмотренная буква (кроме, быть может, одной) уменьшает длину пометки хотя бы на единицу: в пометке остаются лишь непросмотренные буквы (не считая первой). Поэтому на все добавления уходит в общей сложности действий.

Тем самым мы доказали, что описанный алгоритм строит сжатое суффиксное дерево слова длины за действий. После этого для любого слова длины можно за действий выяснить, является ли подсловом слова .

10.8.8. Как модифицировать алгоритм построения суффиксного дерева, чтобы не только узнавать, является ли данное слово подсловом слова , но и (если является) указывать место, где оно встречается (одно из таких мест, если их несколько)? Время построения должно оставаться 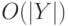, время поиска подслова - .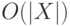

Решение. Каждая вершина сжатого суффиксного дерева соответствует некоторому подслову слова ; в момент, когда эта вершина была добавлена в дерево, известно, в каком месте есть такое подслово, и можно записать в вершине, где соответствующее подслово кончается.

10.8.9. Как модифицировать этот алгоритм, чтобы для каждого подслова можно было бы указывать его первое (самое левое) вхождение?

Указание. При возникновении новой вершины на ребре нужно брать ее первое вхождение (информация о котором есть на конце ребра), а не второе, только что обнаруженное.

10.8.10. Как модифицировать этот алгоритм, чтобы для каждого подслова можно было бы указывать его последнее (самое правое) вхождение?

Указание. Если при каждом проходе корректировать информацию вдоль пути, это будет долго; быстрее построить дерево, затем вновь его обойти и для каждой вершины вычислить момент последнего появления соответствующего подслова.

10.8.11. Как использовать сжатое суффиксное дерево, чтобы для данного слова за время 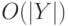найти самое длинное подслово, которое входит в более одного раза?

Решение. Такое подслово является внутренней вершиной суффиксного дерева, поэтому достаточно из всех его вершин взять ту, которой соответствует самое длинное слово. Для этого достаточно обойти все его вершины (длину можно вычислять по мере обхода, складывая длины пометок на ребрах).

На практике можно использовать также и другой способ нахождения самого длинного подслова, входящего дважды, - так называемый массив суффиксов. А именно, будем рассматривать число как "код" конца слова, начинающего с -ой буквы. Введем на кодах порядок, соответствующий лексикографическому (словарному) порядку на словах: код предшествует коду , если конец слова, начинающийся с , в лексикографическом порядке идет раньше конца слова, начинающегося с . После этого отсортируем коды в соответствии с этим порядком, получив некоторую перестановку массива 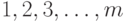(где - длина исходного слова ). Если какое-то слово входит в слово дважды, то оно является началом двух концов слова . При этом эти концы можно выбрать соседними в лексикографическом порядке, поскольку все промежуточные слова тоже начинаются на . Значит, достаточно для всех соседних концов посмотреть, сколько начальных букв у них совпадает, и взять максимум.

Этот способ требует меньше памяти (нам нужен лишь один массив из целых чисел той же длины, что исходное слово), но может требовать большого времени: во-первых, сортировка сама по себе требует порядка 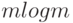сравнений, во-вторых, каждое сравнение может длиться долго, если совпадающий кусок большой. Но в случаях, когда длинных совпадающих кусков мало, такой алгоритм работает неплохо.

10.8.12. Применить один из таких алгоритмов к любимой книге и объяснить результат.

Указание. Длинные повторяющиеся куски могут быть художественным приемом (как в известном стишке про дом, который построил Джек) или следствием забывчивости автора. Для современных авторов возможно также неумеренное использование функций вырезания и вставки (заливки текста в мышь и выливания из мыши, если использовать графический интерфейс) в текстовом редакторе.