| Россия, Пошатово |
Сопоставление с образцом
10.3. Вспомогательные утверждения
Для произвольного слова  рассмотрим все его начала,
одновременно являющиеся его концами, и выберем из них самое
длинное. (Не считая, конечно, самого слова
рассмотрим все его начала,
одновременно являющиеся его концами, и выберем из них самое
длинное. (Не считая, конечно, самого слова  .) Будем
обозначать его
.) Будем
обозначать его 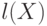 .
.
Примеры: 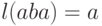 ,
, 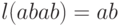 ,
, 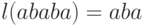 ,
, 
10.3.1.
Доказать, что все слова 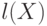 ,
,  ,
, 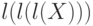 и т.д. являются началами слова
и т.д. являются началами слова  .
.
Решение. Каждое из них (согласно определению) является началом предыдущего.
По той же причине все они являются концами слова  .
.
10.3.2. Доказать, что последовательность предыдущей задачи обрывается (на пустом слове).
Решение. Каждое слово короче предыдущего.
10.3.3.
Доказать, что любое слово, одновременно являющееся началом
и концом слова  (кроме самого
(кроме самого  ) входит
в последовательность
) входит
в последовательность 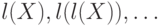
Решение. Пусть слово  есть одновременно начало
и конец
есть одновременно начало
и конец  . Слово
. Слово 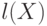 - самое длинное из таких слов,
так что
- самое длинное из таких слов,
так что  не длиннее
не длиннее 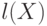 . Оба эти слова являются
началами
. Оба эти слова являются
началами  , поэтому более короткое из них является
началом более длинного:
, поэтому более короткое из них является
началом более длинного:  есть начало
есть начало 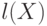 .
Аналогично,
.
Аналогично,  есть конец
есть конец 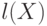 . Рассуждая по индукции, можно
предполагать, что утверждение задачи верно для всех слов
короче
. Рассуждая по индукции, можно
предполагать, что утверждение задачи верно для всех слов
короче  , в частности, для слова
, в частности, для слова 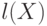 . Так что
слово
. Так что
слово  , являющееся концом и началом
, являющееся концом и началом 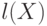 , либо равно
, либо равно 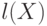 , либо входит в последовательность
, либо входит в последовательность 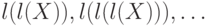 , что и требовалось доказать.
, что и требовалось доказать.
10.4. Алгоритм Кнута-Морриса-Пратта
Алгоритм Кнута-Морриса-Пратта (КМП) получает на вход слово
![{X}= {x[1]x[2]}\ldots{x[n]}](/sites/default/files/tex_cache/6e551b8ab9a74a63434ef81bb976c2cf.png)
![{l[1]}\ldots{l[n]}](/sites/default/files/tex_cache/e18a0acff66336ae2426f59a643da7b2.png) ,
где
,
где![{l[i]} = \text{длина слова }l({x[1]}\ldots{x[i]})](/sites/default/files/tex_cache/a314701c45eb32d321e7d9bfa97877f4.png)
 определена в предыдущем пункте). Словами: l[i] есть длина наибольшего начала слова
определена в предыдущем пункте). Словами: l[i] есть длина наибольшего начала слова ![{x[1]}\ldots{x[i]}](/sites/default/files/tex_cache/19c196009c13db29b369db0a4b0a7758.png) , одновременно являющегося его
концом.
, одновременно являющегося его
концом.10.4.1. Какое отношение все это имеет к поиску подслова? Другими словами, как использовать алгоритм КМП для определения того, является ли слово A подсловом слова B?
Решение. Применим алгоритм КМП к слову A\#B, где \# - специальная буква, не встречающаяся ни в A, ни в B. Слово A является подсловом слова B тогда и только тогда, когда среди чисел в массиве l будет число, равное длине слова A.
10.4.2.
Описать алгоритм заполнения таблицы ![{l[1]}\ldots{l[n]}](/sites/default/files/tex_cache/e18a0acff66336ae2426f59a643da7b2.png) .
.
Решение. Предположим, что первые i значений ![{l[1]}\ldots{l[i]}](/sites/default/files/tex_cache/0a5413b31e62ba43bf71b5025a6bb889.png) уже найдены. Мы читаем очередную
букву слова (т.е. x[i+1] ) и должны вычислить l[i+1].
уже найдены. Мы читаем очередную
букву слова (т.е. x[i+1] ) и должны вычислить l[i+1].
Другими словами, нас интересуют начала  слова
слова ![{x[1]}\ldots{x[i+1]}](/sites/default/files/tex_cache/6f024cfa21c058afabefbaf26e5a4bee.png) , одновременно являющиеся его
концами - из них нам надо выбрать самое длинное. Откуда
берутся эти начала? Каждое из них (не считая пустого)
получается из некоторого слова
, одновременно являющиеся его
концами - из них нам надо выбрать самое длинное. Откуда
берутся эти начала? Каждое из них (не считая пустого)
получается из некоторого слова 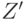 приписыванием буквы x[i+1]. Слово
приписыванием буквы x[i+1]. Слово 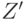 является началом и концом слова
является началом и концом слова ![{x[1]}\ldots{x[i]}](/sites/default/files/tex_cache/19c196009c13db29b369db0a4b0a7758.png) . Однако не любое слово, являющееся
началом и концом слова
. Однако не любое слово, являющееся
началом и концом слова ![{x[1]}\ldots{x[i]}](/sites/default/files/tex_cache/19c196009c13db29b369db0a4b0a7758.png) , годится -
надо, чтобы за ним следовала буква x[i+1].
, годится -
надо, чтобы за ним следовала буква x[i+1].
Получаем такой рецепт отыскания слова  . Рассмотрим все
начала слова
. Рассмотрим все
начала слова ![{x[1]}\ldots{x[i]}](/sites/default/files/tex_cache/19c196009c13db29b369db0a4b0a7758.png) , являющиеся
одновременно его концами. Из них выберем подходящие - те,
за которыми идет буква
, являющиеся
одновременно его концами. Из них выберем подходящие - те,
за которыми идет буква ![{x[i+1]}](/sites/default/files/tex_cache/b2080e704223f253395f32270815b356.png) . Из подходящих выберем
самое длинное. Приписав в его конец x[i+1], получим
искомое слово
. Из подходящих выберем
самое длинное. Приписав в его конец x[i+1], получим
искомое слово  .
.
Теперь пора воспользоваться сделанными нами приготовлениями
и вспомнить, что все слова, являющиеся одновременно
началами и концами данного слова, можно получить повторными
применениями к нему функции  из предыдущего раздела. Вот
что получается:
из предыдущего раздела. Вот
что получается:
i:=1; l[1]:= 0;
{таблица l[1]..l[i] заполнена правильно}
while i <> n do begin
| len := l[i]
| {len - длина начала слова x[1]..x[i], которое является
| его концом; все более длинные начала оказались
| неподходящими}
| while (x[len+1] <> x[i+1]) and (len > 0) do begin
| | {начало не подходит, применяем к нему функцию l}
| | len := l[len];
| end;
| {нашли подходящее или убедились в отсутствии}
| if x[len+1] = x[i+1] do begin
| | {x[1]..x[len] - самое длинное подходящее начало}
| | l[i+1] := len+1;
| end else begin
| | {подходящих нет}
| | l[i+1] := 0;
| end;
| i := i+1;
end;10.4.3.
Доказать, что число действий в приведенном только что
алгоритме не превосходит 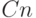 для некоторой
константы
для некоторой
константы  .
.
Решение. Это не вполне очевидно: обработка каждой очередной буквы может потребовать многих итераций во внутреннем цикле. Однако каждая такая итерация уменьшает len по крайней мере на 1, и в этом случае l[i+1] окажется заметно меньше l[i]. С другой стороны, при увеличении i на единицу величина l[i] может возрасти не более чем на 1, так что часто и сильно убывать она не может - иначе убывание не будет скомпенсировано возрастанием.
Более точно, можно записать неравенство
![{l[i+1]} \le {l[i]} - \hbox{(число итераций на {i}-м шаге)} + {1}](/sites/default/files/tex_cache/b58734ce601a95f1a6a60c3991394c82.png)
![\hbox{(число итераций на {i}-м шаге)}\le{l[i]}-{l[i+1]} + {1}.](/sites/default/files/tex_cache/5f884855b67296c54a707713d8a39c27.png)
10.4.4.
Будем использовать этот алгоритм, чтобы выяснить, является
ли слово X длины n подсловом слова Y
длины m. (Как это делать с помощью специального
разделителя \#, описано выше.) При этом число действий
будет не более 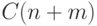 , и используемая память
тоже. Придумать, как обойтись памятью не более
, и используемая память
тоже. Придумать, как обойтись памятью не более 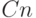 (что может быть существенно меньше, если искомый образец
короткий, а слово, в котором его ищут - длинное).
(что может быть существенно меньше, если искомый образец
короткий, а слово, в котором его ищут - длинное).
Решение. Применяем алгоритм КМП к слову 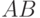 . При
этом вычисление значений
. При
этом вычисление значений ![{l[1]},\ldots,{l[n]}](/sites/default/files/tex_cache/cb3333a865fc581cd96eb9271d546322.png) проводим для слова X длины n и запоминаем эти
значения. Дальше мы помним только значение l[i] для
текущего i - кроме него и кроме таблицы
проводим для слова X длины n и запоминаем эти
значения. Дальше мы помним только значение l[i] для
текущего i - кроме него и кроме таблицы ![{l[1]}\ldots{l[n]}](/sites/default/files/tex_cache/e18a0acff66336ae2426f59a643da7b2.png) , нам для вычислений ничего не
нужно.
, нам для вычислений ничего не
нужно.
На практике слова X и Y могут не находиться подряд, поэтому просмотр слова X и затем слова Y удобно оформить в виде разных циклов. Это избавляет также от хлопот с разделителем.
10.4.5.
Написать соответствующий алгоритм (проверяющий, является ли
слово ![{X}={x[1]}\ldots{x[n]}](/sites/default/files/tex_cache/293f2c9736e44dceacc9a4a099e8221a.png) подсловом слова
подсловом слова ![{Y}={y[1]}\ldots{y[m]}](/sites/default/files/tex_cache/44b70d6e9a38d4134c74c23df4122597.png) ).
).
Решение. Сначала вычисляем таблицу ![{l[1]}\ldots{l[n]}](/sites/default/files/tex_cache/e18a0acff66336ae2426f59a643da7b2.png) как раньше. Затем пишем такую
программу:
как раньше. Затем пишем такую
программу:
j:=0; len:=0;
{len - длина максимального начала слова X, одновременно
являющегося концом слова y[1]..y[j]}
while (len <> n) and (j <> m) do begin
| while (x[len+1] <> y[j+1]) and (len > 0) do begin
| | {начало не подходит, применяем к нему функцию l}
| | len := l[len];
| end;
| {нашли подходящее или убедились в отсутствии}
| if x[len+1] = y[j+1] do begin
| | {x[1]..x[len] - самое длинное подходящее начало}
| | len := len+1;
| end else begin
| | {подходящих нет}
| | len := 0;
| end;
| j := j+1;
end;
{если len=n, слово X встретилось; иначе мы дошли до конца
слова Y, так и не встретив X}
