Рекурсия

7.4.4. Где использован тот факт, что граф не имеет циклов?

Решение. Мы опустили доказательство конечности глубины рекурсии. Для каждой вершины рассмотрим ее "глубину" - максимальную длину пути по стрелкам, из нее выходящего. Условие отсутствия циклов гарантирует, что эта величина конечна. Из вершины нулевой глубины стрелок не выходит. Глубина конца стрелки по крайней мере на меньше, чем глубина начала. При работе процедуры все рекурсивные вызовы 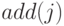относятся к вершинам меньшей глубины.

Вернемся к оценке времени работы. Сколько вызовов возможно для какого-то фиксированного 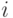? Прежде всего ясно, что первый из них печатает 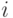, остальные сведутся к проверке того, что 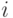уже напечатано. Ясно также, что вызовы индуцируются "печатающими" (первыми) вызовами 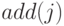для тех 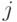, из которых в 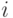ведет ребро. Следовательно, число вызовов равно числу входящих в 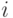ребер (стрелок). При этом все вызовы, кроме первого, требуют 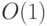операций, а первый требует времени, пропорционального числу исходящих из 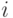стрелок. (Не считая времени, уходящего на выполнение 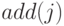для концов 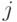выходящих ребер.) Отсюда видно, что общее время пропорционально числу ребер (плюс число вершин).

Связная компонента графа. Неориентированный граф - набор точек (вершин), некоторые из которых соединены линиями (ребрами). Неориентированный граф можно считать частным случаем ориентированного графа, в котором для каждой стрелки есть обратная.

Связной компонентой вершины 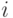называется множество всех тех вершин, в которые можно попасть из 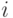, идя по ребрам графа. (Поскольку граф неориентированный, отношение " 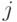принадлежит связной компоненте 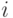" является отношением эквивалентности.)

7.4.5. Дан неориентированный граф (для каждой вершины указано число соседей и массив номеров соседей, как в задаче о топологической сортировке). Составить алгоритм, который по заданному 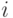печатает все вершины связной компоненты 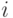по одному разу (и только их). Число действий не должно превосходить 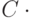(общее число вершин и ребер в связной компоненте).

Решение. Программа в процессе работы будет "закрашивать" некоторые вершины графа. Незакрашенной частью графа будем называть то, что останется, если выбросить все закрашенные вершины и ведущие в них ребра. Процедура закрашивает связную компоненту 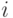в незакрашенной части графа (и не делает ничего, если вершина 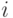уже закрашена).

procedure  add (i:1..n);
begin
| if вершина i закрашена then begin
| | ничего делать не надо
| end else begin
| | закрасить i (напечатать и пометить как закрашенную)
| | для всех j, соседних с i
| | | add(j);
| | end;
| end;
end;

Докажем, что эта процедура действует правильно (в предположении, что рекурсивные вызовы работают правильно). В самом деле, ничего, кроме связной компоненты незакрашенного графа, она закрасить не может. Проверим, что вся она будет закрашена. Пусть 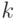- вершина, доступная из вершины 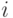по пути 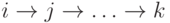, проходящему только по незакрашенным вершинам. Будем рассматривать только пути, не возвращающиеся снова в 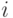. Из всех таких путей выберем путь с наименьшим 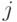(в порядке просмотра соседей в процедуре). Тогда при рассмотрении предыдущих соседей ни одна из вершин пути 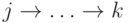не будет закрашена (иначе 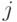не было бы минимальным) и потому 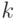окажется в связной компоненте незакрашенного графа к моменту вызова 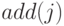. Что и требовалось.

Чтобы установить конечность глубины рекурсии, заметим, что на каждом уровне рекурсии число незакрашенных вершин уменьшается хотя бы на .

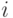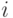Оценим число действий. Каждая вершина закрашивается не более одного раза - при первым вызове с данным . Все последующие вызовы происходят при закрашивании соседей - количество таких вызовов не больше числа соседей - и сводятся к проверке того, что вершина уже закрашена. Первый же вызов состоит в просмотре всех соседей и рекурсивных вызовах 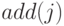для всех них. Таким образом, общее число действий, связанных с вершиной 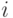, не превосходит константы, умноженной на число ее соседей. Отсюда и вытекает требуемая оценка.

7.4.6. Решить ту же задачу для ориентированного графа (напечатать все вершины, доступные из данной по стрелкам; граф может содержать циклы).

Ответ. Годится по существу та же программа (строку "для всех соседей" надо заменить на "для всех вершин, куда ведут стрелки").

Следующий вариант задачи о связной компоненте имеет скорее теоретическое значение (и называется теоремой Сэвича).

7.4.7. Ориентированный граф имеет 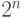вершин (двоичные слова длины ) и задан в виде функции есть_ребро, которая по двум вершинам и сообщает, есть ли в графе ребро из в . Составить алгоритм, который для данной пары вершин и определяет, есть ли путь (по ребрам) из в , используя память, ограниченную многочленом от . (Время при этом может быть - и будет - очень большим.)

Указание. Использовать рекурсивную процедуру, выясняющую, существует ли путь из в длины не более 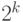(и вызывающую себя с уменьшенным на единицу значением ).

Быстрая сортировка Хоара. В заключение приведем рекурсивный алгоритм сортировки массива, который на практике является одним из самых быстрых. Пусть дан массив . Рекурсивная процедура сортирует участок массива с индексами из полуинтервала , то есть , не затрагивая остального массива.

procedure sort (l,r: integer);
begin
| if l = r then begin
| | ничего делать не надо - участок пуст
| end else begin
| | выбрать случайное число s в полуинтервале (l,r]
| | b := a[s]
| | переставить элементы сортируемого участка так, чтобы
| |   сначала шли элементы, меньшие b - участок (l,ll]
| |   затем элементы, равные b- участок (ll,rr]
| |   затем элементы, большие b       - участок (rr,r]
| | sort (l,ll);
| | sort (rr,r);
| end;
end;

Разделение элементов сортируемого участка на три категории (меньшие, равные, больше) рассматривалась в "Переменные, выражения, присваивания" (это можно сделать за время, пропорциональное длине участка). Конечность глубины рекурсии гарантируется тем, что длина сортируемого участка на каждом уровне рекурсии уменьшается хотя бы на .