| Украина |
Инспектор
Вы можете этот курс.
Опубликован: 27.12.2010 | Уровень: специалист | Доступ: платный
Лекция 2:
Графика: основные принципы
Более подробное описание основных примитивов (по алфавиту)
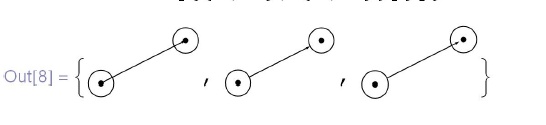
1. Задавая стрелку 
, можно кроме концов указывать отступы от них (второй аргумент), которые могут быть как одинаковыми, так и разными (окружности нарисованы для наглядности):
![\tt
In[8]:=\{Graphics[\{Arrow[\{\{0, 0\}, \{2, 1\}\}], Circle[\{0,0\}, 0.3], \\
\phantom{In[8]:=\{Gr}Circle[\{2,1\}, 0.3], Point[\{\{0,0\}, \{2,1\}\}]\}], \\
\phantom{In[8]:=\{}Graphics[\{Arrow[\{\{0,0\},\{2,1\}\}, .3], Circle[\{0,0\}, 0.3], \\
\phantom{In[8]:=\{Gr}Circle[\{2,1\}, 0.3], Point[\{\{0,0\}, \{2,1\}\}]\}], \\
\phantom{In[8]:=\{}Graphics[\{Arrow[\{\{0,0\}, \{2,1\}\}, \{.3, .1\}], \\
\phantom{In[8]:=\{Gr}Circle[\{0,0\}, 0.3], Circle[\{2,1\}, .3], \\
\phantom{In[8]:=\{Gr}Point[\{\{0,0\}, \{2,1\}\}]\}]\}](/sites/default/files/tex_cache/88ae5c05aa58b91ebb918e99061aee4b.png)
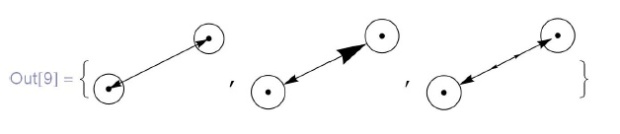
Можно также управлять размером и расположением стрелочек, используя директиву 
. Элементы списка задают направление (знак) и относительный размер стрелки (число). Абсолютный размер можно задавать командами 
:
![\tt
In[9]:= \\ \\
\phantom{In}\{Graphics[\{Arrowheads[\{-.1, .1}], Arrow[\{\{0,0\}, \{2,1\}\}], \\
\phantom{In[9]:}Circle[\{0,0\}, 0.3], Circle[\{2,1\}, 0.3], \\
\phantom{In[9]:}Point[\{\{0,0\}, \{2,1\}\}]\}], \\
\phantom{In[}Graphics[\{Arrowheads[\{-.1, .2\}], Arrow[\{\{0,0\}, \{2,1\}\}, .3], \\
\phantom{In[9]:}Circle[\{0,0\}, 0.3], Circle[\{2,1\}, 0.3], \\
\phantom{In[9]:}Point[\{\{0,0\}, \{2,1\}\}]\}], \\
\phantom{In[}Graphics[\{Arrowheads[\{-0.1, -.05, .05, .1\}], \\
\phantom{In[9]:}Arrow[\{\{0,0\}, \{2,1\}\}, \{.3, .1\}], Circle[\{0,0\},\0.3], \\
\phantom{In[9]:}Circle[\{2,1\}, .3], Point[\{\{0,0\}, \{2,1\}\}]\}]\}](/sites/default/files/tex_cache/089d83ff4d005864e7fd398782d54da0.png)
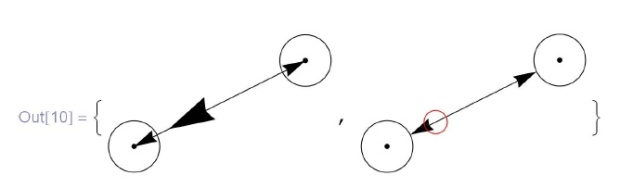
Элемент списка директивы сам может быть списком, второй элемент которого отвечает за относительное положение стрелки (число от нуля до единицы), а третий - за форму (
):
![\tt
In[10]:= \\ \\
\phantom{In}\{Graphics[\{Arrowheads[\{\{-.1, 0\}, \{-.2, 2\}, .1\}], \\
\phantom{In[10]}Arrow[\{\{0,0\}, \{2,1\}\}], Circle[\{0,0\}, 0.3], \\
\phantom{In[10]}Circle[\{2,1\}, 0.3], Point[\{\{0,0\}, \{2,1\}\}]\}], \\
\phantom{In}Graphics[ \\
\phantom{In[10}\{Arrowheads[\{\{-.1, 0\}, \{-.05, .2, Graphics [\{Red, Circle[]\}]\}, \\
\phantom{In[10]:r}.1\}], Arrow[\{\{0,0\}, \{2,1\}\}, .3], Circle[\{0,0\}, 0.3], \\
\phantom{In[10]}Circle[\{2,1\}, 0.3], Point[\{\{0,0\}, \{2,1\}\}]\}]\}](/sites/default/files/tex_cache/cd1b50265804f1944887865af0c29444.png)
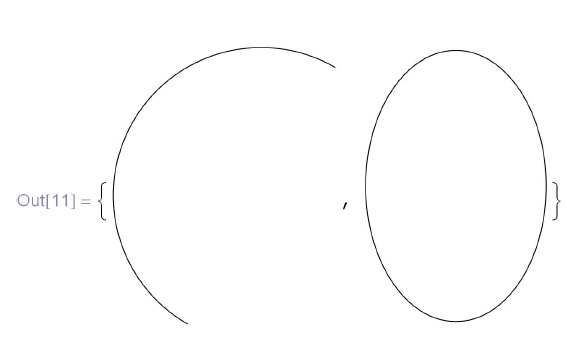
2. Примитив 
может быть использован также для рисования дуг (третий аргумент задает начало и конец дуги в радианах) и эллипсов (второй аргумент в этом случае не радиус, а список длин полуосей). Примитив ![\text{\tt Cycle[]}](/sites/default/files/tex_cache/f827735982398f1ae746b234d319b4f1.png)
без аргументов дает единичную окружность с центром в начале координат:
![\tt
In[11]:=\{Graphics[Circle[\{0, 0\}, 1, \{$\pi$/3, 4$\pi$/3\}]], \\
\phantom{In[11]:=\{}Graphics[Circle[\{0, 0\}, \{2, 3\}]]\}](/sites/default/files/tex_cache/f0cb4282cc5ef1ad30fd4874395c92e9.png)
В качестве примера рассмотрим процедуру, изображающую отрезок прямой в геометрии Лобачевского в круге Пуанкаре:
![\tt
In[12]:= \\ \\
\phantom{In}Inv[a\_] :=a/a.a; (* Инверсия *) \\
\phantom{InMe}Mediatr[a\_, b\_] := \\
\phantom{InMe}Module[\{m, n\}, (* Серединный перпендикуляр к отрезку *) \\
\phantom{InMeM}m=$\frac{a+b}{2}$; n = \{b[\!\![1]\!\!] - a[\!\![l]\!\!] , b[\!\![2]\!\!] - a[\!\![2]\!\!]\}; \\
\phantom{InMeM}(х-m[\!\![l]\!\!]) n[\!\![l]\!\!] + (y-m[\!\![2]\!\!]) n[\!\![2]\!\!] == 0 \\
\phantom{InMe}]; \\
\phantom{In}ATan[x\_, y\_] := If [x == 0, If [y>0, -$\frac{\pi}{2}$, $\frac{\pi}{2}$], ArcTan[$\frac{y}{x}$]]; \\
\phantom{In}(* Удобный арктангенс*)](/sites/default/files/tex_cache/daa0e856e5e87e4bb26c75835c4874bd.png)
![\tt
\phantom{In}LSeg[a\_, b\_] := Module [\{dt, ia, o, r, eql, eq2, res, d, $\alpha$, ax, $\varphi$\},\\
\phantom{InLSe}dt = a[\!\![l]\!\!] b[\!\![2]\!\!] - a[\!\![2]\!\!]b[\!\![l]\!\!];\\
\phantom{InLSe}If[Abs[dt] < $10^{-10}$, Line [\{a, b\}],\\
\phantom{InLSeI}ia = Inv[a];\\
\phantom{InLSeI}eql = Mediatr[a, b];\\
\phantom{InLSeI}eq2 = Mediatr[b, ia];\\
\phantom{InLSeI}res = Solve [\{eql, eq2\}, \{x, y\}] // Flatten;\\
\phantom{InLSeI}о = \{x, y\} /. res;\\
\phantom{InLSeI}r = $\sqrt{(o-a).(o-a)}$;\\
\phantom{InLSeI}d = $\sqrt{(b-a).(b-a)}$;\\
\phantom{InLSeI}$\alpha$ = ArcSin $\left[\frac{d}{2r}\right]$;\\
\phantom{InLSeI}ах = о - $\frac{a+b}{2}$;\\
\phantom{InLSeI}If[ax[\!\![1]\!\!] $\le$ 0, $\varphi$ = ATan[ax[\!\![1]\!\!], ax[\!\![2]\!\!]],\\
\phantom{InLSeII}$\varphi$ = $\pi$ + ATan[ax[\!\![l]\!\!], ax[\!\![2]\!\!]]];\\
\phantom{InLSeI}Circle[o, r, \{$\varphi$ - $\alpha$, $\varphi$ + $\alpha$\}]\\
\phantom{InLSe}]\\
\phantom{InLS}];](/sites/default/files/tex_cache/f5479fc81884ef2ed996854140c9f8ba.png)
![\tt
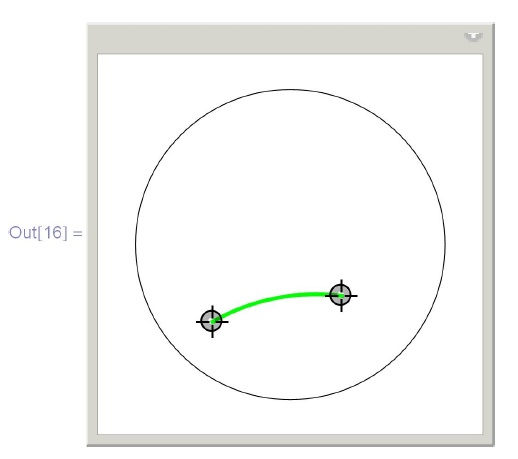
\phantom{In}Manipulate[ \\
\phantom{InM}Graphics[\{Circle[], \{Thick, Green, LSeg[p[\!\![1]\!\!], p[\!\![2]\!\!]]\}\}], \\
\phantom{InM}\{\{p, \{\{-1/2, -1/2\}, \{1/3, -1/3\}\}\}, Locator\}]](/sites/default/files/tex_cache/5104370ec4bcf62954524b016860d548.png)
3. Аналогичные модификации имеются у примитива 
:
![\tt
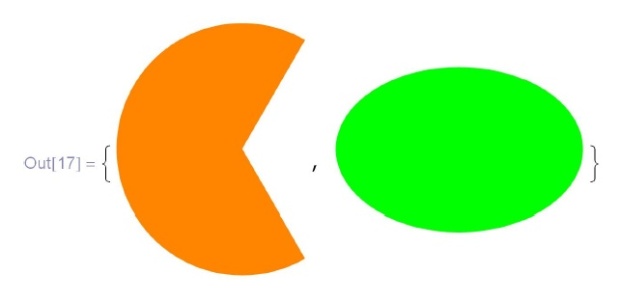
In[17]:=\{Graphics [\{Orange, Disk [\{0, 0\}, 1, \{$\pi$/3, 5$\pi$/3\}]\}], \\
\phantom{In[17]:=\{}Graphics[\{Green, Disk[\{0, 0\}, \{3, 2\}]\}]\}](/sites/default/files/tex_cache/da6741305cf948894f5512d5b7a2035e.png)
4. Примитив 
позволяет рисовать сразу несколько ломаных, например, две ломаные, отличающиеся на параллельный перенос на вектор 
:
![\tt
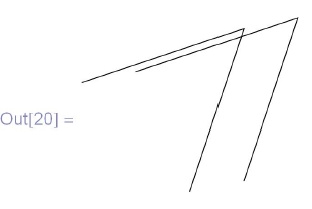
In[18]:=11=\{\{1,0\}, \{2,3\}, \{-1,2\}\}; \\
\phantom{In[18]:=}a={1, .2}; \\
\phantom{In[18]:=}Graphics[Line[\{11, Map[a+\#&, 11]\}]]](/sites/default/files/tex_cache/0693be4cd1ed2cc1bbc9cae2bbf905c4.png)
5. Точно так же 
может рисовать сразу несколько многоугольников. Кроме того, цвет многоугольника можно задавать "от вершин, по градиенту". Для этого используется опция 
.
![\tt
In[21]:= \\
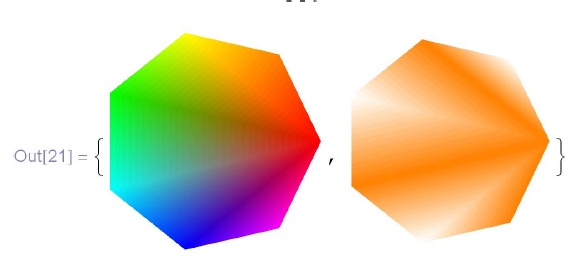
\phantom{In}\{Graphics[Polygon[Table[\{Cos[i $\frac{2\pi}{7}$], Sin[i $\frac{2\pi}{7}$]\}, \{i, 0, 6\}], \\
\phantom{In\{Gr}VertexColors$\to$\{Red, Orange, Yellow, Green, Cyan, Blue, \\
\phantom{In\{GrVe}Magenta\}]], \\
\phantom{In\{}Graphics[Polygon[Table[\{Cos[i $\frac{2\pi}{7}$], Sin[i $\frac{2\pi}{7}$]\}, \{i, 0, 6\}], \\
\phantom{In\{Gr}VertexColors$\to$\{Orange, White, Orange, White, Orange, \\
\phantom{In\{GrVe}White, Orange\}]]\}](/sites/default/files/tex_cache/d2dd722959e18e9546ef53c07c4c7cef.png)
6.Если примитив 
использовать с одним аргументом, то получится единичный квадрат с заданным левым нижним углом. Если вовсе без аргументов - то с левым нижним углом в начале координат.
7.Наконец, примитив 
располагает средствами для позиционирования текста (второй аргумент), выбора отступа (третий аргумент), направления (четвертый), фона (пятый) и т. п. Мы не будем на этом останавливаться подробно, приведем только один пример:
![\tt
In[22]:=Graphics[\\
\phantom{In[22]:=G}\{Circle[], Text["Это окружность"\ \!\!\!\!, \{0,0\}, Automatic,\\
\phantom{In[22]:=Gra}\{1,1\}, Background $\to$ LightRed],\\
\phantom{In[22]:=Gr}Text[Style[x\^\,\!2+y\^\,\!2==1, 15, Bold], \{1/2,0\},\\
\phantom{In[22]:=Gra}FormatType $\to$ TraditionalForm]\}]](/sites/default/files/tex_cache/a2ce110bbcd013d2cf3455a169c60194.png)
Прежде чем перейти к полному списку графических директив, перечислим оставшиеся примитивы:
8. Примитив 
, служащий для вставки одного объекта внутрь другого, например, подписи к рисункам.
9. Примитив 
, изображающий прямоугольник, разбитый на раскрашенные квадратики заданных цветов.
10. Примитив 
служит для создания динамического элемента графики, позволяющего вводить координаты текущей точки экрана.
11. Примитив 
служит для объединения объектов в группу, которая может быть отредактирована как единое целое.
12. Примитив 
- важный элемент графики, позволяющий отдельно задавать структуру одномерного, двумерного или трехмерного комплекса (набора примитивов), и отдельно задавать координаты определяющих их точек: ![\text{\tt GraphicsComplex[координаты вершин, структура]}](/sites/default/files/tex_cache/c0c0736da3bc6bc1d678aaca7e742e67.png)
. В структуре вершины задаются уже только своими номерами в списке вершин. Приведем пример. Здесь список вершин состоит из 6 элементов (первые три - вершины треугольника, оставшиеся три - середины его сторон):
![\tt
In[23]:=
\phantom{In}a=\{-1,-1\}; b=\{1,-1\}; c=\{0,1\}; \\
\phantom{In}v=\{a,b,c\}$\sim$Join$\sim$\{$\frac{b+c}{2}$, $\frac{a+c}{2}$, $\frac{b+a}{2}$\}\\
\phantom{In}Graphics[GraphicsComplex[v, \\
\phantom{InGr}\{Thin, Line[\{1, 2, 3, 1\}], Green, Thick, Line [\{1, 4\}],\\
\phantom{InGra}Line[\{2, 5\}], Line [\{3, 6\}], Red, PointSize[Large],\\
\phantom{InGra}Point[\{1,2,3\}], Blue, PointSize [Medium], Point[\{4,5,6\}]\}]]](/sites/default/files/tex_cache/81ae6fb7712c0ef17a8096242c256ac1.png)
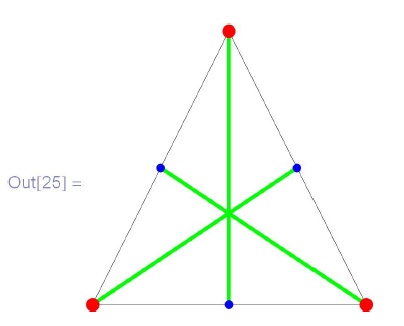
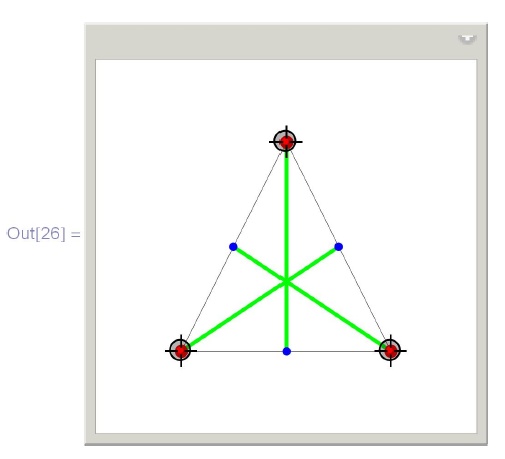
Это удобно, например, при создании динамических объектов. Скажем, вот иллюстрация к теореме о том, что медианы треугольника пересекаются в одной точке (в 
координаты трех точек из списка a задаются с помощью примитива , дающего возможность вводить положение точки мышью):
![\tt
In[26]:=Manipulate[\\
\phantom{In[26]:=M}Graphics[GraphicsComplex[\\
\phantom{In[26]:=Man}a$\sim$Join$\sim$$\left\{\frac{a[[2]]+a[[3]]}{2},\, \frac{a[[1]]+a[[3]]}{2},\, \frac{a[[2]]+a[[1]]}{2}\right\}$,\\
\phantom{In[26]:=Man}\{Thin, Line[\{1,2,3,1\}], Green, Thick, Line[\{1,4\}],\\
\phantom{In[26]:=Mani}Line[\{2, 5\}], Line[\{3, 6\}], Red, PointSize[Large],\\
\phantom{In[26]:=Mani}Point[\{1, 2, 3\}], Blue, PointSize[Medium],\\
\phantom{In[26]:=Mani}Point[\{4, 5, 6\}]\}], PlotRange$\to$1.5],\\
\phantom{In[26]:=M}\{\{a,\{\{-1, -1\}, \{1, -1\}, \{0, 1\}\}\},Locator\}]](/sites/default/files/tex_cache/b10b39b3d168ff8d544091740b38a724.png)
