| Узбекистан, Республика Каракалпакистан, район Елликкала |
Диспетчирование параллельных вычислительных систем
Диспетчер последовательного назначения для неоднородной ВС
В основе диспетчера лежит следующее решающее правило:
Введем сквозную нумерацию процессоров от 1 до 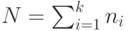 . Зададим вес {tj1 ... tjN} j -й вершины (j = 1 ... m; m
— размер матрицы S или объем буфера диспетчера)
так, что при новой нумерации процессоров tjl — время
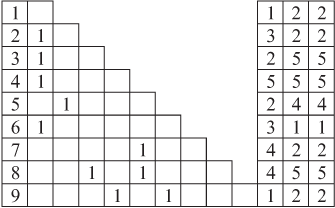
выполнения j -й работы l -м процессором. Например, при k = 2, n1 = 1, n2 =
2 расширенная матрица
следования на рис. 10.15б примет вид,
представленный на рис. 10.16.
. Зададим вес {tj1 ... tjN} j -й вершины (j = 1 ... m; m
— размер матрицы S или объем буфера диспетчера)
так, что при новой нумерации процессоров tjl — время
выполнения j -й работы l -м процессором. Например, при k = 2, n1 = 1, n2 =
2 расширенная матрица
следования на рис. 10.15б примет вид,
представленный на рис. 10.16.
В процессе распределения работ будем формировать расписание в виде таблицы 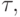 состоящей из N строк, каждая из которых соответствует одному
процессору. В
строке будем записывать последовательность заданий одному процессору. Задания
имеют два вида: выполнить работу
состоящей из N строк, каждая из которых соответствует одному
процессору. В
строке будем записывать последовательность заданий одному процессору. Задания
имеют два вида: выполнить работу 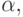 простоять t
единиц времени
(изображается
простоять t
единиц времени
(изображается 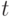 ). Момент Ti , i = 1 ...
N, окончания (отсчет ведется
от нуля) выполнения последней работы или простоя, назначенных к данному моменту
распределения i -му процессору, назовем текущим временем занятости
процессора.
). Момент Ti , i = 1 ...
N, окончания (отсчет ведется
от нуля) выполнения последней работы или простоя, назначенных к данному моменту
распределения i -му процессору, назовем текущим временем занятости
процессора.
В процессе распределения и имитации выполнения работ будем использовать
множество A номеров работ, уже назначенных на процессоры, но не
выполненных в анализируемый момент времени. A представляет собой
таблицу, содержащую пары "назначенная для выполнения задача — время
окончания ее выполнения ", т.е. 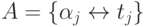 .
.
Множество R — множество работ, соответствующих не назначенным входам (нулевым строкам) текущего значения изменяемой матрицы следования S.
- Полагаем первоначально
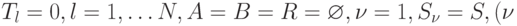 — номер шага распределения). Переходим к выполнению 5.
— номер шага распределения). Переходим к выполнению 5. - Находим в множестве A значение tmu = minj
{ti} и множество
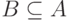 номеров работ,
назначенных на процессоры и закончивших выполнение к моменту
номеров работ,
назначенных на процессоры и закончивших выполнение к моменту 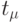 . Полагаем
равными нулю все позиции A, составляющие B. Этим
имитируется окончание выполнения
работ на процессорах к моменту времени
. Полагаем
равными нулю все позиции A, составляющие B. Этим
имитируется окончание выполнения
работ на процессорах к моменту времени 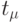 .
. - Для всех процессоров, для которых текущее время занятости меньше значения
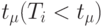 , записываем простой в течение времени
, записываем простой в течение времени  (символом простоя
(символом простоя  ). Для этих процессоров полагаем
). Для этих процессоров полагаем  .
. - Исключаем из
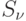 строки и столбцы, соответствующие
всем работам из B,
после чего матрицу
строки и столбцы, соответствующие
всем работам из B,
после чего матрицу  уплотним. Полагаем
уплотним. Полагаем 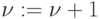 . Таким образом
сформируется матрица
. Таким образом
сформируется матрица 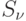 (а также
(а также 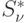 ) на
новом шаге распределения.
) на
новом шаге распределения. - Находим множество R — входов матрицы следования
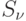 , соответствующих не
назначенным ранее работам. Если
, соответствующих не
назначенным ранее работам. Если  , переходим к
выполнению 6, в противном
случае выполняем пункт 2.
, переходим к
выполнению 6, в противном
случае выполняем пункт 2. - Пусть для определенности
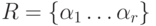 ,
работе
,
работе 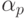 соответствует вес {tp1 ... tpN}, p = 1 ... r. Формируем суммы Tl + tpl , l = 1 ... N,
p = 1 ... r. Для каждого значения p (т.е. для каждой
работы из R ) находим
минимальную (по l ) из таких сумм, т.е. для каждой работы находим
один или
несколько процессоров, на которых время окончания выполнения этой работы
минимально
при текущих значениях занятости процессоров. Найденные суммы сведем в
невозрастающую последовательность R*, состоящую из r чисел. При этом сохраним
информацию о соответствии процессорам.
соответствует вес {tp1 ... tpN}, p = 1 ... r. Формируем суммы Tl + tpl , l = 1 ... N,
p = 1 ... r. Для каждого значения p (т.е. для каждой
работы из R ) находим
минимальную (по l ) из таких сумм, т.е. для каждой работы находим
один или
несколько процессоров, на которых время окончания выполнения этой работы
минимально
при текущих значениях занятости процессоров. Найденные суммы сведем в
невозрастающую последовательность R*, состоящую из r чисел. При этом сохраним
информацию о соответствии процессорам. - Ставим в соответствие каждой p -й работе, представленной в
последовательности R*, значение
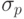 , равное числу процессоров,
при выполнении на которых достигается
найденное минимальное время окончания выполнения этой работы.
, равное числу процессоров,
при выполнении на которых достигается
найденное минимальное время окончания выполнения этой работы. - Производим последовательное назначение работ на процессоры следующим
образом.
Назначаем не более N работ слева направо в соответствии с
вхождением времени
окончания их выполнения в последовательность R*. Каждую p -ю работу назначаем на
все те процессоры, (их число равно
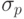 ), на которых
достигается входящее в R* время окончания выполнения. В результате те работы, для
которых
), на которых
достигается входящее в R* время окончания выполнения. В результате те работы, для
которых  , окажутся
назначенными более чем на один процессор, а на один процессор на данном шаге
могут оказаться назначенными более одной работы. Чтобы определить окончательно,
на какой процессор должна быть назначена p -я работа,
воспользуемся следующей процедурой. Для каждого
процессора проводим анализ, сколько работ назначено
на него на данном шаге распределения. Если назначения не произошло, переходим
к анализу назначения на следующий процессор или заканчиваем анализ процессоров,
если все они просмотрены. Если оказалась назначенной на процессор одна, p -я,
работа, считаем ее окончательно закрепленной за данным процессором, и, если
, окажутся
назначенными более чем на один процессор, а на один процессор на данном шаге
могут оказаться назначенными более одной работы. Чтобы определить окончательно,
на какой процессор должна быть назначена p -я работа,
воспользуемся следующей процедурой. Для каждого
процессора проводим анализ, сколько работ назначено
на него на данном шаге распределения. Если назначения не произошло, переходим
к анализу назначения на следующий процессор или заканчиваем анализ процессоров,
если все они просмотрены. Если оказалась назначенной на процессор одна, p -я,
работа, считаем ее окончательно закрепленной за данным процессором, и, если 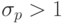 , исключаем ее из рассмотрения при анализе
последующих процессоров — т.е.,
снимаем ее с назначения на другие процессоры. Если на процессор назначено
более
одной работы, закрепляем за процессором лишь ту работу
, исключаем ее из рассмотрения при анализе
последующих процессоров — т.е.,
снимаем ее с назначения на другие процессоры. Если на процессор назначено
более
одной работы, закрепляем за процессором лишь ту работу 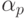 ,
которая имеет
минимальное значение
,
которая имеет
минимальное значение 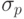 . Если несколько работ имеют равное
минимальное значение
. Если несколько работ имеют равное
минимальное значение 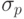 , назначаем любую (первую) из них. Для множества работ
, назначаем любую (первую) из них. Для множества работ 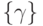 , отклоненных от
назначения на данный процессор, полагаем
, отклоненных от
назначения на данный процессор, полагаем 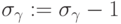 . Значение
. Значение 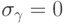 означает,
что работе
означает,
что работе  отказано в назначении на данном шаге
распределения. Назначенную
работу исключаем из рассмотрения при анализе следующих процессоров. Номера
назначенных работ оказываются записанными в строки таблицы
отказано в назначении на данном шаге
распределения. Назначенную
работу исключаем из рассмотрения при анализе следующих процессоров. Номера
назначенных работ оказываются записанными в строки таблицы 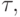 соответствующие
процессорам. Эти номера исключаем из R. Номер каждой назначенной
работы и время
окончания ее выполнения (оно же — время занятости процессора) заносим в A.
соответствующие
процессорам. Эти номера исключаем из R. Номер каждой назначенной
работы и время
окончания ее выполнения (оно же — время занятости процессора) заносим в A. - Проверяем, все ли работы распределены. При отрицательном результате
проверки
переходим к выполнению 2.
Конец алгоритма.
При k = 2, n1 = 1, n2 = 2, (N = 3) распределим работы, отображенные расширенной матрицей следования на рис. 10.16 (соответствующей графу на рис. 10.15), для минимизации времени выполнения.
-
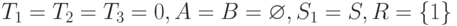 . Выполнение работы 1 ранее
всех закончит процессор 1. После ее назначения
. Выполнение работы 1 ранее
всех закончит процессор 1. После ее назначения  .
. - Найдем в A работу 1 с минимальным временем окончания
выполнения, равным 1.
Записываем простои в одну единицу времени процессорам 2 и 3. Таблица
 принимает вид
принимает вид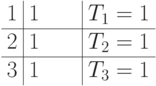
-
После исключения первой строки и первого столбца из S1 (т.е. по матрице S2 ) найдем R = {2, 3, 4, 6}. Составим таблицу 10.1 времени окончания выполнения каждой работы из R каждым процессором l = 1, 2, 3. Минимальное время окончания выполнения каждой работы выделено.
Формируем последовательность
 ,
, 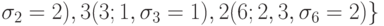 ,
где в круглых скобках указаны номер работы, список процессоров, на которых
достигается минимальное время окончания ее выполнения, и число
,
где в круглых скобках указаны номер работы, список процессоров, на которых
достигается минимальное время окончания ее выполнения, и число 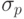 этих процессоров.
этих процессоров.Назначим первоначально (таблица 10.2) работу 4 на процессоры 1, 2, 3, работу 2 — на процессоры 2 и 3 , работу 3 — на процессор 1.
После анализа значений
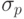 оставим на процессоре 1
работу 3 (после чего
оставим на процессоре 1
работу 3 (после чего 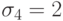 ), на процессоре 2 — работу 4 (после чего
), на процессоре 2 — работу 4 (после чего 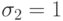 ), на процессоре 3
— работу 2,
), на процессоре 3
— работу 2, 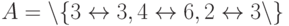 .
Таблица распределения
.
Таблица распределения  примет вид
примет вид
-
B = {2, 3}. После исключения строк и столбцов, соответствующих работам 2 и 3, из матрицы S2, т.е. по сформированной матрице S3, найдем R = {5, 6}. Составим таблица 10.3 значений времени окончания выполнения каждой работы из R каждым процессором.
Из таблицы найдем
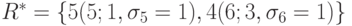 ,
,Назначим работу 5 на процессор 1, работу 6 — на процессор 3,
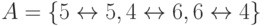 .
Таблица распределения
.
Таблица распределения  примет вид
примет вид
-
B = {6}. После исключения строки и столбца, соответствующих работе 6, из матрицы следования S3, т.е. по сформированной матрице S4, найдем
 .
Назначим процессору 3 простой в течение одной условной единицы времени.
Таблица
.
Назначим процессору 3 простой в течение одной условной единицы времени.
Таблица  примет вид
примет вид
-
B = {5}. После преобразования матрицы S4, т.е. по матрице S5, найдем R = {7, 8}. Из таблицы 10.4, аналогичной таблице 3, найдем
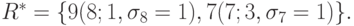
Назначаем работу 8 на процессор 1, работу 7 — на процессор 3. Таблица
 примет вид
примет вид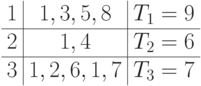
-
B = {4}. После исключения строки и столбца, соответствующих работе 4, из матрицы следования S5, т.е. по сформированной при этом матрице S6, найдем R = {9}. Время окончания выполнения работы 9 на процессорах равно соответственно 10, 8, 9. Назначаем работу 9 на процессор 2. Таблица
 примет окончательный вид
примет окончательный вид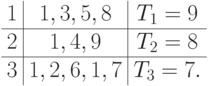
Данный диспетчер для неоднородной ВС построен на основе обобщения рассмотренного диспетчера последовательного назначения для однородных ВС, который можно рассматривать как частный случай при k = 1.
Он применим и в другом частном случае: когда отсутствует частичная упорядоченность работ, то есть когда надо разделить "поровну" взаимно независимые работы между n исполнителями. Наглядный пример такого распределения составляет задача о рюкзаках, рассмотренная в разделе 10.1.1.

 4 = 3), 3(
4 = 3), 3(