Алгоритмы обучения

Обучение персептрона

В 1957 г. Р.Розенблатт разработал модель, которая вызвала большой интерес у исследователей. Несмотря на некоторые ограничения ее исходной формы, она стала основой для многих современных, наиболее сложных алгоритмов обучения с учителем.

Персептрон является двухуровневой нерекуррентной сетью, вид которой показан на рис. 15.3. Она использует алгоритм обучения с учителем ; другими словами, обучающая выборка состоит из множества входных векторов, для каждого из которых указан свой требуемый вектор цели. Компоненты входного вектора представлены непрерывным диапазоном значений; компоненты вектора цели являются двоичными величинами (0 или 1). После обучения сеть получает на входе набор непрерывных входов и вырабатывает требуемый выход в виде вектора с бинарными компонентами.

Рис. 15.3.

Обучение осуществляется следующим образом:

1. Рандомизируются все веса сети в малые величины.

2. На вход сети подается входной обучающий вектор и вычисляется сигнал NET от каждого нейрона, используя стандартное выражение

   

3. Вычисляется значение пороговой функции активации для сигнала NET от каждого нейрона следующим образом:

   

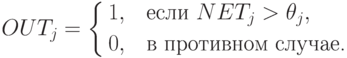
   Здесь 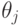представляет собой порог, соответствующий нейрону (в простейшем случае все нейроны имеют один и тот же порог).

4. Вычисляется ошибка для каждого нейрона посредством вычитания полученного выхода из требуемого выхода:

   

5. Каждый вес модифицируется следующим образом:

   
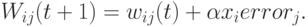
6. Повторяются шаги со второго по пятый до тех пор, пока ошибка не станет достаточно малой.

Метод обучения Уидроу—Хоффа

Как мы видели, персептрон ограничивается бинарными выходами. Б.Уидроу вместе со студентом университета М.Хоффом расширили алгоритм обучения персептрона для случая непрерывных выходов, используя сигмоидальную функцию. Второй их впечатляющий результат — разработка математического доказательства, что сеть при определенных условиях будет сходиться к любой функции, которую она может представить. Их первая модель — Адалин — имеет один выходной нейрон, более поздняя модель — Мадалин — расширяет ее для случая с многими выходными нейронами.

Выражения, описывающие процесс обучения Адалина, очень схожи с персептронными. Существенные отличия имеются в четвертом шаге, где используются непрерывные сигналы NET вместо бинарных OUT. Модифицированный шаг 4 в этом случае реализуется следующим образом:

4. Вычисляется ошибка для каждого нейрона посредством вычитания полученного выхода из требуемого выхода: