| Россия |
Когнитрон
Обучение когнитрона
Так как когнитрон реализован в виде многослойной сети, возникают сложные проблемы обучения, связанные с выбранной структурой. Получая обучающий набор входных образов, сеть самоорганизуется посредством изменения силы синаптических связей. При этом отсутствуют предварительно определенные выходные образы, представляющие требуемую реакцию сети, однако сеть самонастраивается с целью распознавания входных образов с замечательной точностью.
Алгоритм обучения когнитрона является концептуально привлекательным. В заданной области слоя обучается только наиболее сильно возбужденный нейрон. Автор сравнивает это с "элитным обучением", при котором обучаются только "умные" элементы. Те нейроны, которые уже хорошо обучены, что выражается силой их возбуждения, получат приращение силы своих синапсов с целью дальнейшего усиления своего возбуждения.
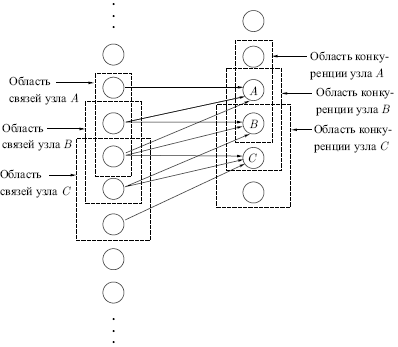
На рис. 13.2 показано, что области связи соседних узлов значительно перекрываются. Такое расточительное дублирование функций оправдывается взаимной конкуренцией между ближайшими узлами. Даже если узлы в начальный момент имеют абсолютно идентичный выход, небольшие отклонения всегда случаются; один из узлов всегда будет иметь более сильную реакцию на входной образ, чем соседние. Его сильное возбуждение будет оказывать сдерживающее воздействие на возбуждение соседних узлов, и усиливаться будут только его синапсы — синапсы соседних узлов останутся неизменными.
Возбуждающий нейрон. Можно сказать, что выход возбуждающего нейрона в когнитроне определяется отношением его возбуждающих входов к тормозящим входам. Эта необычная функция имеет важные преимущества, как практические, так и теоретические. Суммарный возбуждающий вход в нейрон является взвешенной суммой входов от возбуждающих входов в предшествующем слое. Аналогично суммарный вход является взвешенной суммой входов от всех тормозящих нейронов. В символьном виде
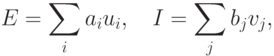
где  — вес
— вес  -го возбуждающего синапса,
-го возбуждающего синапса, 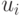 — выход
— выход  -го
возбуждающего нейрона,
-го
возбуждающего нейрона, 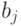 — вес
— вес  -го тормозящего
синапса,
-го тормозящего
синапса, 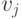 —
выход
—
выход  -го тормозящего нейрона.
-го тормозящего нейрона.
Заметим, что веса имеют только положительные значения. Выход нейрона затем вычисляется следующим образом:
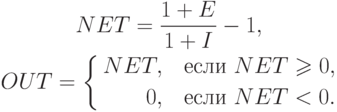
Предполагая, что NET имеет положительное значение, можно записать:
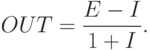
Когда тормозящий вход мал (  ), OUT может быть
аппроксимировано как
), OUT может быть
аппроксимировано как
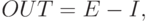
что соответствует выражению для обычного линейного порогового элемента (с нулевым порогом).