Обобщения и применения модели Хопфилда

Приложения

Аналого-цифровой преобразователь

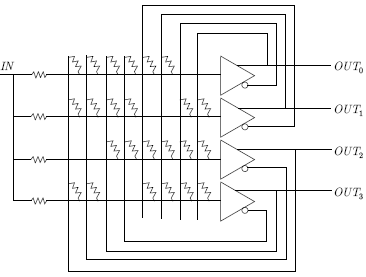
Рассмотрим электрическую схему, которая основана на сети с обратной связью и реализует четырехбитовый аналого-цифровой преобразователь. На рис. 9.2 показана блок-схема этого устройства с усилителями, выполняющими роль искусственных нейронов. Сопротивления, выполняющие роль весов, соединяют выход каждого нейрона с входами всех остальных. Чтобы удовлетворить условию устойчивости, выход нейрона не соединялся сопротивлением с его собственным входом, а веса брались симметричными, т. е. сопротивление от выхода нейрона к входу нейрона имело ту же величину, что и сопротивление от выхода нейрона к входу нейрона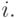

Заметим, что усилители имеют прямой и инвертированный выходы. Это позволяет с помощью обычных положительных сопротивлений реализовывать и те случаи, когда веса должны быть отрицательными. На рис. 9.2 показаны все возможные сопротивления, при этом никогда не возникает необходимости присоединять как прямой, так и инвертированный выходы нейрона к входу другого нейрона.

Рис. 9.2.

В реальной системе каждый усилитель обладает конечным входным сопротивлением и входной емкостью, что должно учитываться при расчете динамических характеристик. Для устойчивости сети не требуется равенства этих параметров для всех усилителей и их симметричности. Так как эти параметры влияют лишь на затраченное для получения решения время, а не на само решение, для упрощения анализа они исключены.

Предполагается, что используется пороговая функция (предел сигмоидальной функции при , стремящемся к бесконечности). Далее, все выходы изменяются в начале дискретных интервалов времени, называемых эпохами. В начале каждой эпохи исследуется сумма входов каждого нейрона. Если она больше порога, выход принимает единичное значение, если меньше — нулевое. На протяжении эпохи выходы нейронов не изменяются.

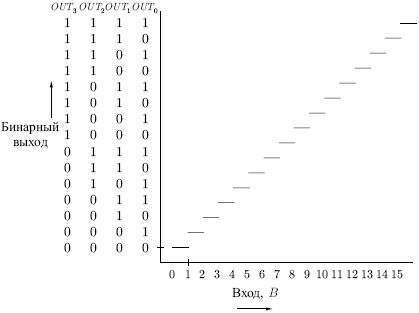
Целью является такой выбор сопротивлений (весов), чтобы непрерывно растущее напряжение , приложенное к одновходовому терминалу, порождало множество из четырех выходов, представляющих двоичную запись числа, величина которого приближенно равна входному напряжению (см. рис. 9.3). Определим сначала функцию энергии следующим образом:

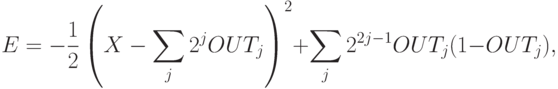
где — входное напряжение.

Когда минимизировано, то получаются нужные выходы. Первое выражение в скобках минимизируется, когда двоичное число, образованное выходами, наиболее близко (в среднеквадратичном смысле) к аналоговой величине входа 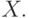Второе выражение в скобках обращается в нуль, когда все выходы равны 1 или 0, тем самым накладывая ограничение, что выходы принимают только двоичные значения.

Если данное уравнение перегруппировать, то получим следующее выражение для весов:

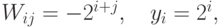
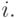где — проводимость (величина, обратная сопротивлению) от выхода нейрона к входу нейрона (равная также проводимости от выхода нейрона к входу нейрона ); — проводимость от входа к входу нейрона Чтобы получить схему с приемлемыми значениями сопротивлений и потребляемой мощности, все веса должны быть промасштабированы.

Рис. 9.3.

Идеальная выходная характеристика, изображенная на рис. 9.3, будет реализована лишь в том случае, если входы устанавливаются в нуль перед выполнением преобразования. Если этого не делать, сеть может попасть в локальный минимум энергии и дать неверный выход.