Сети встречного распространения

Обучение слоя Гроссберга

Слой Гроссберга обучается относительно просто. Входной вектор, являющийся выходом слоя Кохонена, подается на слой нейронов Гроссберга, и выходы слоя Гроссберга вычисляются как при нормальном функционировании. Далее, каждый вес корректируется только в том случае, если он соединен с нейроном Кохонена, имеющим ненулевой выход. Величина коррекции веса пропорциональна разности между весом и требуемым выходом нейрона Гроссберга, с которым этот вес соединен. В символьной записи

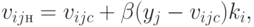
где 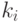— выход -го нейрона Кохонена (только для одного нейрона Кохонена он отличен от нуля); — -я компонента вектора желаемых выходов.

Первоначально берется равным приблизительно 0,1 и затем постепенно уменьшается в процессе обучения.

Отсюда видно, что веса слоя Гроссберга будут сходиться к средним величинам от желаемых выходов, тогда как веса слоя Кохонена обучаются на средних значениях входов. Обучение слоя Гроссберга — это обучение с учителем, алгоритм располагает желаемым выходом, по которому он обучается. Обучающийся без учителя, самоорганизующийся слой Кохонена дает выходы в недетерминированных позициях. Они отображаются в желаемые выходы слоем Гроссберга.

Сеть встречного распространения полностью

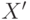На рис. 6.7 показана сеть встречного распространения целиком. В режиме нормального функционирования предъявляются входные векторы и , и обученная сеть дает на выходе векторы и 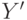, являющиеся аппроксимациями соответственно для и 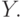Векторы и предполагаются здесь нормализованными единичными векторами, следовательно, порождаемые на выходе векторы также будут иметь тенденцию быть нормализованными.

Рис. 6.7.

В процессе обучения векторы и подаются одновременно и как входные векторы сети, и как желаемые выходные сигналы. Вектор используется для обучения выходов 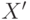, а вектор — для обучения выходов 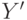слоя Гроссберга. Сеть встречного распространения целиком обучается с использованием того же самого метода, который описывался для сети прямого действия. 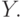Нейроны Кохонена принимают входные сигналы как от векторов , так и от векторов Но эта ситуация неотличима от той, когда имеется один большой вектор, составленный из векторов и , и тем самым не влияет на алгоритм обучения.

В качестве результирующего получается единичное отображение, при котором предъявление пары входных векторов порождает их копии на выходе. Этот вывод не представляется особенно интересным, если не заметить, что предъявление только вектора (с вектором , равным нулю) порождает как выходы 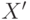, так и выходы 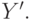Если — функция, отображающая в 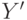, то сеть аппроксимирует ее. 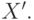Также, если обратима, то предъявление только вектора (приравнивая нулю) порождает Уникальная способность сети встречного распространения — порождать функцию и обратную к ней — делает эту сеть полезной в ряде приложений.

Рис. 6.7, в отличие от первоначальной конфигурации, не демонстрирует противоток в сети, по которому она получила свое название. Такая форма выбрана потому, что она также иллюстрирует сеть без обратных связей и позволяет обобщить понятия, развитые в предыдущих лекциях.