НОУ ИНТУИТ | Основы теории вычислимых функций. Лекция 11: Рекурсивные функции

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 16.03.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 5 студентам

| Поделиться |

Поддержать программу

Оценки скорости роста. Функция Аккермана

Обратимся теперь к вопросу, который можно было бы задать уже давно: существуют ли общерекурсивные, но не примитивно рекурсивные функции? Мы приведем два доказательства существования таковых. Первое исходит из общих соображений:

Теорема 81. Существует всюду определенная вычислимая функция двух аргументов, универсальная для класса всех примитивно рекурсивных функций одного аргумента.

Очевидно, что если U такая функция, то функция d, для которой d(n)=U(n,n)+1, будет всюду определенной, вычислимой и будет отличаться от любой примитивно рекурсивной функции (от n -ой в точке n ).

Всякая примитивно рекурсивная функция получается из базисных с помощью некоторой последовательности операций подстановки и рекурсии. Ясно, что такую последовательность можно описать словом в конечном алфавите так сказать, программой (в которой последовательно определяются различные примитивно рекурсивные функции и для каждой написано, из каких других она получается и с помощью каких операций). Из всех программ отберем программы для одноместных функций (разумеется, в качестве промежуточных функций можно использовать функции с любым числом аргументов). Множество таких программ разрешимо, их можно пронумеровать вычислимым образом. Функция 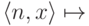$\langle n,x\rangle \hm\mapsto$ (результат применения функции, заданной программой номер n, к числу x ) будет вычислима и по построению будет универсальной для класса примитивно рекурсивных функций.

Однако интересно указать и более конкретную причину, мешающую некоторым вычислимым функциям быть примитивно рекурсивными. Вот одна из возможностей: примитивно рекурсивные функции не могут быстро расти. Эта идея восходит к Аккерману, который построил функцию, растущую быстрее всех примитивно рекурсивных функцию Аккермана. Сейчас мы изложим эту конструкцию (хотя детали построения будут иными).

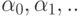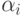Определим последовательность функций $\alpha _{0},\alpha _{1},..$ . от одного аргумента. (Все эти функции будут всюду определенными.) Положим $\alpha _{0}(x)=x+1$ . Определяя $\alpha _{i}$ , мы будем использовать такое обозначение: f^[n](x) означает f(f(...f(x)...)), где функция f использована n раз. Так вот,

$\alpha_{i} (x) = \alpha_{i-1}^{[x+2]}(x)$

(почему удобно применять функцию 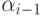$\alpha _{i-1}$ ровно x+2 раза, мы увидим чуть позже).

Очевидные свойства (формально их можно доказать по индукции):

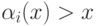$\alpha _{i} (x)>x$ при всех i и x ;
$\alpha _{i} (x)$ возрастает с возрастанием x ;
$\alpha _{i} (x)$ возрастает с возрастанием i (для каждого фиксированного x );
$\alpha _{i} (x) \ge \alpha _{i-1}(\alpha _{i-1}(x))$ .

Теперь можно оценить скорость роста любой примитивно рекурсивной функции.

Теорема 82. Пусть f примитивно рекурсивная функция n аргументов. Тогда найдется такое k, что

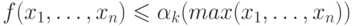
$f(x_{1},\dots ,x_{n}) \le \alpha _{k} (max(x_{1},\dots ,x_{n}))$

при всех x₁,...,x_n.

Идея проста можно оценить скорость роста композиции функций, зная оценки для каждой из них; аналогично для рекурсии. Формально говоря, доказательство использует " индукцию по построению" примитивно рекурсивных функций.

Для базисных функций утверждение очевидно. Посмотрим на подстановку. Пусть

f(x)=g(h₁(x),...,h_k(x))

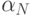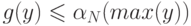(для краткости мы пишем одну букву x, имея в виду вектор переменных). Пусть $\alpha _{N}$ оценивает все функции h₁,...,h_k и функцию g сверху, то есть $h_{i}(x)\le \alpha _{N}(max(x))$ при всех i и x, а также $g(y) \le \alpha _{N}(max(y))$ (здесь max(u) означает максимальный элемент в наборе u ). Тогда f(x) не превосходит

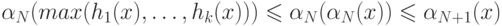
$\alpha _{N}(max(h_{1}(x),\dots ,h_{k}(x))) \le \alpha _{N}(\alpha _{N}(x)) \le \alpha _{N+1}(x)$

(мы пользуемся указанными выше свойствами функций 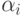$\alpha _{i}$ ).

Похоже (но немного сложнее) дело обстоит с рекурсией. Пусть функция f определяется рекурсивно:

f(x,0)=g(x);
f(x,n+1)=h(x,n,f(x,n)).

(Здесь x также обозначает набор нескольких переменных.) Пусть функции g и h оцениваются сверху функцией 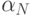$\alpha _{N}$ . Тогда

$f(x,1)=h(x,0,f(x,0)) \le \alpha _{N} (max(x,0,f(x,0))) \le \alpha _{N}(max(x,0,\alpha _{N}(max(x)))) \le \alpha _{N}(\alpha _{N}(max(x)))$

(в последнем переходе мы пользуемся тем, что 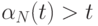$\alpha _{N}(t)>t$ ). Аналогично $f(x,2) \le \alpha _{N}(\alpha _{N}(\alpha _{N}(max(x))))$ и вообще

$f(x,i)\le \alpha_N^{[i+1]}(\max(x))\le \alpha_{N+1}(\max(i,\max(x))),$

что и требовалось доказать.

Заметим, что каждый оператор подстановки или рекурсии увеличивает номер верхней оценки на 1, так что функция, в определении которой не более 100 операторов, растет не быстрее 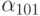$\alpha _{101}$ .

Очевидным следствием полученной оценки является такое утверждение:

Теорема 83. Функция 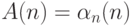$A(n)=\alpha _{n}(n)$ растет быстрее любой примитивно рекурсивной функции.

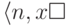
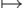
Отметим, что определение функции Аккермана (точнее, функции 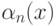$\langle n,x\square$ $\mapsto$ $\alpha _{n}(x)$ ) вполне можно назвать рекурсивным одно значение этой функции определяется через другие, с меньшим первым аргументом. Оно является примером рекурсивного определения, не сводящегося к примитивной рекурсии.

90. Покажите, что прямой пересчет (в возрастающем порядке) бесконечного примитивно рекурсивного множества может не быть примитивно рекурсивной функцией.

91. Покажите, что функция, обратная к примитивно рекурсивной биекции i : N -> N, может не быть примитивно рекурсивной.

92. Покажите, что для любой одноместной примитивно рекурсивной функции h и для любой трехместной примитивно рекурсивной функции g рекурсивное определение

f(x,0)= h(x);
f(x,i+1)= g(x,i, f(2x,i))

задает примитивно рекурсивную функцию.

Дальше >>

Основы теории вычислимых функций

Основы теории вычислимых функций

Рекурсивные функции

Оценки скорости роста. Функция Аккермана

Вопросы и ответы

Студенты

Авторизоваться

Основы теории вычислимых функций

Основы теории вычислимых функций

Рекурсивные функции

Оценки скорости роста. Функция Аккермана

Вопросы и ответы

Студенты