| Казахстан, Алматы |
Арифметичность вычислимых функций
Программы с конечным числом переменных
Мы хотим показать, что график всякой вычислимой функции является арифметическим множеством, то есть выразим формулой арифметики. Для этого удобно перейти от машин Тьюринга к другой модели, которую можно условно назвать машинами с конечным числом регистров.
Программа для такой машины использует конечное число переменных, значениями которых являются натуральные числа. Числа эти могут быть произвольного размера, так что машина реально имеет память неограниченного объема. Программа состоит из нумерованных по порядку команд. Каждая команда имеет один из следующих видов:
- a:=0
- a:=b
- a:=b+1
- a:=b-1
-
goto
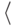 номер
номер 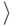
-
if a=0 then goto
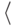 номер1
номер1 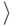 else goto
else goto  номер2
номер2 
- stop
Для тех, кто не сталкивался с командой goto, поясним, что имеется в виду в команде if: если значение переменной a равно нулю, то далее исполняется команда с номером, указанным после then (этот номер конкретное натуральное число, не превосходящее числа команд в программе); если a не равно нулю, то дальше выполняется команда с номером, указанным после else. Команда goto без условия всегда выполняет переход к команде с указанным в ней номером.
Поскольку мы считаем, что значения переменных натуральные (целые неотрицательные) числа, условимся считать разность 0-1 равной 0 (впрочем, это не так важно можно было бы считать это аварией).
Дойдя до команды stop, программа заканчивает работу.
Как и для машин Тьюринга, полезна некоторая практика программирования. Для тренировки напишем программу сложения двух чисел. Она помещает в c сумму чисел, которые были в переменных a и b. Такая программа на паскале имела бы вид
c:=a;
{инвариант: ответ=сумма текущих значений c и b}
while b<>0 do begin
c:=c+1;
b:=b-1;
end;Имитируя цикл с помощью операторов перехода, получаем программу для нашей машины:
1 c:=a 2 if b=0 then goto 6 else goto 3 3 c:=c+1 4 b:=b-1 5 goto 2 6 stop
Теперь легко понять, как написать программы для вычитания, умножения (которое реализуется как цикл с повторным сложением), деления с остатком (как учил еще Энгельс в забытой ныне книге " Диалектика природы", деление есть сокращенное вычитание), возведения в степень, проверки простоты, отыскания n -го простого числа и т.п. Вообще по сравнению с машинами Тьюринга этот язык более привычен и потому легче поверить, что на нем можно запрограммировать все алгоритмы.
Единственное, чего в нем реально не хватает это массивов. Но это легко обойти, поскольку есть числа произвольного
размера и нас не интересует число операций (как это
принято в общей теории алгоритмов). Вместо массива битов мы
можем хранить число, двоичной записью которого он является, а
для массивов чисел воспользоваться, скажем, основной теоремой арифметики и хранить
последовательность 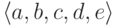 как
число 2a3b5c7d11e. При этом операции a[i]:=b
и b:=a[i] заменяются на небольшие программы, которые
содержат переменные a, b, i и еще несколько
переменных. (Частью этих программ является нахождение простого
числа с заданным порядковым номером.)
как
число 2a3b5c7d11e. При этом операции a[i]:=b
и b:=a[i] заменяются на небольшие программы, которые
содержат переменные a, b, i и еще несколько
переменных. (Частью этих программ является нахождение простого
числа с заданным порядковым номером.)
Легко определить понятие вычислимой (в этой модели) функции. Пусть есть программа с двумя переменными x и y (и, возможно, другими). Поместим в x некоторое число n, а в остальные переменные поместим нули. Запустим программу. Если она не остановится, то вычисляемая ей функция в точке n не определена. Если остановится, то содержимое переменной y после остановки и будет значением функции, вычисляемой нашей программой (в точке n ). Функция называется вычислимой (в этой модели), если существует вычисляющая ее программа.
Как всегда, при определении мы фиксировали различные детали, большинство из которых не являются существенными. Можно было бы добавить некоторые команды (сложение, например) или даже исключить (например, без копирования можно обойтись с помощью небольшой хитрости).
83. Покажите, что класс вычислимых функций не изменится, если исключить из определения команду копирования a:=b.
Несколько более удивительно, что число переменных можно ограничить, скажем, сотней но и это не так уж странно, если вспомнить, что мы можем хранить в одной переменной целый массив.
84. Проверьте это.
Машины Тьюринга и программы
Построенная вычислительная модель не слабее машин Тьюринга в том смысле, что любую вычислимую на машинах Тьюринга функцию можно вычислить и программой с конечным числом переменных.
Теорема 65. Всякая функция, вычислимая на машинах Тьюринга, может быть вычислена с помощью программы описанного вида с конечным числом переменных.
Следует уточнить, однако, что мы имеем в виду, так как для
машин Тьюринга исходное данное и результат были двоичными словами,
а для программ натуральными числами. Мы отождествляем те и другие
по естественному правилу, при котором слова  (пустое), 0, 1, 00, 01,... соответствуют
числам 0, 1, 2, 3, 4 ...(чтобы получить из числа слово, прибавим к
нему единицу, переведем в двоичную систему и отбросим единицу в
старшем разряде).
(пустое), 0, 1, 00, 01,... соответствуют
числам 0, 1, 2, 3, 4 ...(чтобы получить из числа слово, прибавим к
нему единицу, переведем в двоичную систему и отбросим единицу в
старшем разряде).
Как и раньше, мы приведем лишь приблизительное описание того, как по машине Тьюринга строится программа с конечным числом переменных, вычисляющая ту же функцию. Прежде всего конфигурации машины Тьюринга надо закодировать числами. Можно сделать это, например, поставив в соответствие каждой конфигурации четыре числа: номер текущего состояния, номер текущего символа (в ячейке, где стоит головка машины), код содержимого ленты слева от головки и код содержимого ленты справа от головки.
Чтобы решить, как удобнее кодировать содержимое ленты слева и
справа от головки, заметим, что машина Тьюринга обращается с
двумя половинами лентами слева и справа от головки как со стеками. (Стеком называется структура данных, напоминающая
стопку листов. В нее можно положить лист наверх, взять верхний
лист, а также проверить, есть ли еще листы.) В самом деле, при
движении головки направо из правого стека берется верхний
элемент, а в левый стек кладется; при движении налево
наоборот. Стеки легко моделировать с помощью чисел: например,
если в стеке хранятся символы 0 и 1, то добавление
нуля
соответствует операции x 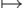 2x, добавление единицы
операции x
2x, добавление единицы
операции x 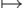 2x+1, верхний элемент есть остаток при
делении на 2, а удаление верхнего элемента есть деление
на 2 (с отбрасыванием остатка). Другими словами, мы воспринимаем
двоичную запись числа как стек, вершина которого находится
справа, у младшего разряда. Точно так же можно использовать n -ичную систему счисления и представить стек с n
возможными
символами в каждой позиции.
2x+1, верхний элемент есть остаток при
делении на 2, а удаление верхнего элемента есть деление
на 2 (с отбрасыванием остатка). Другими словами, мы воспринимаем
двоичную запись числа как стек, вершина которого находится
справа, у младшего разряда. Точно так же можно использовать n -ичную систему счисления и представить стек с n
возможными
символами в каждой позиции.
Теперь основной цикл машины Тьюринга можно записать как программу, оперирующую с указанными четырьмя числами (символ, состояние, левый стек и правый стек) без особых хитростей. Но несколько вещей все-таки надо иметь в виду.
Во-первых, стеки конечны, а лента бесконечна мы должны договориться, что если стек опустошается, то в него автоматически добавляется символ пробела. Тем самым бесконечный пустой хвост ленты может присутствовать в стеке, как теперь говорят, виртуально.
Во-вторых, напомним, что мы договорились отождествлять двоичные слова (которые подаются на вход машины Тьюринга) и их коды (которые хранятся в переменных нашей программы). Поэтому, получив код входного слова, надо его разобрать по символам и положить эти символы один за другим в стек (основания систем счисления разные, так что просто так переписать это нельзя). Аналогичные проблемы возникают и при превращении выхода (части содержимого правого стека) в соответствующее число, но все они легко преодолимы, и мы не будем вдаваться в подробности.
Верно и обратное утверждение:
Теорема 66. Всякая функция, вычислимая программой с конечным числом переменных, вычислима на машине Тьюринга.
Нам надо моделировать поведение программы с помощью машины Тьюринга. Будем считать, что значения переменных записаны на ленте (в двоичной системе) и разделены специальным разделительным символом. Тогда машина может найти любую переменную, идя от начала ленты и считая разделительные символы, сделать что-то с этой переменной и затем вернуться обратно в начало. (Нет необходимости записывать на ленте номер исполняемой команды, поскольку команд конечное число и машина может помнить номер текущей команды как часть своего состояния.) Операции прибавления и вычитания единицы также легко выполнимы в двоичной записи (если идти справа налево). Надо только иметь в виду, что размер числа может увеличиться, и тогда нужно для него освободить место, сдвинув все символы справа от головки на одну позицию. (При уменьшении нужно сдвинуть влево.) Ясно, что это также легко выполнить с помощью машины Тьюринга.
Если мы записываем числа в двоичной системе, то проблемы с перекодированием при вводе-выводе минимальны (надо лишь дописать нули для значений остальных переменных в начале работы и встать в нужное место ленты в конце).
