|
Возможна ли разработка приложения на Octave с GUI? |
Задачи линейной алгебры
5.7 Собственные значения и собственные векторы
Пусть  — матрица размерностью
— матрица размерностью  . Любой ненулевой вектор
. Любой ненулевой вектор  , принадлежащий некоторому векторному пространству, для которого
, принадлежащий некоторому векторному пространству, для которого  , где λ — некоторое число, называется собственным вектором матрицы, а λ — принадлежащим ему или соответствующим ему собственным значением матрицы A.
, где λ — некоторое число, называется собственным вектором матрицы, а λ — принадлежащим ему или соответствующим ему собственным значением матрицы A.
Уравнение  эквивалентно уравнению
эквивалентно уравнению 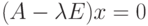 . Это однородная система линейных уравнений, нетривиальные решения которой являются искомыми собственными векторами. Она имеет нетривиальные решения только тогда, когда
. Это однородная система линейных уравнений, нетривиальные решения которой являются искомыми собственными векторами. Она имеет нетривиальные решения только тогда, когда  , то есть, если
, то есть, если 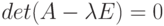 . Многочлен
. Многочлен  называется характеристическим многочленом матрицы A, а уравнение
называется характеристическим многочленом матрицы A, а уравнение 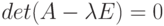 — характеристическим уравнением матрицы A. Если
— характеристическим уравнением матрицы A. Если 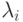 — собственные значения
— собственные значения  , то нетривиальные решения однородной системы линейных уравнений
, то нетривиальные решения однородной системы линейных уравнений 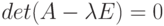 есть собственные векторы A, принадлежащие собственному значению
есть собственные векторы A, принадлежащие собственному значению 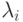 . Множество решений этой системы уравнений называют собственным подпространством матрицы A, принадлежащим собственному значению
. Множество решений этой системы уравнений называют собственным подпространством матрицы A, принадлежащим собственному значению 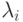 , каждый ненулевой вектор собственного подпространства является собственным вектором матрицы A.
, каждый ненулевой вектор собственного подпространства является собственным вектором матрицы A.
Иногда требуется найти собственные векторы y и собственные значения 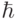 , определяемые соотношением
, определяемые соотношением 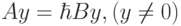 , где
, где  — невырожденная матрица. Векторы
— невырожденная матрица. Векторы  и числа
и числа 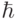 обязательно являются собственными векторами и собственными значениями матрицы
обязательно являются собственными векторами и собственными значениями матрицы 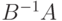 .
Пусть
.
Пусть 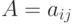 и
и 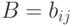 , причём матрица
, причём матрица  является положительно определённой, тогда собственные значения
является положительно определённой, тогда собственные значения 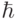 совпадают с корнями уравнения
совпадают с корнями уравнения  –й степени
–й степени 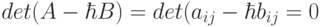 . Это уравнение называют характеристическим уравнением для обобщённой задачи о собственных значениях. Для каждого корня
. Это уравнение называют характеристическим уравнением для обобщённой задачи о собственных значениях. Для каждого корня 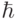 кратности
кратности  существует ровно
существует ровно  линейно независимых собственных векторов
линейно независимых собственных векторов  .
.
Пример 5.14. Найти собственные значения и собственные векторы матрицы  .
.
В листинге 5.15 показано решение поставленной задачи.
disp( ’Введите матрицу:’ ); A=input ( ’A=’ ); [ n,m]= size (A); disp( ’Вектор собственных значений матрицы A:’ ); d=eig (A) [ L, D]= eigA); disp( ’L - Матрица собственных векторов:’ ); L disp( ’D - Диагональная матрица собственных значений:’ ); D disp( ’Проверка:’ ); for i =1:n (A - D( i, i ) * eye ( n ) ) *L ( :, i ) end; % _____________________________________ Введите матрицу: A= [ 5 2 -1;1 -3 2; 4 5 -3] Вектор собственных значений матрицы A: d = 4.9083e+00 -2.1495e-16 -5.9083e+00 L - Матрица собственных векторов: L = -0.796113 -0.049326 0.181303 -0.241044 0.542590 -0.598803 -0.555069 0.838548 0.780106 D - Диагональная матрица собственных значений: D = Diagonal Matrix 4.9083e+00 0 0 0 -2.1495e-16 0 0 0 -5.9083e+00 Проверка: ans = -2.3657e-16 -4.3585e-16 7.4420e-16 ans = 2.7756e-17 -4.1633e-16 4.4409e-16 ans = 2.0632e-16 1.5772e-15 2.6606e-16Листинг 5.15. Нахождение собственных значений (пример 5.14).
Пример 5.15. Привести заданную матрицу к диагональному виду.
Задача состоит в том, чтобы для квадратной матрицы  подобрать такую матрицу
подобрать такую матрицу  , чтобы матрица
, чтобы матрица  имела диагональный вид. Эта задача связана с теорией собственных значений, так как разрешима только в том случае, если матрица
имела диагональный вид. Эта задача связана с теорией собственных значений, так как разрешима только в том случае, если матрица  состоит из собственных векторов матрицы
состоит из собственных векторов матрицы  .
.
В листинге 5.16 приведено решение поставленной задачи.
disp( ’Введите матрицу:’ ); A=input ( ’A=’ );
format bank;
[ C,D]= eig (A);
disp( ’Диагональная матрица к матрице А:’ ); D
disp( ’Проверка B=D’ ); B=inv (C) *A*C
% _____________________________________
Введите матрицу:
A= [ 2 1 3; 1 -2 1; 3 2 2 ]
Диагональная матрица к матрице А:
D =
Diagonal Matrix
5.41 0 0
0 -1.00 0
0 0 -2.41
Проверка B=D
B =
5.41 -0.00 -0.00
0.00 -1.00 0.00
-0.00 -0.00 -2.41
Листинг
5.16.
Приведение к диагональному виду (пример 5.15).
Пример 5.16. Найти решение обобщённой задачи о собственных значениях для матриц  и
и  .
.
Обобщённую задачу о собственных значениях (листинг 5.17) решают при помощи функции 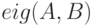 , которая в качестве результата выдаёт матрицу обобщённых собственные векторов и диагональную матрицу, содержащую обобщённые собственные значения.
, которая в качестве результата выдаёт матрицу обобщённых собственные векторов и диагональную матрицу, содержащую обобщённые собственные значения.
disp( ’Введите матрицу А:’ ); A=input ( ’A=’ ); disp( ’Введите матрицу В:’ ); B=input ( ’B=’ ); [ X,V]= eig (A,B); disp( ’Матрица обобщённых собственных векторов:’ ); X disp( ’Матрица обобщённых собственных значений:’ ); V disp( ’Обобщённые собственные значения:’ ); v=diag (V) % _____________________________________ Введите матрицу А: A= [ 1 -3;-3 4 ] Введите матрицу В: B= [ 1 2; -3 1 ] Матрица обобщённых собственных векторов: X = 1.00 0.92 0.00 1.00 Матрица, содержащая обобщённые собственные значения: V = Diagonal Matrix 1.00 0 0 -0.71 Обобщённые собственные значения: v = 1.00 -0.71Листинг 5.17. Обобщённая задача о собственных значениях (пр. 5.16).
5.8 Норма и число обусловленности матрицы
Матричная норма — это некоторая скалярная числовая характеристика, которую ставят в соответствие матрице. В задачах линейной алгебры используются различные матричные нормы:
- первая норма
 квадратной матрицы
квадратной матрицы  :
:
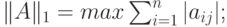
- вторая норма
 квадратной матрицы
квадратной матрицы  :
: , где
, где 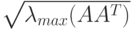 — максимальное собственное значение матрицы
— максимальное собственное значение матрицы  ;
; - евклидова норма
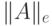 квадратной матрицы
квадратной матрицы  :
: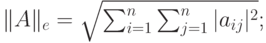
- бесконечная норма
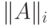 квадратной матрицы
квадратной матрицы  :
: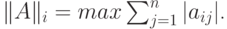
Число обусловленности матрицы A используется для определения меры чувствительности системы линейных уравнений 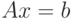 к погрешностям задания вектора
к погрешностям задания вектора  . Чем больше число обусловленности, тем более неустойчив процесс нахождения решения системы. Существует несколько вариантов вычисления числа обусловленности, но все они связаны с нормой матрицы, и равны произведению нормы исходной матрицы на норму обратной:
. Чем больше число обусловленности, тем более неустойчив процесс нахождения решения системы. Существует несколько вариантов вычисления числа обусловленности, но все они связаны с нормой матрицы, и равны произведению нормы исходной матрицы на норму обратной:
- число обусловленности матрицы, вычисленное в норме
 ;
; - число обусловленности матрицы, вычисленное в норме
 ;
; - число обусловленности матрицы, вычисленное в норме
 ;
; - число обусловленности матрицы, вычисленное в норме
 .
.
Пример 5.17. Вычислить нормы и числа обусловленности матрицы A.
В листинге 5.18 приведён фрагмент документа, в котором происходит вычисление норм матрицы A с помощью функции  и по соответствующим формулам. Вычисление чисел обусловленности проведено при помощи функции
и по соответствующим формулам. Вычисление чисел обусловленности проведено при помощи функции  и по формулам, отражающим зависимость числа обусловленности от соответствующей нормы матрицы.
и по формулам, отражающим зависимость числа обусловленности от соответствующей нормы матрицы.
disp( ’Введите матрицу:’ ); A=input ( ’A=’ ); [ n,m]= size (A); disp( ’Первая норма:’ ); n_1= norm(A, 1 ) N_1= max(sum( abs (A) ) ) disp ( ’Вторая норма:’ ); n_2= norm(A, 2 ) N_2= sqrt(max( eig (A*A’ ) ) ) disp( ’Бесконечная норма:’ ); n_i= norm(A, inf ) N_i= max(sum( abs (A’ ) ) ) disp( ’Евклидова норма:’ ); n_e= norm(A, ’fro’ ) N_e= sqrt(sum( diag (A*A’ ) ) ) disp( ’Число обусловленности в первой норме:’ ); c_1= cond (A, 1 ) C_1= norm(A, 1 ) *norm( inv (A), 1 ) disp ( ’Число обусловленности во второй норме:’ ); c_2= cond (A, 2 ) C_2= norm(A, 2 ) *norm( inv (A), 2 ) disp ( ’Число обусловленности в бесконечной норме:’ ); c_i= cond (A, inf ) C_i= norm(A, inf ) *norm( inv (A), inf ) disp ( ’Число обусловленности в евклидовой норме:’ ); c_e= cond (A, ’fro’ ) C_e= norm(A, ’fro’ ) *norm( inv (A), ’fro’ ) % _____________________________________ Введите матрицу: A= [ 5 7 6 5; 7 10 8 7; 6 8 10 9; 5 7 9 10 ] Первая норма: n_1 = 33.00 N_1 = 33.00 Вторая норма: n_2 = 30.29 N_2 = 30.29 Бесконечная норма: n_i = 33.00 N_i = 33.00 Евклидова норма: n_e = 30.55 N_e = 30.55 Число обусловленности в первой норме: c_1 = 4488.00 C_1 = 4488.00 Число обусловленности во второй норме: c_2 = 2984.09 C_2 = 2984.09 Число обусловленности в бесконечной норме: c_i = 4488.00 C_i = 4488.00 Число обусловленности в евклидовой норме: c_e = 3009.58 C_e = 3009.58Листинг 5.18. Вычисление матричных норм (пример 5.17).

